我国历年造林面积与林业投入的协整分析
2012-07-10黄文学泽桑梓
黄文学,刘 凌,季 梅 ,泽桑梓
(1.习水县林业局,贵州 习水 564600;2.云南省林业科学院,云南 昆明 650201)
林业是重要的公益事业和基础产业,也是保护生态环境、促进经济社会可持续发展的重要基础[1]。目前,我国仍然是一个林业资源缺乏的国家,森林资源总量严重不足,森林生态系统的整体功能非常脆弱[2]。“十一五”以来,国家通过一系列措施,加大对林业经济的支持,使得森林覆盖率逐步提升,林业产值也逐渐提高,生态环境也开始改善[3]。
我国的林业投入包括很多方面,其中包括扩大造林面积和发展林业产业等,扩大造林面积对改善我国生态环境有直接的影响[4]。林业投入与造林面积的关系如何,研究通过提取我国林业统计数据,对我国历年林业投入与造林面积的增长关系进行协整分析,并对协整分析结果进行格兰杰因果检验,为进一步提高林业投入效益提供参考。
1 材料与方法
1.1 材料
采用1991~2009年我国历年造林面积(AREA)和林业投入(INPUT)的年度数据为样本。为消除数据中存在的异方差,分别对数据样本取对数,即LOG AREA和LOGINPUT,数据见表1。历年造林面积和林业投入原始数据来源于中国林业统计年鉴2004、2010 等[5-7]。
1.2 方法
协整分析是用于检验两组随时间波动变化的非平稳变量在长期内是否具有稳定关系。可分为两种:一种是基于回归残差的EG两步法协整检验;另一种是基于回归系数的乔根森检验[8]。
试验使用EG法对LAREA和LINPUT两组变量间的关系进行检验。EG两步法协整检验是通过对同阶单整变量用一个变量对另一个变量进行回归求得残差序列,然后检验其平稳性,若残差序列平稳,说明变量间存在协整关系,否则,就不存在协整关系。如果具有协整关系,再对具有协整关系的时间变量序列的因果关系进—步检验分析。
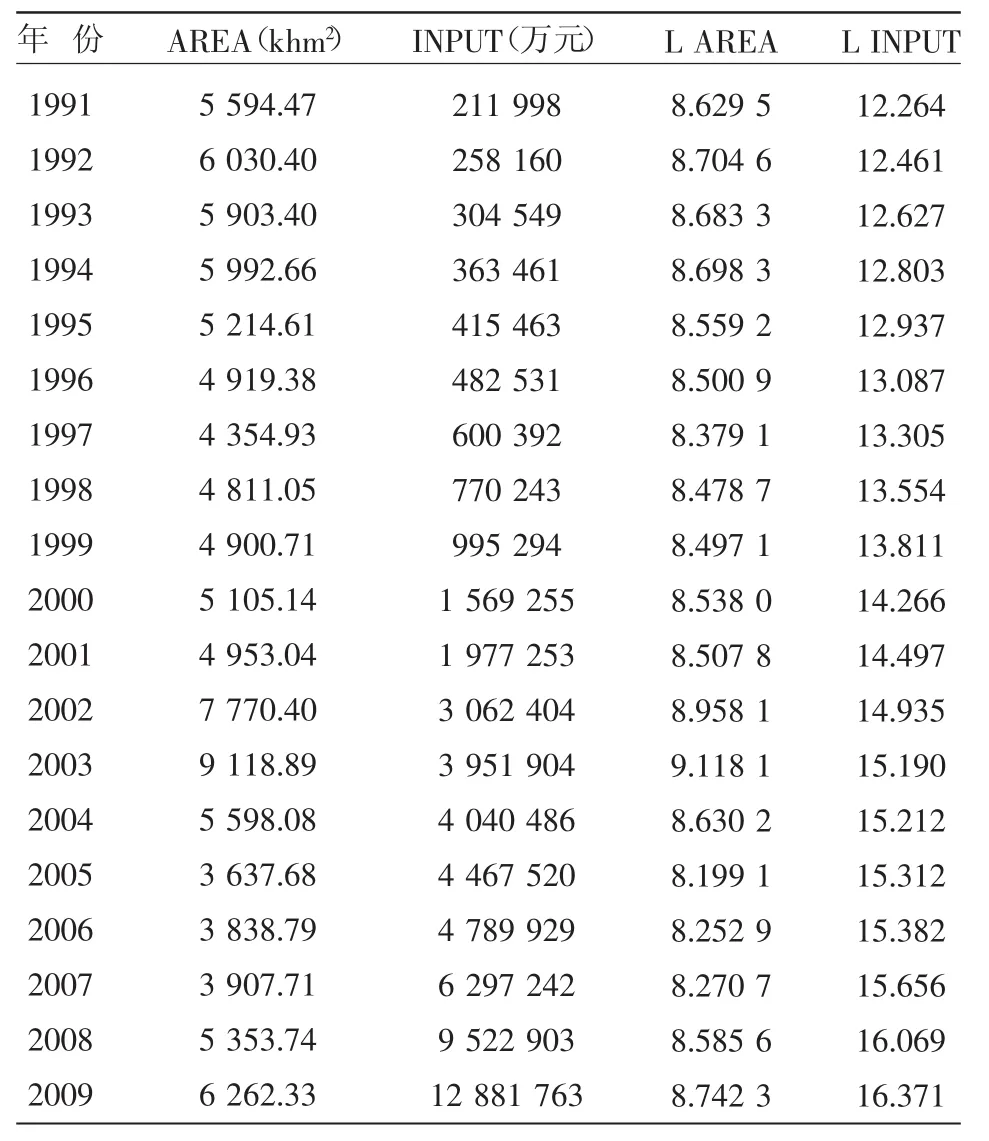
表1 我国历年造林面积(AREA)和林业投入量(INPUT)
试验利用EViews5.0分析软件进行协整分析[9]。
1.2.1 变量平稳性检验 时间变量必须为平稳序列,否则会出现“虚假回归”。因此,在协整检验之前,要对变量进行平稳性检验。用EViews5.0对变量LAREA和LINPUT进行ADF平稳性检验,确定两组变量是否是平稳序列。
1.2.2 协整检验 协整检验是揭示两组变量是否为长期稳定的均衡关系的方法,如果LAREA和LINPUT两组变量存在平稳性,用EViews5.0对序列进行回归分析,确定回归方程;第二步是对回归方程的残差进行单位根检验,若残差不存在单位根,那么所得到的回归方程就是变量之间的协整方程,否则就不是。
1.2.3 误差修正模型 假如LAREA和LINPUT两组变量之间存在长期均衡关系,但在短期内,这些变量可以是不均衡的。Granger表述定理称一组具有协整关系的变量短期非均衡关系一定有一个误差修正模型来表述[10]。建立误差修正模型可以分析它们之间的短期动态均衡关系。笔者利用EG两步法估计相应参数,得到误差修正模型。
1.2.4 格兰杰因果检验 Granger指出,如果变量X有助于预测变量Y,即根据Y的过去值对Y进行自回归时,如果再加上X的过去值,能显著地增强回归的解释能力,则称X是Y的格兰杰原因,否则,称为非格兰杰原因[11]。协整检验能够确定两组变量的联系程度,但不能体现两组变量是否相互影响,因此需要进行格兰杰因果检验。
如果LAREA和LINPUT两组变量具有平稳性,则利用EViews5.0软件对这两组变量进行格兰杰因果检验。
2 结果与分析
2.1 变量平稳性检验
采取最常用的ADF平稳性检验来判断2组变量的平稳性,检验结果见表2、表3、表4。从表2、表3中可以看出,在5%的置信区间下,2个变量的水平序列和其一阶差分序列都是不平稳的。从表4可以看出,在1%和5%的置信区间下,变量二阶差分的ADF值都大于临界值,因此2组变量的水平序列不存在单位根,是平稳序列。
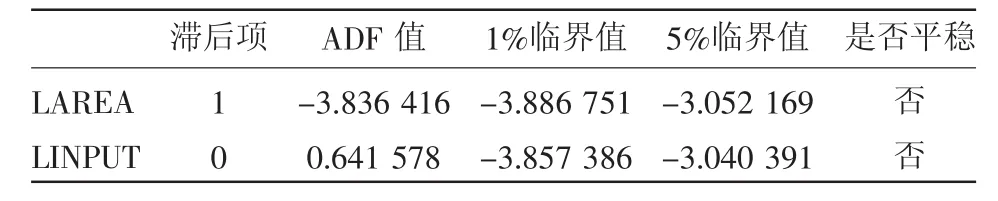
表2 变量的ADF单位根检验结果
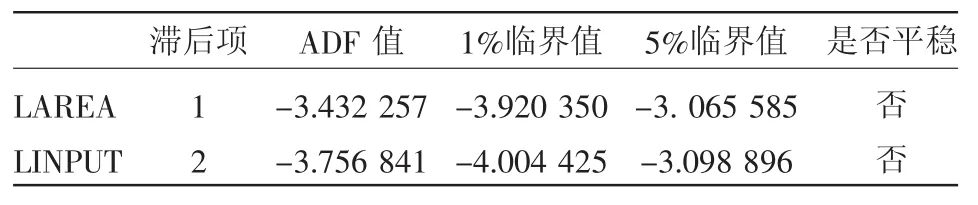
表3 变量一阶差分的ADF单位根检验结果
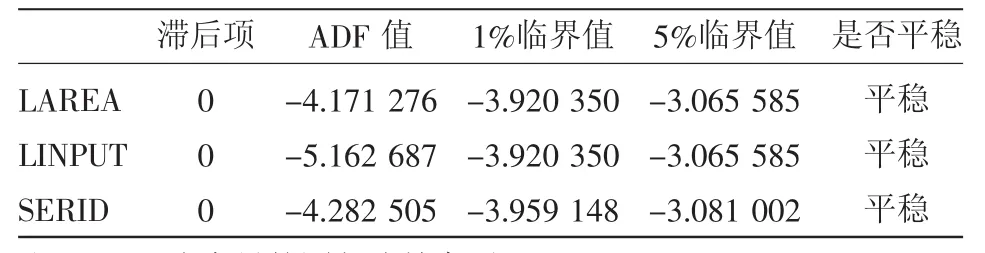
表4 变量二阶差分的ADF单位根检验结果
2.2 协整检验
通过2.1的变量平稳性检验,认为两变量LAREA和LINPUT的水平序列是平稳序列,满足协整检验前提。
用EG两步法对LAREA和LINPUT两变量进行协整关系检验,即计算两变量的回归方程和检验回归残差项e是否为平稳序列。回归残差项e的ADF检验值-4.171 276小于显著性水平为1%、5%时的临界值(-3.920 350和-3.065 585),拒绝原假设,即残差序列e是平稳,见表4。结果显示变量LAREA和LINPUT之间存在(2,2)阶协整关系。
2.3 误差修正模型
通过建立误差修正模型来研究各变量之间关系的短期动态调整与长期特征。误差修正模型分析结果见表5。
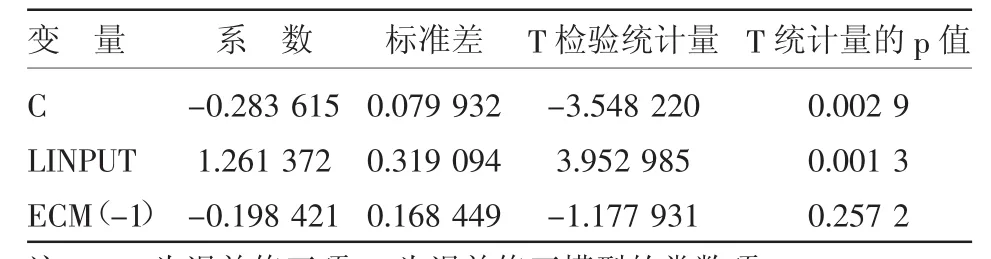
表5 误差修正模型结果表
其误差修正模型为:
DLAREA=-0.283 6148 393+1.261 372 341×DLINPUT-0.198 421 123 5×E(-1)
由表5可知,LAREA和LINPUT的误差修正模型的误差修正系数(-0.198 421)小于零,符合反向修正原则。LAREA和LINPUT的误差修正系数的绝对值较小,说明当它们偏离均衡趋势后的回调速度较小,这2个变量的波动也较小。
2.4 格兰杰因果检验
由协整检验结果可知,历年造林面积和林业投入之间存在长期的均衡关系,但这种均衡关系是否是因果关系还需进行因果关系检验。
借助Eviews5.0软件,进一步研究变量LAREA和LINPUT是否具有格兰杰因果关系。结果见表6。根据表6的检验结果,由于p值小于0.05就是有因果关系,因此,从2阶滞后的情况来看,LAREA和LINPUT之间只存在单方面的因果关系:LINPUT在1%的显著水平上不是LAREA的原因,LAREA在1%的显著水平上是LINPUT的原因。由此可知,在样本区间内,林业投入影响历年造林面积的程度较小,历年造林面积的增长能促使林业投入的增长。

表6 格兰杰因果关系检验结果
3 结 论
对1991~2009年统计数据的实证分析可知,从长期关系来看,我国历年造林面积和林业投入之间存在长期稳定的均衡关系,历年造林面积的增长促使了林业投入的增加,历年造林面积和林业投入之间只存在单向的Granger因果关系,我国历年造林面积的增长是林业投入增长的原因。从短期关系来看,林业投入的变化可以引起历年造林面积的同方向变化[12]。林业投入对历年造林面积的增长有显著推动作用,我国应加大林业投入,以推动历年造林面积的增长,加快我国的国土绿化工程,改善我国生态环境,促进林业可持续发展。
试验只是简要分析了我国历年造林面积和林业投入之间的关系,对影响我国历年造林面积的其它因素未作分析,在下一步研究中,应该将国家退耕还林的成果、防护林的建设等因素结合起来,定量研究各种因素与历年造林面积的关系,更好地掌握我国林业的发展动态。
[1]国家林业局.中国林业年鉴2009[M].北京:中国林业出版社,2010.
[2]张文涛,严 耕.中国林业史学发展史研究述论[J].安徽农业科学,2011,39(17):10291-10293.
[3]彭行荣.现代林业与我国林业的发展战略[J].湖北农业科学,2010,49(7):1783-1786.
[4]刘 燕.市场经济下增加林业投入的对策[J].西北农林科技大学学报(社会科学版),2001,1(3):50-52.
[5]国家林业局.中国林业统计年鉴2004[M].北京:中国林业出版社,2005.
[6]国家林业局.中国林业统计年鉴2010[M].北京:中国林业出版社,2011.
[7]张煜星.人工造林对森林覆盖率的贡献分析[J].东北林业大学学报,2007,35(3):76-79.
[8]杨丹萍.宁波对外贸易与经济增长关系的协整分析[J].宁波大学学报(理工版),21(3):438-441.
[9]樊欢欢.Eviews统计分析与应用 [M].北京:机械工业出版社,2009.
[10]李亚明,佟仁城.中国房地产财富效应的协整分析和误差修正模型[J].系统工程理论与实践,2007,(11):1-6,33.
[11]朱慧明,韩玉启.产业结构与经济增长关系的实证分析[J].运筹与管理,2003,12(2):68-72.
[12]梅付春.河南省林业生态建设模式探讨[J].内蒙古农业科技,2011,(5):4-6.
