关于不定方程x2 +16 =y13 的解

杨 全

(商洛学院 数学与计算科学系，陕西 商洛726000)

的解的讨论是数论中的一类重要课题. 当A = 1，B = 1 时，LEDESGUE［1］证明了式(1)无整数解.NAGELL［2］证明了当A=2，B=1，n=5 时，式(1)仅有整数解(x，y)=(±11，3).对于A =1，B =16，n =3，5，7，11 时的情况均已讨论过［3－6］，而对于当A=1，B =16，n =13 时的情况未曾讨论.因此，本文讨论了当A=1，B=16，n=13 时的情况，给出了如下的定理.

定理 不定方程

无整数解.

1 引理

引理［7］设M 是惟一分解整数环，正整数k ≥2，以及那么，若则有

其中，ε1，ε2是M 中的单位元素，并且ε1ε2= εk，ε 为单位元素.

2 定理的证明

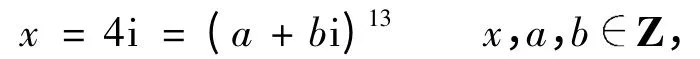
因而有

因此b = ±1，±2，±4.当b = 1 时，由式(4)可得

当b = －1 时，由式(4)可得

故当x ≡1(mod 2)时，式(2)无整数解.

下面讨论x ≢1(mod 2)的情况，容易知道y 也为偶数，令此时式(2)变为

即

易知x1必为偶数，从而y1也为偶数.再令x1= 2x2，y1= 2y2，x2，y2Z，此时式(5)变为

易知x2必为奇数，在Z中式(6)可以写成

设(x2+i，x2－i)= d，则d| (2x2，2i)即d| 2，从而d = 1，1 －i，2.若d = 1，则－［(1 －i)4］11一定只能整除x2+i 或x2－i 中的一个，则有

即411但x2为奇数，则此式不成立.所以d ≠1.同理d = 1 －i 也是不正确的.故d = 2，此时式(6)可化为

故由引理可得

因而有

显然式(8)是不成立的.故当x ≢1(mod 2)时，式(2)无整数解.

综上所述，不定方程x2+16 = y13无整数解.定理证毕.

［1］LEBESGUE V A.Surlimpossibilite en nombers entiers de equation xm=y2+1［J］.Nouv Amn.Math，1850，9(1):178－181.

［2］NAGELL T. Surlimpossibilite de quelques equations deux indeterminees［J］.Norsk Marem.Forenings Skrifter，Senel，1921，13:65－82.

［3］廖江东，柳杨.关于不定方程x2+16 =y3［J］.四川理工学院学报:自然科学版，2007，20(2):4 －5.

［4］黄勇庆，柳杨. 关于不定方程x2+16 =y5［J］.乐山师范学院学报，2006，21(12):10 －11.

［5］高丽，马永刚. 关于不定方程x2+16 =y7的解的讨论［J］.西南民族大学学报:自然科学版，2008，34(1):27 －29.

［6］李中恢，张四保. 关于不定方程x2+16 =y11的解［J］.海南大学学报:自然科学版，2009，27(3):216 －218.

［7］潘承洞，潘承彪.代数数论［M］.济南:山东大学出版社，2003.

［8］潘承洞，潘承彪.初等数论［M］.北京:北京大学出版社，1992.