Sturm－Liouville 算子特征值与特征函数的精确解①

陈莉敏

(常州工程职业技术学院基础部，江苏常州213164)

1 引言及预备知识

对于Sturm－Liouville特征值问题Ly(x)=－y″+q(x)y=λy，y'(0)－hy(0)=0，y'(π)+Hy(π)=0，若q(x)∈Cm[0，π]，则特征值渐近式可表示为:

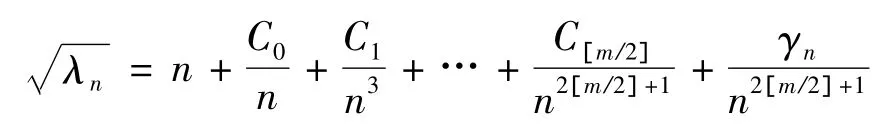
其中是与h，H，q(x)及其导数相关的实常数[1，2]．

当势函数光滑性提高时，会得到更精确的渐近式的表达式．但如何得到这些估计式中的系数确切表达式，没有文献进行过具体的讨论．本文就是利用迭代法求解当q(x)∈C2[0，π]时算子特征值和特征函数的渐近展开式．

引理 1[3]记 λ=s2，则

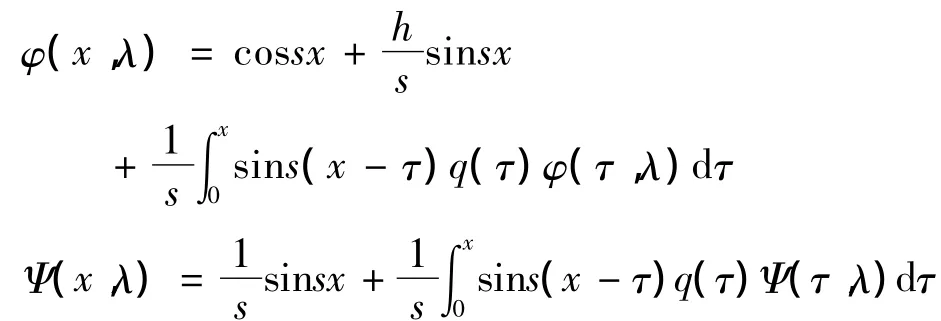
引理2[3]记s=σ+it，则存在s0＞0，使得当|s|＞s0时有 φ(x，λ)=O(e|t|x)，Ψ(x，λ)=，或者更准确些 φ(x，λ)=cossx+，这些估计式对x∈[0，π]一致成立．

定理1[3]自伴边条件下的特征值都是实的．

2 主要结果及其证明

定理2 Sturm－Liouville算子在q(x)∈C2[0，π]时，特征值的渐近展开式中系数C0和C1为:证明: 当h=∞，H≠∞时，由定理1及引理

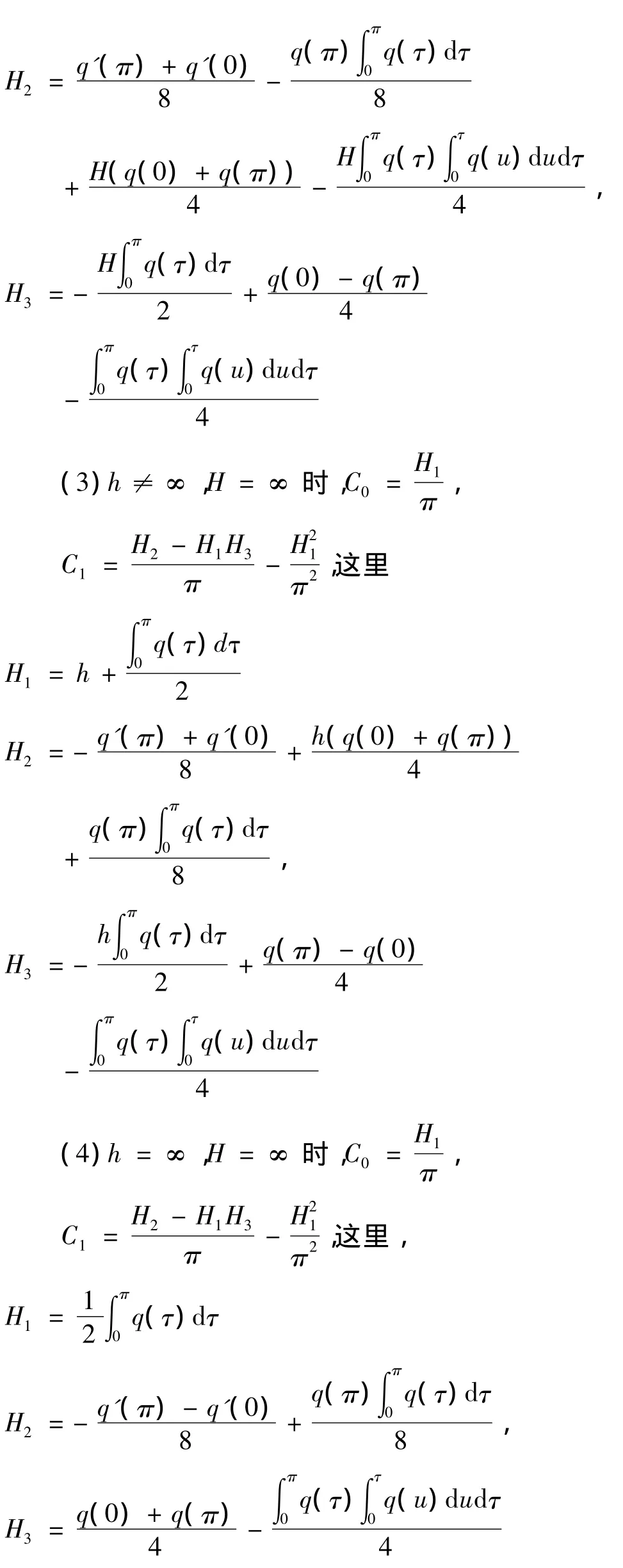
2递推可得．

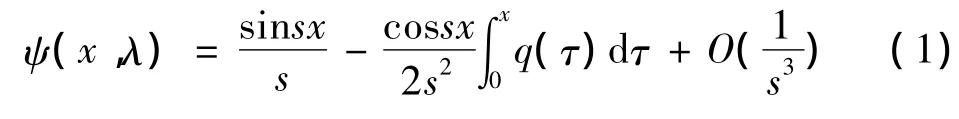
由边条件得:

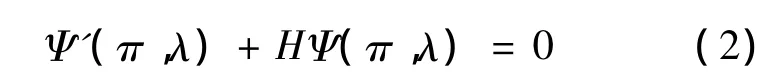
将(1)带入(2)得

对于其他边条件，同理可证．

定理3 Sturm－Liouville算子在q(x)∈C2[0，π]时，特征函数的渐近式可表示为:

(1)h≠∞，H≠∞ 时，

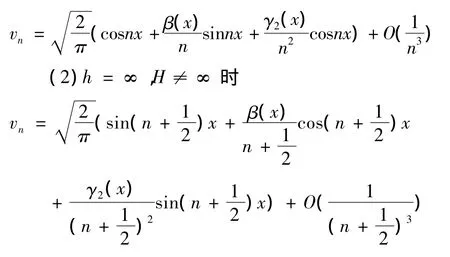
(3)h≠∞，H=∞ 时，

其中β(x)，γ2(x)是与h，H，q(x)及其导数相关的实常数．

证明: 当h≠∞，H≠∞时，由定理1及引理2递推可得，

将定理2相应结论代入(5)式得

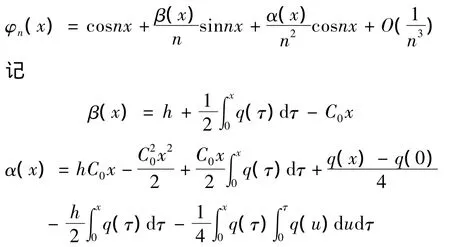
将φn(x)规范化:

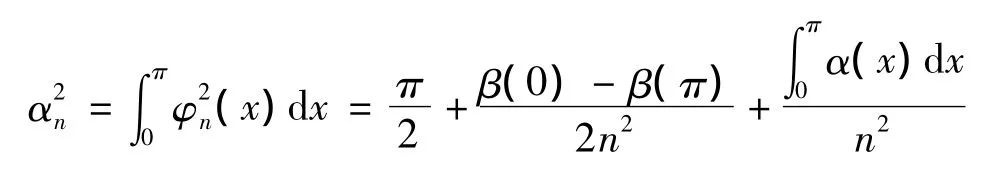
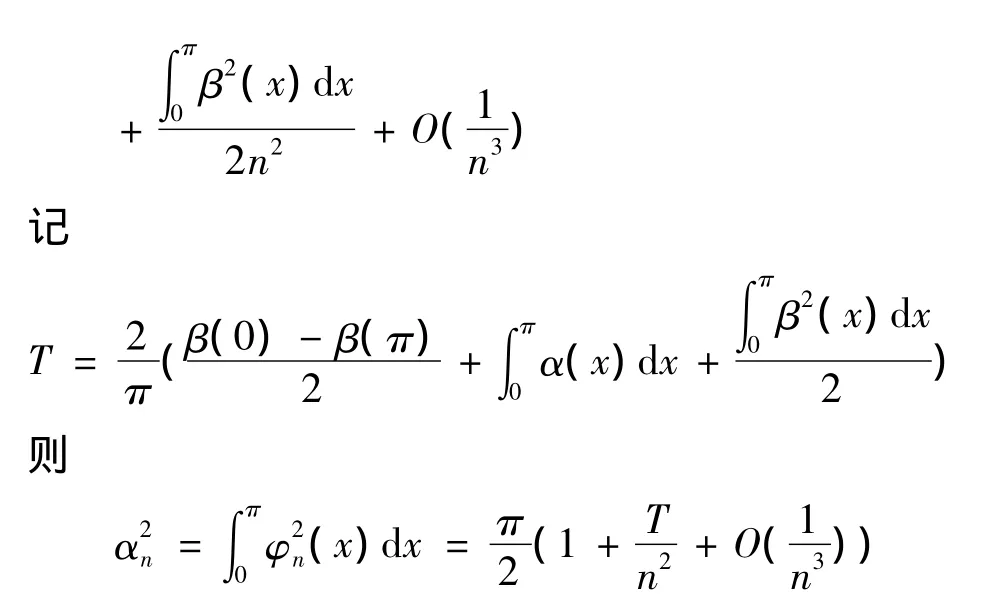
这样

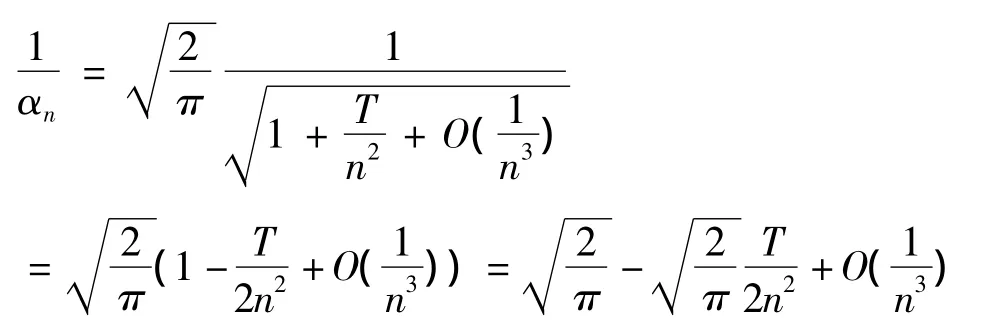
所以规范化了的特征函数有渐近式:

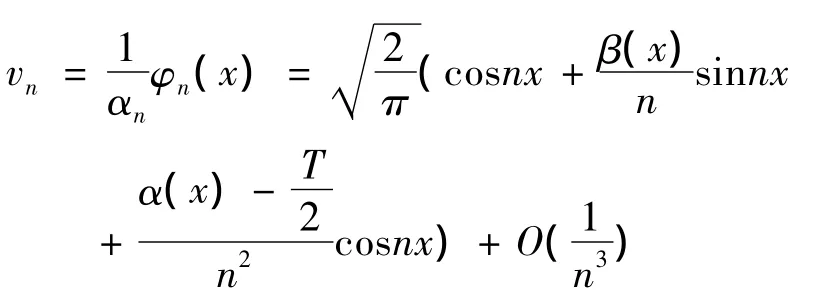
对于其他边条件同理可证．

[1] Atknson FV．Discrete and Continuous Boundary Problems[M]．New York:Academic Press，1964．

[2] Easthamm SP．On the Location of Spectral Concentration for Sturm － Liouville Problems with Rapidly Decaying Potential[J]．Mathematica，1998，45:23 －36．

[3] 刘景麟．常微分算子谱论[M]．北京:科学出版社，2009．

[4] Levitan BM，Sargsjan IS．Sturm－Liouville and Dirac Operators[M]．Kluwer Academic Publishers，1991．