随机利率下多元衰减模型的Thiele’s 微分方程①

许道军， 李 敏， 沈 浮

(解放军陆军军官学院基础部数学教研室，安徽合肥230031)

0 引言

不管是单张保单还是保单组合，死亡率和利率都随机时准备金的表达形式比较繁琐，因此，人们对随机利率下寿险的准备金理论研究很少，对于多元衰减模型的情形更是如此．在Hans U．Gerber的著作“Life Insurance Mathematics”(Third Edition 1997)中给出了在固定利息力δ下多元衰减的模型

(1)在时刻t，由第j种原因导致死亡的保险金额记为Cj(t)，(j=1，2，…，m);

(2)在时刻t，由第j种原因导致死亡的死亡力函数记为 μj，x+t，(j=1，2，…，m)，且有

(3)保费连续缴纳，设时刻t的保费缴纳率为π(t)的净准备金与Thiele’s微分方程，得到时刻t缴纳的保费由储蓄保费πs(t)和(死亡)风险保费πr(t)构成，其中 πs(t)

1 模型的建立

亡后立即给付，采用下面的表示方法

(1)在时刻t，由第j种原因导致死亡的保险金额记为Cj(t)，j=1，2，…，m;

(2)在时刻t，由第j种原因导致死亡的死亡力

考虑下面的模型:在x岁投保的寿险，假设保费连续缴纳，死亡原因有m种，死亡保险金额在死函数记为μj，x+t，j=1，2，…，m，且有

(3)保费连续缴纳，设时刻t的保费缴纳率为π(t);

(4)在时刻t的利息力函数随机变量记为，其中t≥0，δ≥0，β 为参数，W(t)为标准Wiener过程．

3 论文必须包括题名(不超过20个汉字)、作者姓名(多位作者的署名之间以逗号“，”隔开，不同工作单位的作者，应在姓名右上角加注阿拉伯数字序号)、作者工作单位(写明地址、邮政编码和联系电话，并在其工作单位名称之前加与作者姓名序号相同的数字，各工作单位之间连排并以分号“；”隔开)、中文摘要(100-200字)、关键词(3-5个)、中图分类号、英文题目、作者姓名(汉语拼音)及英译作者单位、英文摘要及关键词、正文、参考文献。

记Y(t)，易得Y(t)，时刻t保险人的未来损失量为

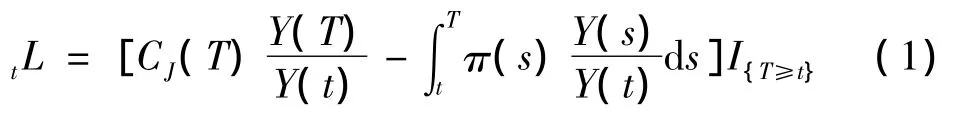
2 净准备金与Thiele’s微分方程

定理1: 时刻t的净准备金

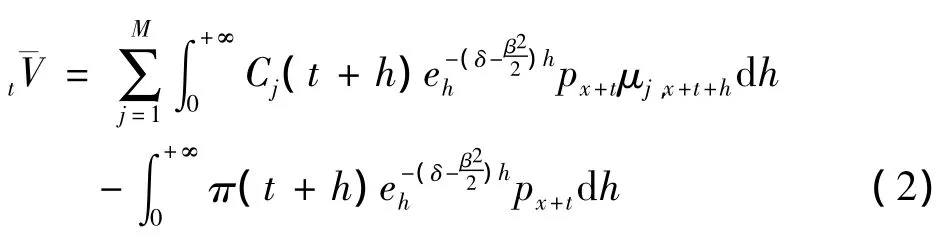
证明: 由净准备金的定义知，时刻t的净准备金

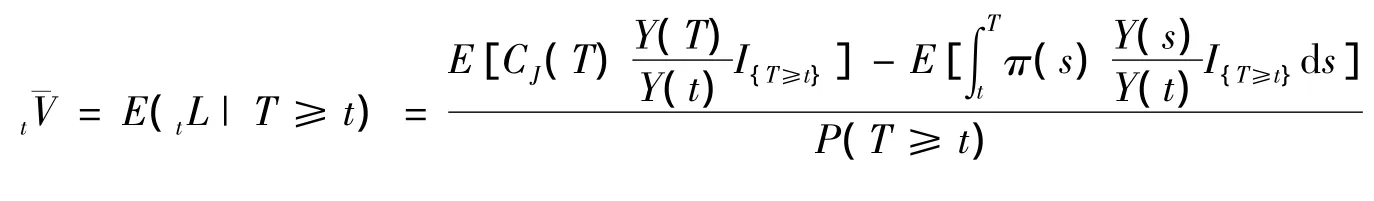
定理2: 时刻t的净准备金t对t的导数

从而有

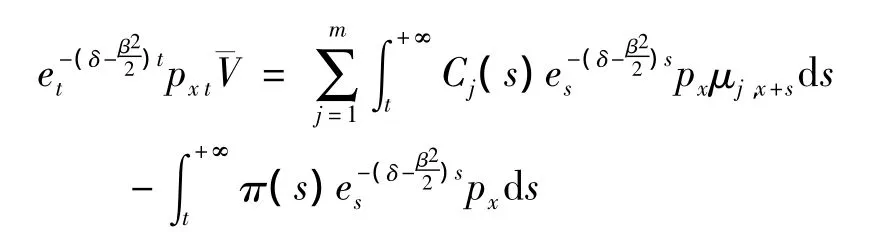
方程两边t求导数，得到

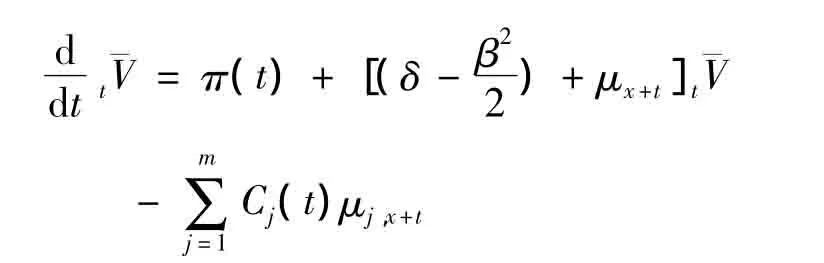
显然，(3)式就是随机利率为Wiener过程时的Thiele’s Differential Equation．值得注意的是，它与固定利率下的Thiele’s Differential Equation在结构上是一致的．(3)式整理得

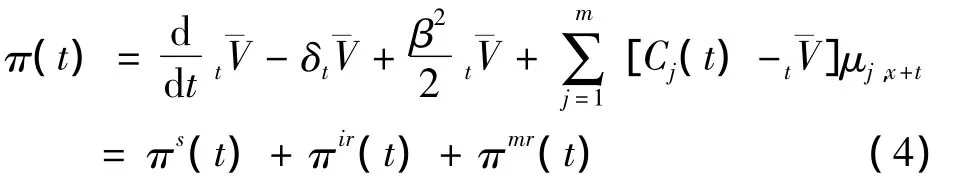
这里，πs(t)为储蓄保费，而πir(t)为利率风险保费，πmr(t)为死亡风险保费，因此在随机利率条件下，风险保费是由利率风险保费和死亡风险保费两部分组成，即

证明: 在定理1的证明中，易知πr(t)=πir(t)+πmr(t)

不难发现，随机利率下的保费比固定利率下多出一部分，即利率风险保费πir(t)，而在传统的固定利率的情形下，这一部分保费全部是由保险公司独自承担的，这必然加大了保险公司的经营风险．

3 数值模拟

下面，将把固定利率下多元衰减模型的净准备金与随机利率下的多元衰减模型的净准备金进行数值模拟并比较．假定衰减原因有两种，即m=2，并设两种原因导致的死亡保险金额分别为:C1(t)=1000，C2(t)=2000，两种原因导致死亡的死亡力分别为:μ1，x=，投保年龄x=25，极限年龄ω=105，保费缴纳率π(t)取常数．

在传统的固定利率下，假设利息力δ=0．05，则由0V=0，计算出保费缴纳率π(t)=73．0240．在随机利率为Wiener过程下，取δ=0．05，β=0．1，仍由0V=0，计算出保费缴纳率 π(t)=73．6495．

通过两种模型的对比，首先在随机利率下，保费缴纳率π(t)=73．6495，要比固定利率下的保费缴纳率π(t)=73．0240增加了0．6255．不难发现，这正是由于利率风险的存在所导致的，所以按照固定利率收取保费，实际上增大了保险公司的经营风险．其次，当β=0．1时，刚开始时，利率风险保费πir(t)的值都比较小，当然这首先是由保额较低所导致的，但是可以看到πir(t)随着t的增加也在不断增加．事实上，随着投保人年龄的增大，保险公司的准备金也会随之大幅增长，从而导致利率风险保费的增加，由Matlab容易计算出当t=50时，利率风险保费高达7．0250，约占保费的10%，因此保险公司在实际经营中利率风险是绝对不容忽视的，在产品设计中，不应忽视利率风险保费的收取．

[1] Hans U．Gerber．Life Insurance Mathematics[M]．Springer，1997，75 －81．

[2] 杨静平．寿险精算基础[M]．北京:北京大学出版社，2002．

[3] Kellison S G．尚汉冀，译．利息理论[M]．上海:上海科学技术出版社，1995．

[4] 张千祥．一类随机利率模型下的年金计算问题[J]．巢湖学院学报，2006，(3):1 －2．

[5] 尚勤，王永茂．随机利率下的年金[J]．吉林师范大学学报，2004，(3):49 －51．

[6] 王廷臣，代金，张波．随机利率下的保险精算函数[J]．经济数学，2004(3):189－193．