带负顾客和Bernoulli 反馈的M/G/1休假排队系统①

高显彩， 单雪红， 张丽慧

(1．宿州学院数学与统计学院，安徽 宿州234000;2．宿州市第二中学，安徽宿州234000)

0 引言

Gelenbe[1]在20世纪90年代首次提出了负顾客的排队模型．负顾客可以看成是某些工作的外来援助或取消信号，一般作为系统的制约因素而存在，能抵消系统中的正顾客．关于负顾客排队系统的研究近年来取得了较大的进展[2－6]，本文研究了带负顾客和Bernoulli反馈的M/G/1休假排队系统模型．日常生活中有许多相应的例子，如:在通讯系统中，数据传输到接受台，数据传输看成正顾客的到达，外来的干扰信号看成负顾客的到达，当到接受台发现数据传输错误时，数据会被要求反馈再次传输．

1 模型的数学描述

(1)正、负顾客各自以到达率为 λ+，λ－的Possion流独立到达，负顾客到达时，若系统处于忙期，则带走一名正在接受服务的正顾客;若系统处于闲期或假期，则负顾客自动消失．负顾客只起抵消正顾客的作用，并不接受服务．

(2)正顾客在接受服务的过程中若没有被抵消，则在服务完后以概率θ(0＜θ≤1)离开系统，以概率1－θ反馈到队尾等待下次服务．

(3)正顾客的服务时间有一般分布函数B(t)，有概率密度函数b(t)，风险率函数μ(t)

(4)休假策略是空竭服务单重休假(E，SV)，休假时间V为一般连续型随机变量，其分布函数为:V(t)=P(V≤t)概率密度函数v(t)，风险率函数r(t)

顾客的到达时间间隔、服务时间、休假时间相互独立且各自独立同分布．

0＜ρ=是系统存在稳态分布的充要条件．

令N(t)表示时刻t系统中的正顾客数．I(t)=0，1，2分别表示t系统处于闲期、忙期和假期．显然{I(t)，N(t)}不是马尔可夫过程．引入补充变量X(t)，Y(t)分别表示正顾客在时刻t接受服务的时间和服务台已休假的时间．这样，随机过程{I(t)，N(t)，X(t)，Y(t)}成向量马尔可夫过程．定义:

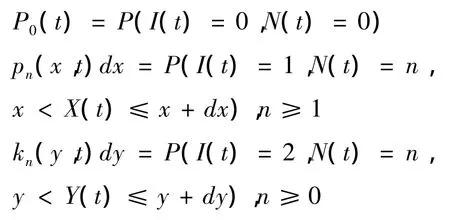
令

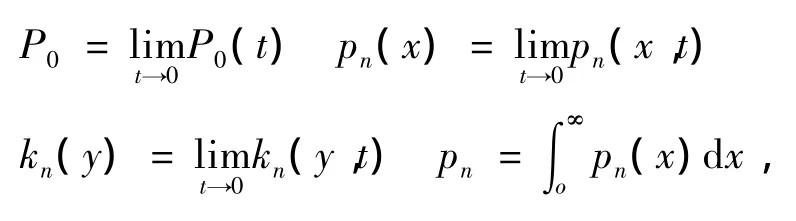
顾客的到达时间间隔、服务时间、休假时间相互独立且各自独立同分布．

0＜ρ=

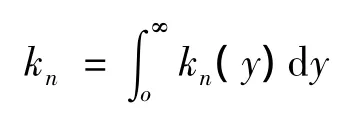
常用符号:Z变换:

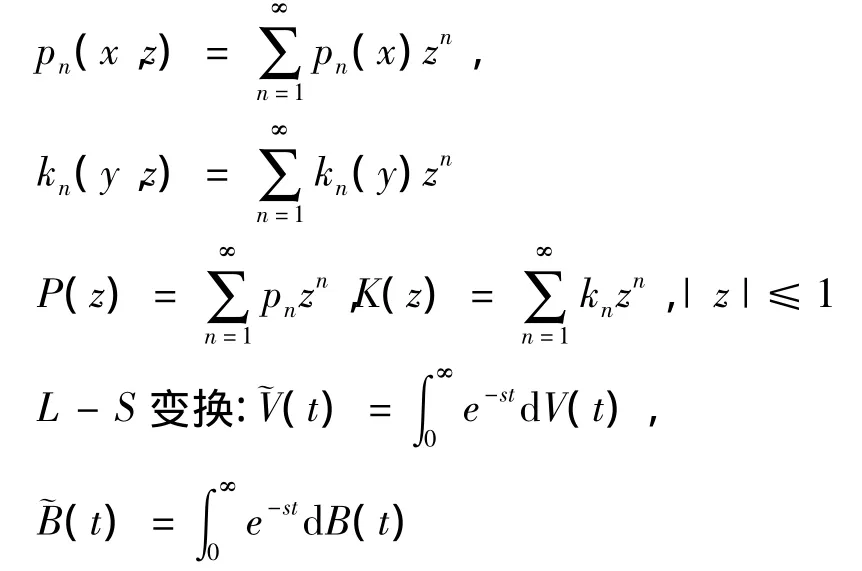
2 系统的状态方程组及求解

由状态转移和频度转移法则，分析可得稳态情况下系统的状态偏微分方程组:边界条件:

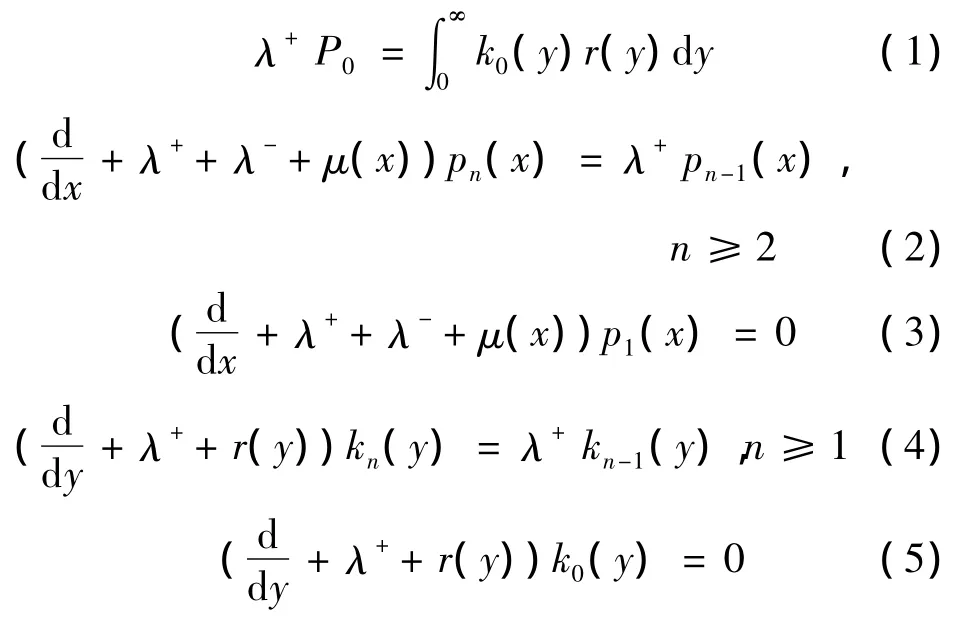
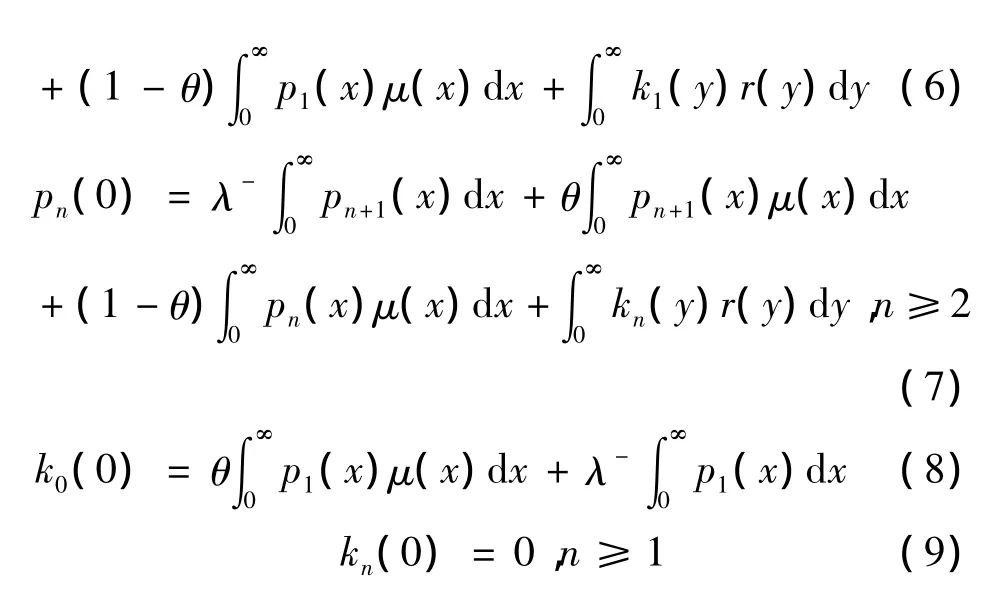
正则性条件:

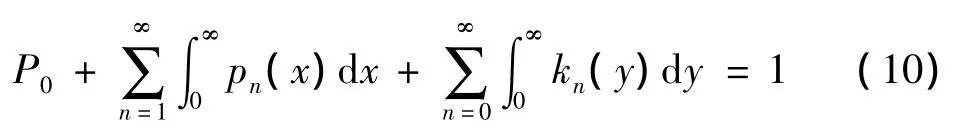
由(2)，(3)式可得:

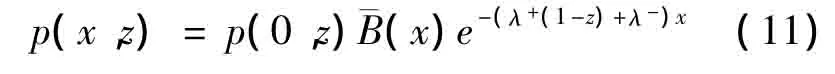
由(4)，(5)式可得:

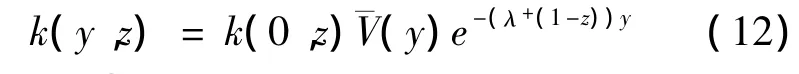
由(1)，(5)式可得:

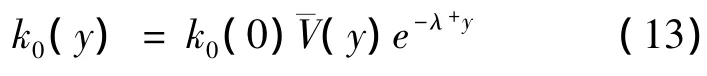
由(6)，(7)式可得:

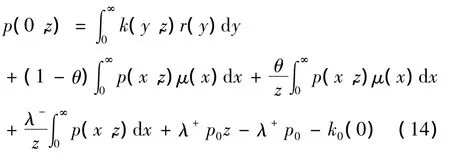
由(9)，(14)可得:

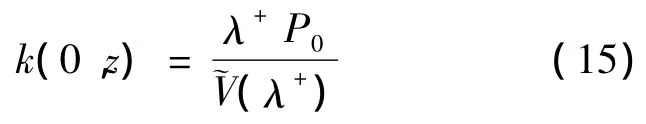
将(11)，(12)，(15)带入，(14)式整理可得:

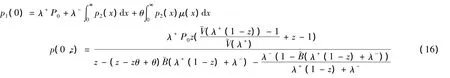
由(11)，(16)式可得:

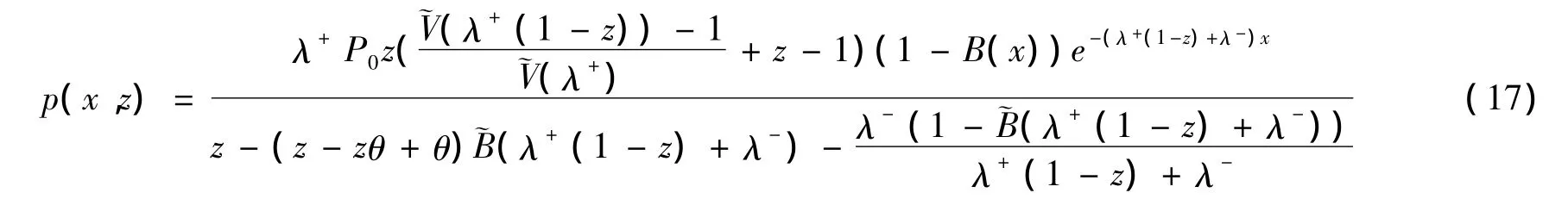
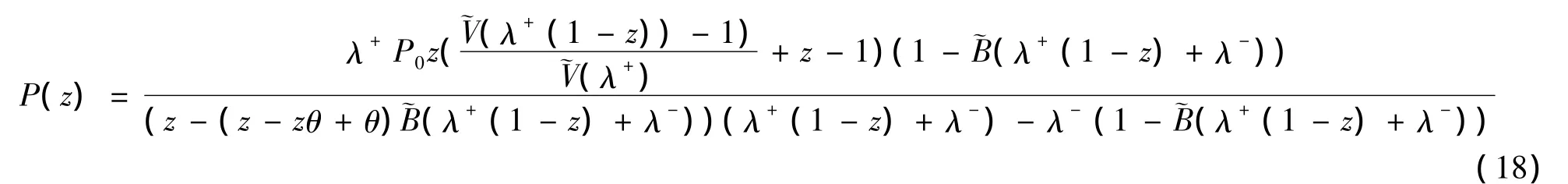
由(12)，(15)式可得:

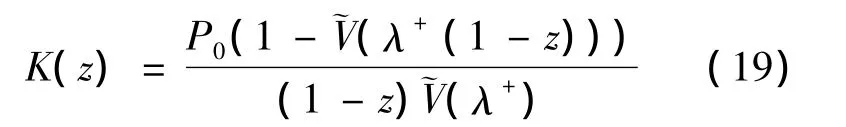
3 主要排队指标

定理1: 带负顾客和Bernoulli反馈的M/G/1

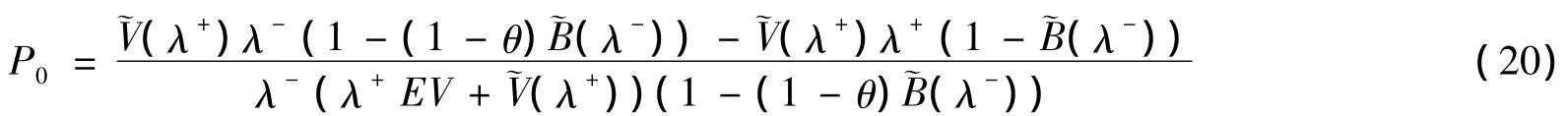
休假排队系统，系统处于闲期的概率是证明: 由(10)式可知:P0+P(1)+K(1)=1，当z=1时，(18)式右端是型的，且右端分式的分子、分母关于z的导数都存在，故由L'Hospital法则可得:P(1)

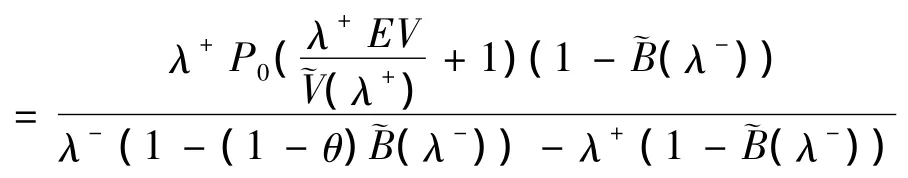
同理可得:K(1)

把P(1)，K(1)式代入P0+P(1)+K(1)=1即可求得(20)．

定理2: 带负顾客和Bernoulli反馈的M/G/1休假排队系统，系统处于休假期的概率是其中P0由(20)式给出．

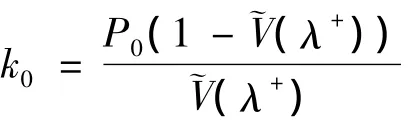
证明:

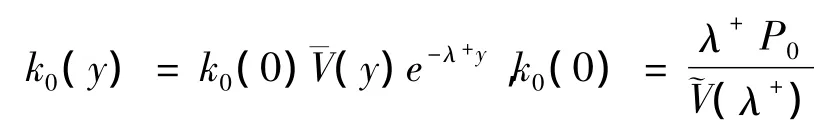
可得:

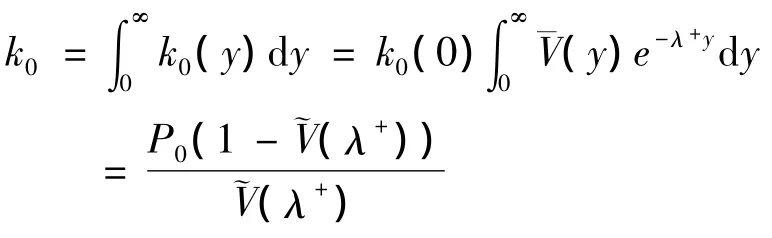
定理3: 带负顾客和Bernoulli反馈M/G/1的休假排队系统，系统稳态队长的概率母函数是

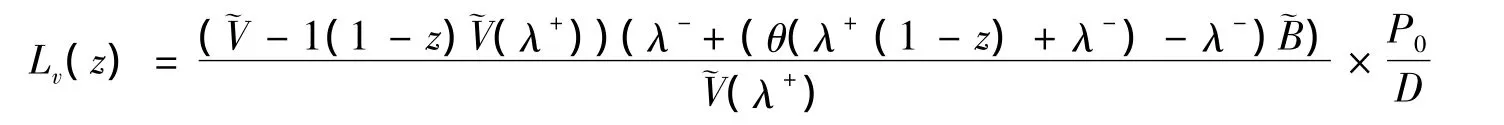
其中

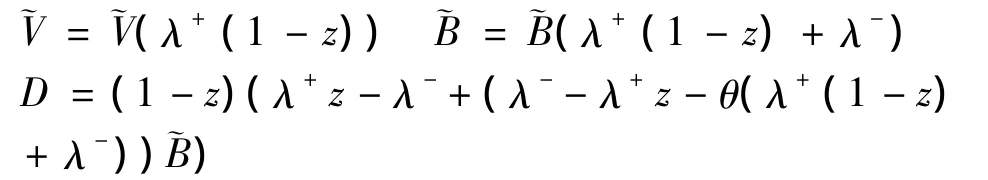
证明: 由Lv(z)=P0+P(z)+K(z)可得结论．

本文研究了带负顾客和 Bernoulli反馈的M/G/1休假排队系统，求得了系统处于闲期的概率和休假期间无正顾客的概率，得到了系统稳态队长的概率母函数，关于负顾客的排队模型有待于进一步研究．

[1] Glenbe E．Queues with Negative Arrivals[J]．Appl．Prob．1991，28:245－250．

[2] Harrison P G，Pitel E The M/G/1 Queue with Negative Customers[J]．Adv．Appl．Prob．1996，28:540 －566．

[3] Bayer N，Boxma O J．Wiener－ Hopf Analysis of an M/G/1 Queue with Negative Customers and of a Relative Class of Random Walks[J]．Queueing Systems．1996，23:301 －316．

[4] Zhu Y J．Analysis on a Type of M/G/1 Models with Negative Arrivals[R]．Proceeding of the 27th Stochastic Precess Conference University of Cambrige，UK，July 2001．

[5] 杜贞斌，朱翼隽等．负顾客的M/G/1排队模型[J]．江苏大学学报，2002，(3):91－94．

[6] 朱翼隽，陈燕．负顾客排队系统的研究进展[J]．江苏大学学2004 25(1):48－51．