随机利息力下的确定年金

安 勇

（山西大学商务学院，山西太原 030031）

0 引 言

年金是指按相等时间间隔形成的系列收支。分期付款赊购、分期偿还贷款、养老金给付、分期支付项目欠款等都属于年金收付形式。按照收付的次数和给付的时间划分，年金有标准年金、预付年金、延期年金、永续年金等几类。

对于年金定价问题的探讨，主要是在利率假设下确定它的各阶矩，尤其是一、二阶矩。为了便于讨论，传统的精算理论通常假定利率在整个研究期间内为常值。但实际经济生活中，作为资金价值的表现形式，影响利率的因素相当多，比如平均利润率、币资金的供求关系、物价上涨率、宏观政策、国际金融市场利率等，利率水平是各种因素综合作用的结果，鉴于此，利率往往具有不确定性。因此，在随机利率下对年金的时间价值进行探讨将更具有实际价值。近年来，学术界在假设利率为时间的连续函数以及离散函数两种情况下，对各种年金的定价问题进行了研究：

1）文献［1－4］假定利率是连续变化的，并分别采用维纳过程、维纳过程和O－U过程、反射布朗运动刻画利率期限结构，进而研究了各类年金或生存年金的定价问题，推导出了各阶矩的简洁形式；

2）文献［5－8］假设利率是时间的离散函数，在此基础上，给出了各类年金的一、二阶矩的表达式。上述文献的共同点都是假设各年利率之间是相互独立的。但实际上，作为时间序列数据，前期的利率对后期利率的变化将产生一定的影响，而且时间间隔越小，影响越大。因此，在假设各年利率相关的条件下对年金或生存年金的定价问题进行研究更符合实际情况。

文中假设当期利率只与过去两期的利率有关，进而利用MA（2）模型对利息力进行建模。然后，在利息力基本假设条件下，探讨了期末付虹式年金的定价问题，给出了此种年金现值的一、二阶矩的简洁计算公式。随后，通过数值例子研究了相关参数对一阶矩的影响，其结论对年金定价及其敏感性分析具有一定的参考价值。

1 固定利率下标准年金的现值

假设固定利率为j（j≠－1），利息力为δ，则折现因子，在n年内每年年末支付额为1的期末付年金的现值为

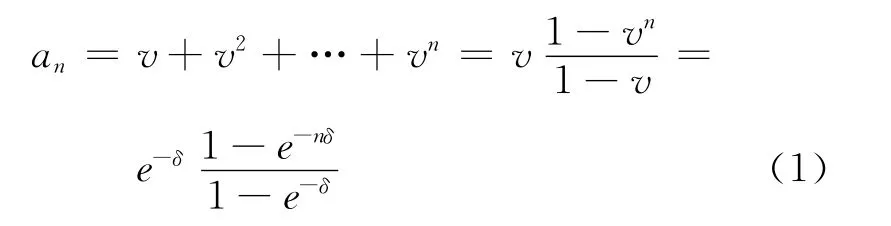
n年内每年年初支付额为1的期初付年金的现值为：

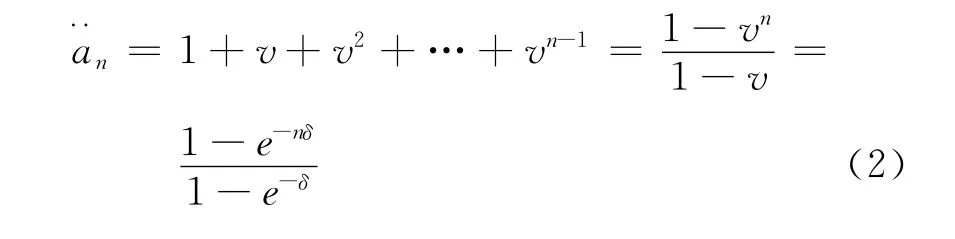
2 随机利息力下期末付虹式年金现值的一、二阶矩

2.1 利息力基本假设

假设当期利率只与过去两期的利率有关，进而利用MA（2）模型对利率期限结构进行描述：

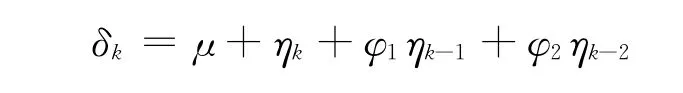
式中：δk——第k期的利息力；

并且假设M（t）＝E（etη）为变量η的矩母函数。

为了便于研究，我们给出一些记号：

2.2 支付额逐年递增的年金现值的期望

用（Ia）n表示n年内每年年末分别支付1，2，…，n的递增形式年金的现值，即

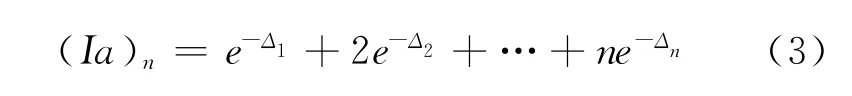
定理1 在利息力基本假设下，有

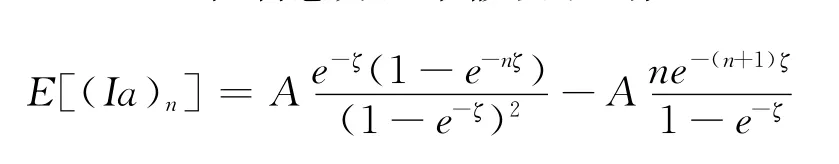
证明：

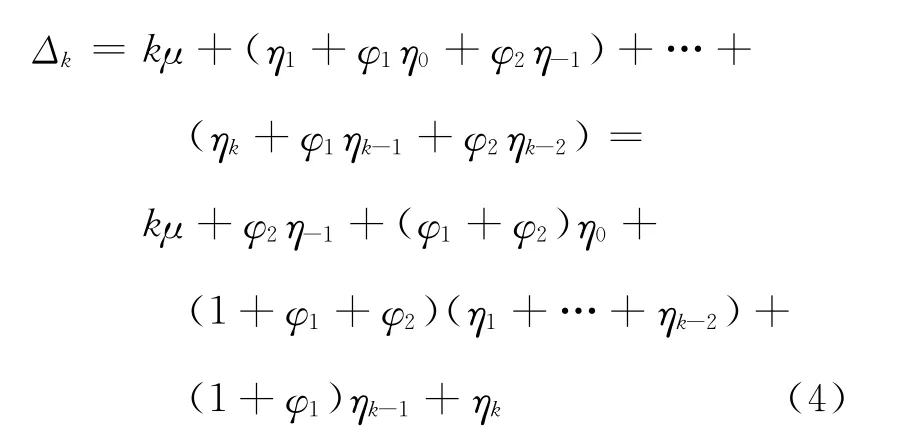
由第k年的折现因子

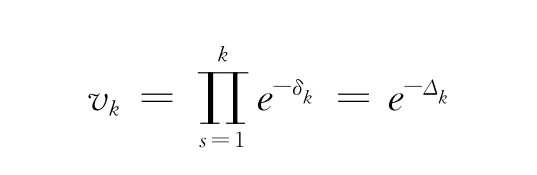
得

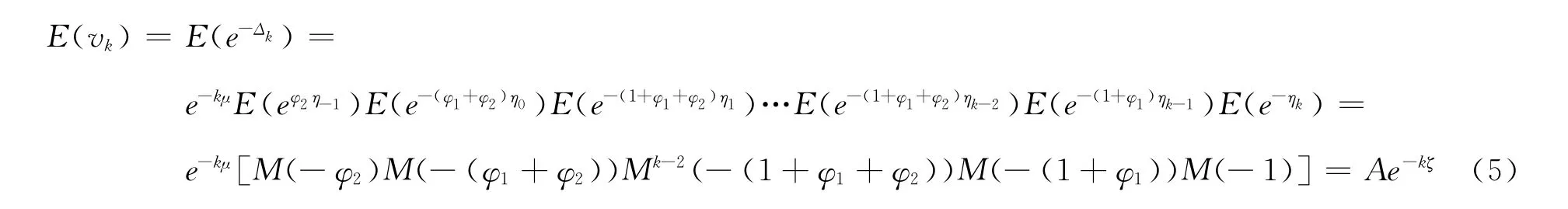
因此

式（6）乘以e－ζ，得

式（7）－式（6）并整理，得

2.3 延期n年，支付额逐年递减的年金现值的期望

用n｜（Da）n－1表示延期n年支付，第n＋1年末支付额为n－1，而后逐年递减，至2n－1年末时，支付额为1的年金现值，即

定理2 在利息力基本假设下，有

2.4 期末付虹式年金现值的期望与方差

用（PV）2n－1表示每年年末分别支付1，2，…，n－1，n，n－1，n－2，…，2，1，共2n－1个付款期的年金现值，此年金称为期末付虹式年金，则

定理3 设（PV）2n－1为期末付虹式年金的现值，在利息力基本假设下，有

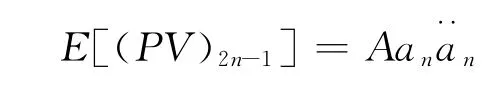
并且

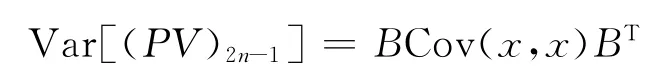
其中B＝（1，2，…，n，n－1，n－2，…，2，1）表示2n－1维行向量，x＝（e－Δ1，e－Δ2，…，e－Δ2n－1）T表示2n－1维列向量

为协方差矩阵，满足

且

证明：先证

由定理1和定理2可知

因此

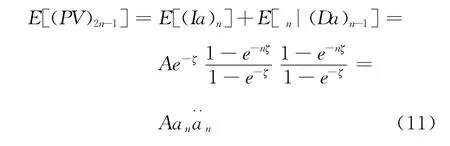
下证

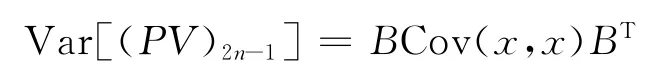
当r＜k时

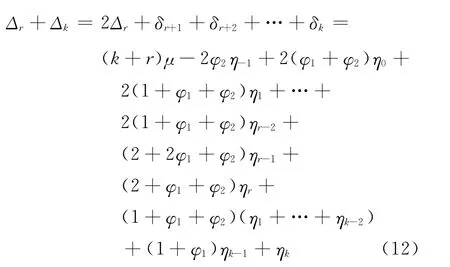
记

则

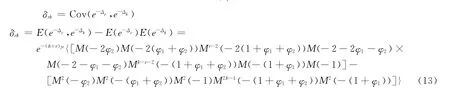
同理可得

由此

3 数值模拟

某分期付款采取期末付虹式年金的形式，假设随机干扰项服从标准正态分布ηk∈N（0，σ2），则ηk的矩母函数为M（t）＝e0．5σ2t2，在利息力基本假设下，由定理3可知，期末付虹式年金现值的期望值为

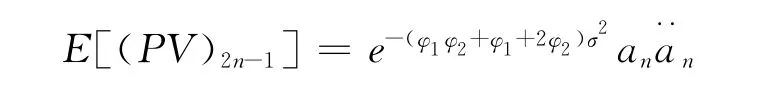
其中，ζ＝μ－0．5（1＋φ1＋φ2）2σ2为年金an，中相应的利息力。

不失一般性，基础数据假设为：常数利息力μ＝0．06，φ1＝0．5，φ2＝0．2，n＝30a，随机干扰项的方差为σ2＝0．072。

由基础数据可得，E［（PV）2n－1］＝224．853 1，而在常数利息力μ＝0．06的条件下，期末付虹式年金的现值为（PV）2n－1＝193．476 9。因此，为消除利息力不确定性带来的风险，各期付款的现值之和应增加16．2%。固定μ＝0．06，期限为n＝30a，σ2＝0．072。

不同的｛φ1，φ2｝组合对期末付虹式年金现值的期望值的影响如图1所示。

由图1可知，若未来利率受经济因素和投资结构影响，导致波动幅度增大，即｜φ1｜，｜φ2｜逐步增大时，期末付虹式年金现值的期望值将逐步增大，而且变化速率随｜φ1｜，｜φ2｜的增大而逐步加快。此结论从侧面说明，利率频繁波动将对经济，尤其是金融活动产生巨大的影响。因此，追求利率稳定是非常有必要的。

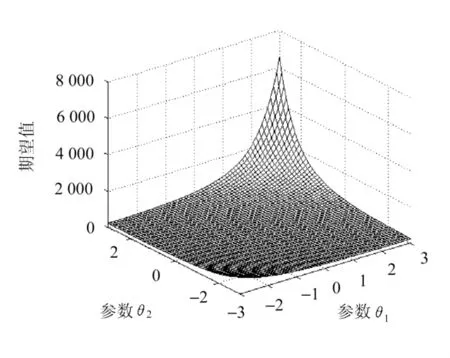
图1 相关参数对期末付虹式年金现值的期望值的影响

［1］ Beckman，Fuelling C P．Extra randomness in certain annuity models［J］．Insurance：Mathematics and Economics，1991，10（2）：275－287．

［2］ 谢小良．未来现金流的矩研究［J］．系统工程，2004，22（4）：36－38．

［3］ David Perry，Wolfgang Stadje．Function space integration for annuities［J］．Insurance：Mathematics and Economics，2001，29（1）：73－82．

［4］ 郭春增，王秀瑜．随机利率下的寿险精算模型［J］．统计与决策，2008，9（2）：53－55．

［5］ Zaks A．Annuities under random rates of interest［J］．Insurance：Mathematics and Economics，2001，28（1）：1－11．

［6］ 王丽燕，杨德礼．一类随机利率下的确定年金［J］．数学的实践与认识，2005，35（12）：7－12．

［7］ 刘凌晨．随机贴现率下的年金分析［J］．长春工业大学学报：自然科学版，2010，31（2）：231－234．

［8］ 潘红宇．金融时间序列模型［M］．北京：对外经济贸易大学出版社，2008．