基于GM（1，1）的可变季节指数预测模型

何 俊， 刘会茹， 张彦群

（1．郑州升达经贸管理学院，河南郑州 451191；2．石家庄经济学院，河北石家庄 050073；3．郑州市环境监测中心站，河南郑州 450002）

0 引 言

GM（1，1）预测模型将一切随机变量看作是在一定范围内变化的、仅与时间有关的灰色过程［1］。它的基本方法就是用指数曲线拟合原始点列，由此对原始点列进行预测。与其它预测方法相比，具有原始数据少、计算简单、预测精度高等特点［2］。但GM（1，1）模型在拟合含有季节变动因素的时间序列时效果较差。在现实生活中，季节变动是一种极为普遍的现象，季节指数预测法能反映出这种季节变动的情况［3－4］。文献［5－7］采用GM（1，1）模型拟合原始数据，确定趋势值，然后用各期平均季节指数修正趋势值。这种方法虽然能反映季节变动的因素，但是忽视了季节因素随时间推移而变化的趋势。而季节变动预测法中的可变季节指数预测法适用于某变量具有线性增加或减少的趋势，同时受季节因素的影响，这种季节因素随着时间的推移有逐渐加大（或减少）的趋势［8］。文中在分析2006－2010年郑州市氮氧化物的日均浓度后，发现其构成的时间序列具有季节特征，由此建立了基于GM（1，1）的可变季节指数预测模型，为政府部门制定环境质量监控计划和决策管理提供了依据。

1 建立GM（1，1）模型

GM（1，1）模型由一个单变量的一阶微分方程构成。设原始数据列

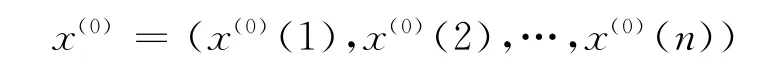
作一次累加生成序列

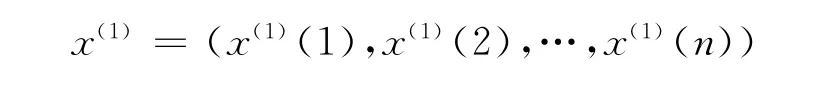
其中

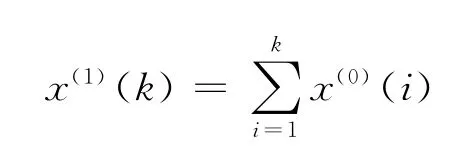
k＝1，2，…，n

对x（1）建立GM（1，1）模型，对应的微分方程为：

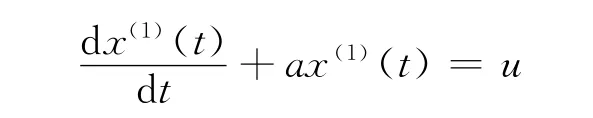
记参数列为α，α＝（a，u）T，令

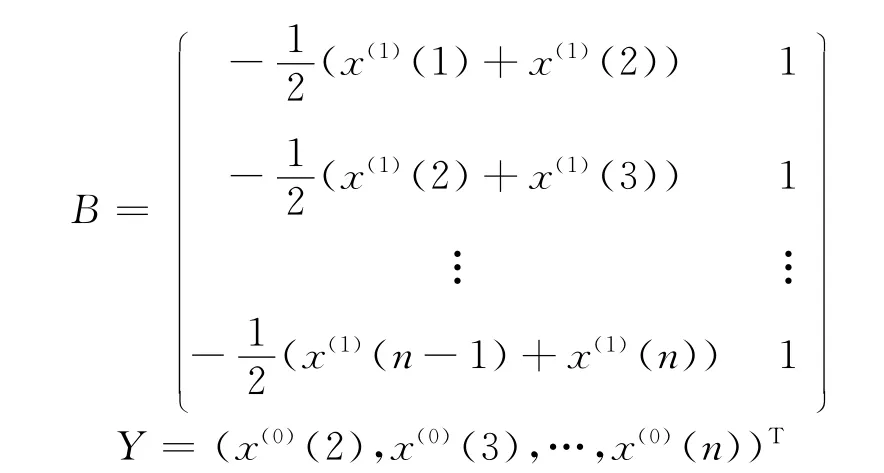
由最小二乘法得

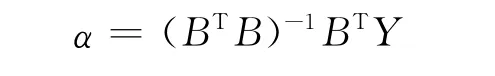
因此，GM（1，1）模型的离散解形式为：对模型进行累减运算得到原始序列的预测值

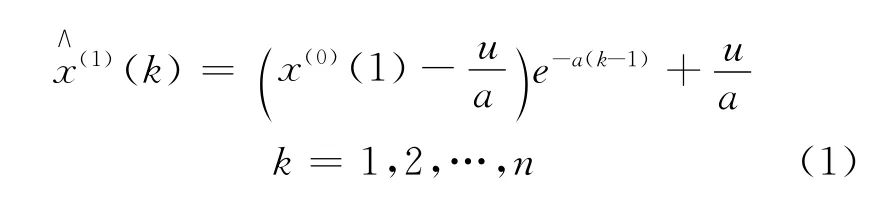
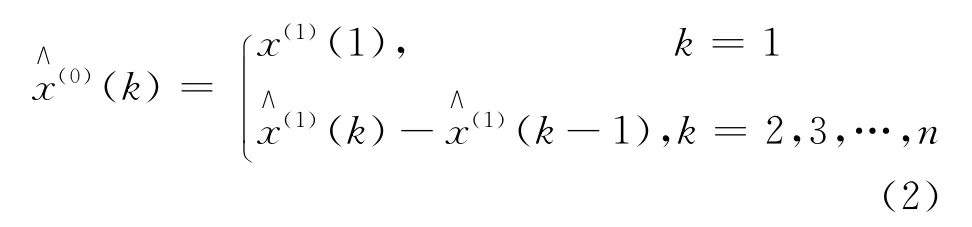
2 建立基于GM（1，1）的可变季节指数预测模型

2）将实际观测值x（0）（k）除以GM（1，1）预测的趋势值（k），得出趋势季节比率：

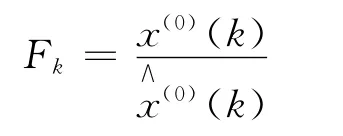
k＝1，2，…，n 3）采用直线拟合各期同季趋势季节比率：

式中：i——一个周期内第i季；

m——周期数；

ai，bi——待定参数。

4）由最小二乘法确定ai，bi

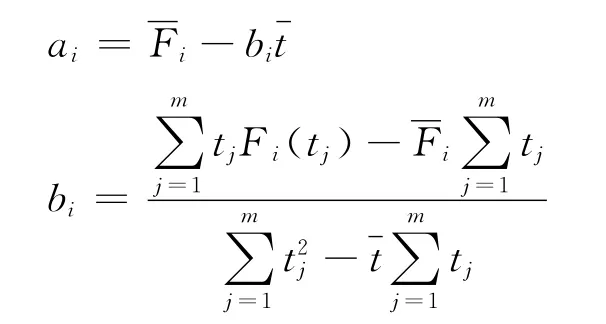
其中

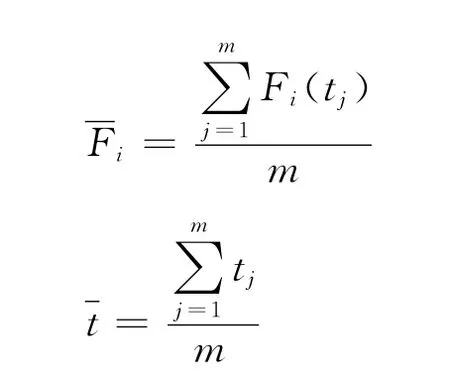
5）建立基于GM（1，1）的可变季节指数预测模型

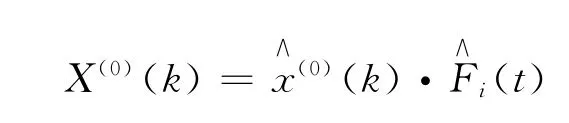
3 基于GM（1，1）的可变季节指数预测模型在郑州市空气污染物浓度预测中的应用

根据郑州市2006－2010年春、夏、秋、冬四季环境空气污染物氮氧化物的日均浓度值资料建立预测模型，并预测2011年四季氮氧化物的日均浓度。

3.1 建立郑州市四季环境空气污染物氮氧化物的日均浓度值的GM（1，1）模型

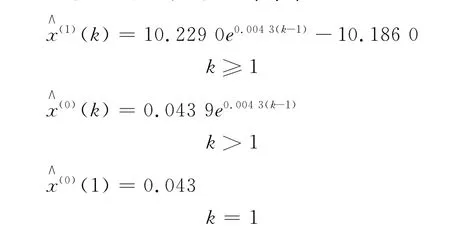
由GM（1，1）模型预测的趋势值见表1。

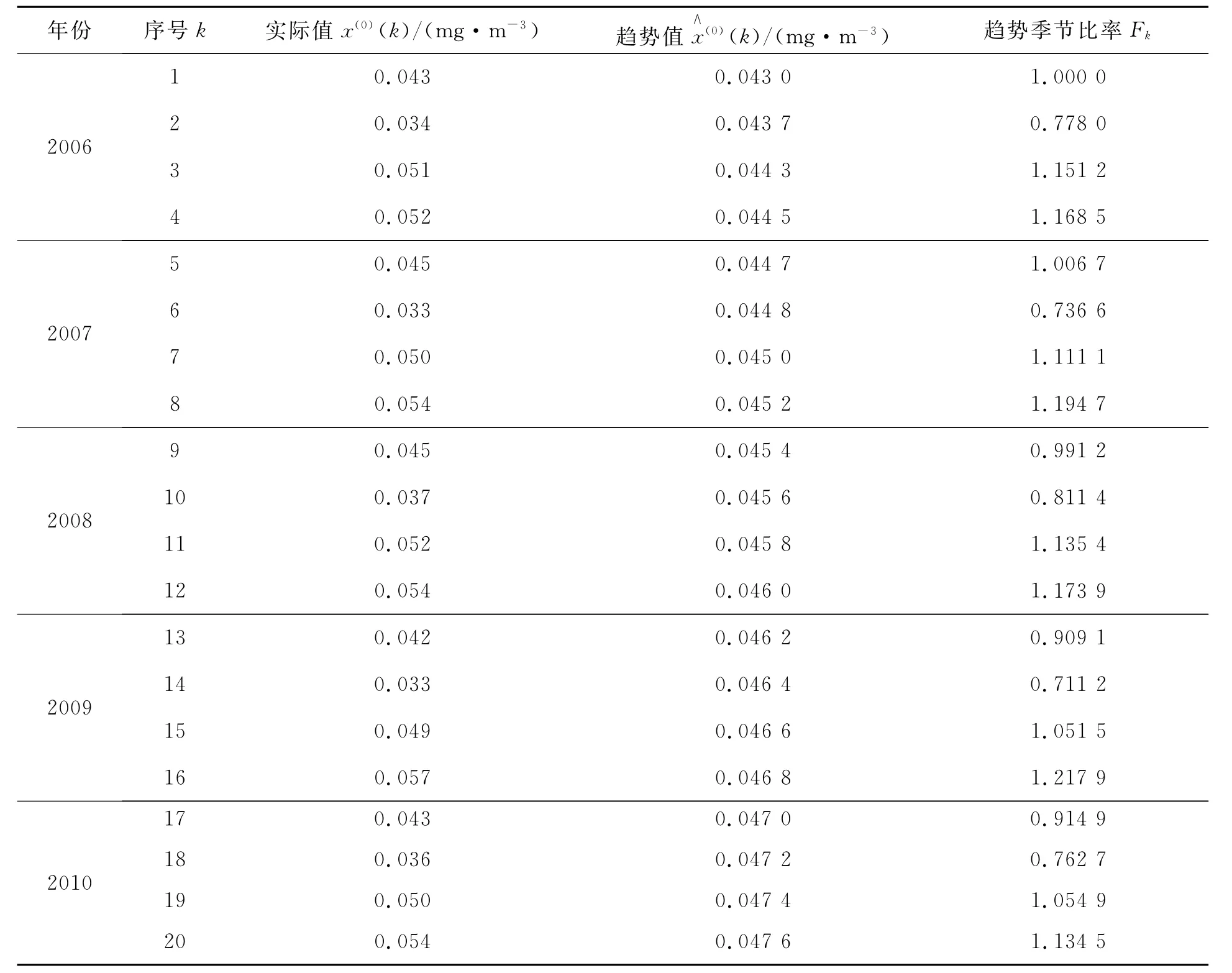
表1 郑州市2006－2010年四季氮氧化物的日均浓度值和趋势值

3.2 采用直线拟合各期同季趋势季节比率

计算各期同季的季节指数拟合值见表2。

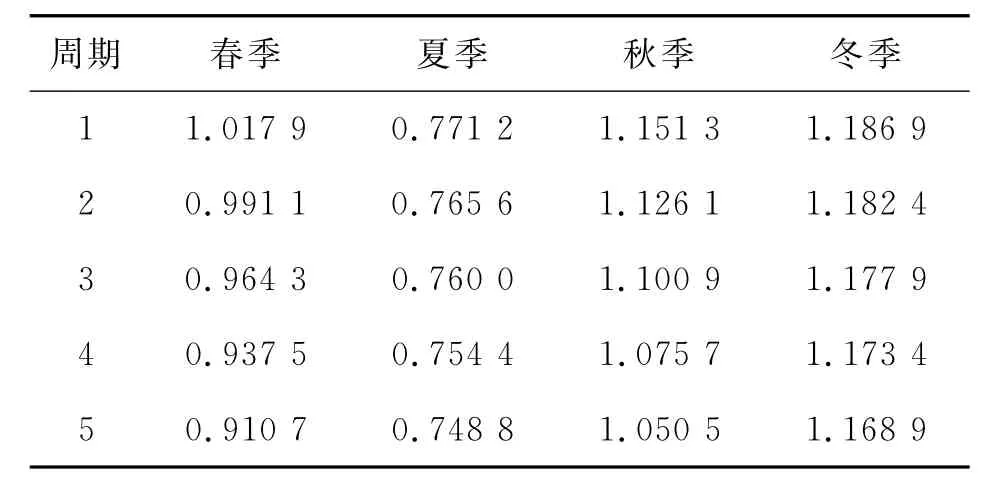
表2 各期同季的季节指数拟合值

3.3 建立基于GM（1，1）的可变季节指数预测模型及检验误差

模型为：

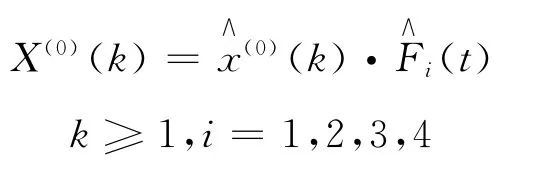
模型的模拟效果可以通过相对误差来检验，见表3。

拟合效果如图1所示。

从表3和图1可以看出，GM（1，1）模型在拟合含有季节变动因素的时间序列时，效果较差，平均相对误差高达15．027 2%；但基于GM（1，1）的可变季节指数预测模型，平均相对误差只有2．273 7%，使预测精度大幅度提高。

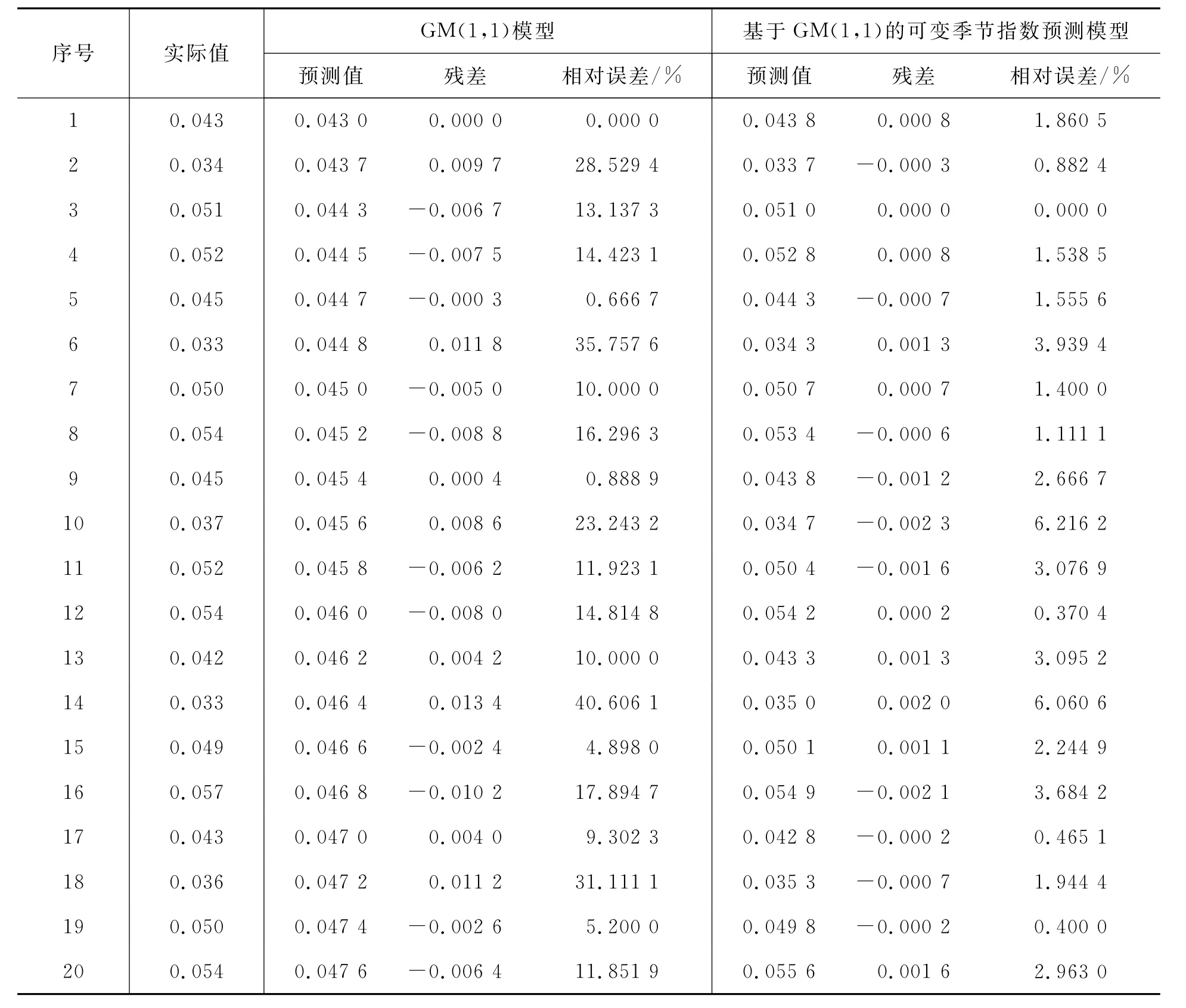
表3 模型误差检验表

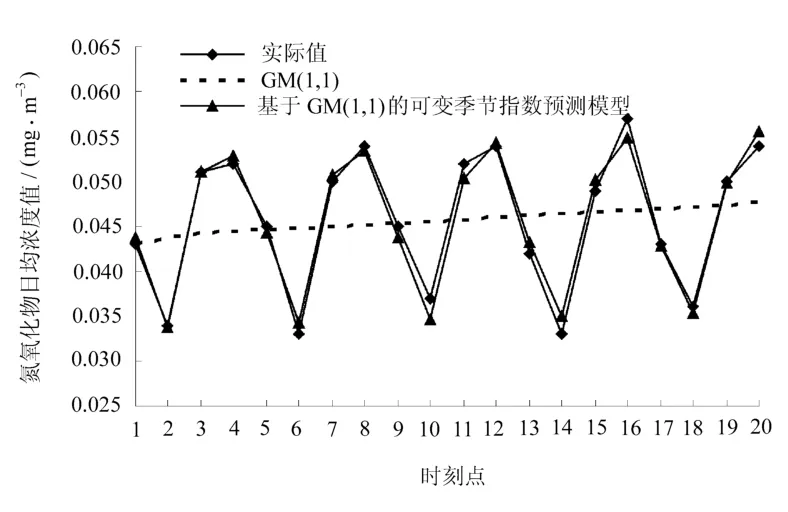
图1 模型拟合效果图

3.4 用基于GM（1，1）的可变季节指数预测模型预测2011年郑州市春、夏、秋、冬四季环境空气污染物氮氧化物的日均浓度

当k＝21时：

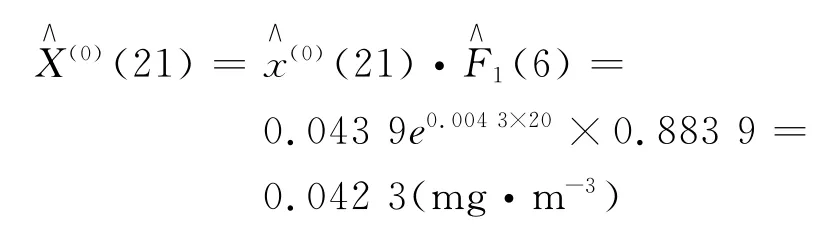
当k＝22时：

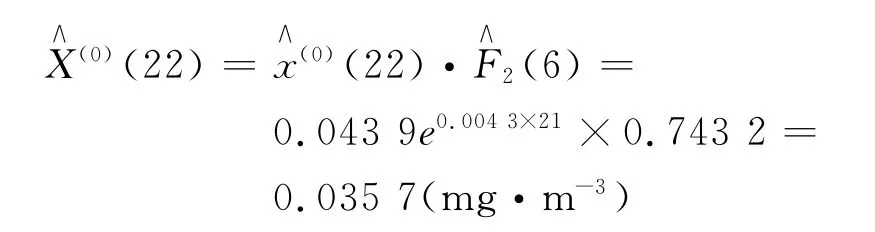
当k＝23时：

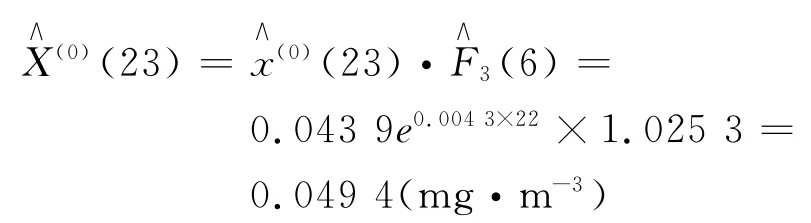
当k＝24时：

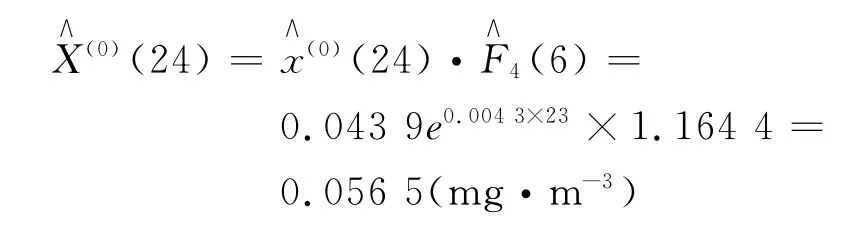
由计算结果可知，2011年郑州市春、夏、秋冬四季空气污染物氮氧化物的日均浓度预计为0．042 3，0．037 5，0．049 4，0．056 5mg·m－3。

4 结 语

基于GM（1，1）的可变季节指数预测模型是以GM（1，1）为基础，即用GM（1，1）模型对时间序列中的趋势值进行拟合，然后用可变季节指数修正。因此，与GM（1，1）模型相比，既可以反映时间序列的趋势变化，又可以反映季节因素随时间的变化趋势，从而在对含有季节变动因素的时间序列预测中，精度大幅度提高。

［1］ 邓聚龙．灰预测与灰决策［M］：武汉：华中科技大学出版社，2009：99－105．

［2］ 刘思峰，党耀国．灰色系统理论及其应用［M］．北京：科学出版社，2005．

［3］ 刘莉．基于灰色预测模型与季节指数的区域物流需求预测［J］．物流技术，2010（4）：41－43．

［4］ 纪跃芝，范小娜．利用指数平滑法预测经济变量［J］．长春工业大学学报：自然科学版，2003，24（1）：61－62．

［5］ 曹小艳．GM（1，1）季节因素修正模型在预测中的应用［J］．问题研究，2002（3）：12－14．

［6］ 杨俊祥，程盛芳．灰色－周期外延组合模型在煤炭需求预测中的应用［J］．统计与决策，2010（13）：162－163．

［7］ 朱星辉，朱金福．季节性组合预测模型在航空旅客需求中的应用研究［J］．统计与决策，2007（1）：49－50．

［8］ 郝全明．灰色理论及季节变动指数在原煤生产量预测中的应用研究［J］．内蒙古科技大学学报，2007（4）：293－296．