基于分位算法的汽车变速器故障诊断
2012-07-09潘晖,刘泽
潘 晖, 刘 泽
(长春工业大学基础科学学院,吉林长春 130012)
0 引 言
近年来,在汽车变速器的故障诊断方法研究中,“极限参数法”理论[1-2]得到了广泛应用。由德国迪斯卡姆公司与美国戴姆勒-克莱斯勒公司合作开发的ROTAS-GP振动噪声检测系统[2]就是以“极限参数法”理论为基础,建立了基于标准差算法的故障诊断模型。该模型要求训练样本数据必须具有一定规模且满足正态分布,因此,这种约束条件仅适用于大子样水平的样本。但是汽车变速器在生产实践中,受生产条件和成本的限制,一般很难在初始阶段提供大量样本进行系统的学习和训练,只能通过不满足正态分布的小子样水平的样本进行基本训练,使系统具备初步的判别能力,所以,该模型在汽车变速器生产实践初期会存在很大的误差,导致错误的学习结论。
文中基于分位算法提出了一种汽车变速器的故障诊断方法。由于分位数在计算过程中不受样本规模、样本数据统计分布与极端异常值的影响,使得该方法能够在汽车变速器整个生产实践过程中,对存在故障的汽车变速器作出迅速、准确的故障判别。
1 极限参数
由于汽车变速器的振动信号[3]成分比较复杂,为了防止对故障作出漏判或误判的情况,应对振动信号进行时域和频域的综合分析[4]。
1.1 时域极限参数
汽车变速器存在故障的一个重要表现形式是产生较大的噪声。噪声的幅度决定于产生非正常振动的能量,由此在检测过程中,可以通过分析时域信号中反映振动加速度幅值变化的峰值、平均值和极差值,刻画噪声能量的变化规律,达到分析噪声幅度的目的。对于一给定的振动信号,其样本数据观测矩阵X为

式中:n——观测样本个数;
m——每个观测样本的大小。
其中,由m个数据组成的第i个观测样本向量可记为

i=1,2,…,n令j表示某一观测样本中数据的序号,则有:

i=1,2,…,n,j=1,2,…,m
式中:Peak——峰值,反映了每个观测样本的最大振幅;
RMS——平均值,反映了每个观测样本的平均幅度,即每个观测样本所包含的能量;
Crest——极差值,反映了峰值Peak与平均值RMS的差值。
Peak,RMS和Crest计算原理如图1所示。
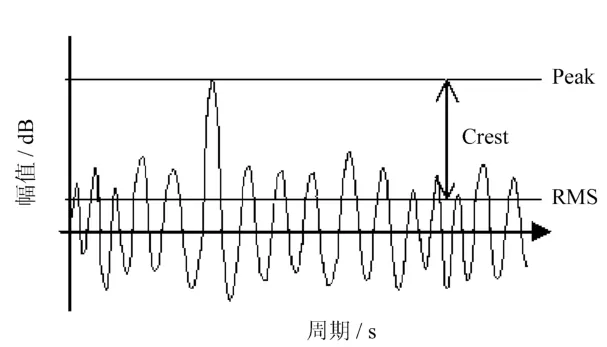
图1 Peak,RMS和Crest计算原理示意图
1.2 频域极限参数
对时域信号使用快速傅里叶变换[5](FFT)的方法进行时频变换[6-7],将时域信号转换为阶次谱,所提供的频域特征可以作为故障分类的特征。
对1.1中样本数据观测矩阵X进行时频变换,得到阶次谱集合
Sn={S1,S2,…,SN}
式中:n——观测样本个数;
N——阶次数。
Sn的幅值矩阵为:

则第l阶的幅值向量为
Sl=(a1l,a2l,…,anl)T
l=1,2,…,N
一组时域信号经过时频变换后得到的阶次谱如图2所示。

图2 经FFT变换后得到的阶次谱
2 汽车变速器故障诊断方法
2.1 基于标准差故障诊断模型[2]
标准差也称均方差,是用于衡量一组数据中某一数值与其平均值差异程度的指标,能综合反映一组数据的离散程度或个别差异程度。
由1.1中的观测样本向量Xi,可得其标准差(Xi)std为

i=1,2,…,n
j=1,2,…,m
基于标准差算法的时域极限参数故障诊断模型为:

式中:Peakth,RMSth,Crestth——分别表示Peak,RMS和Crest的极限值;
Peakstd,RMSstd,Creststd——分别表示Peak,RMS和Crest的标准差;
3Peakstd,3RMSstd,3Creststd——分别表示Peak,RMS和Crest的标准差的置信区间[8]。
基于标准差算法的频域极限参数故障诊断模型为
(Sn)th={(S1)th,(S2)th,…,(Sl)th,…,(SN)th}其中
(Sl)th=+3(Sl)std
l=1,2,…,
N式中:(Sl)th——第l阶幅值向量的极限值;
(Sl)std——第k阶幅值向量的标准差;
3(Sl)std——第k阶幅值向量的标准差的置信区间。
由统计理论假设检验理论可知,RMS,Peak和Crest以及各阶次的极限值的置信度为99%,即99%的训练样本取值均将不超出此范围。
2.2 基于分位算法故障诊断模型
分位数[8]是用于反映顺序数据的集中趋势的一种统计测度值,提供了有关各数据项如何在最小值与最大值之间分布的信息。
设1.1中的观测矩阵X的分布函数为
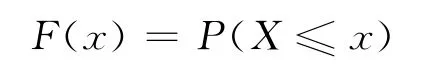
对给定的p∈(0,1),方程F(x)=p的解

称为该总体(或该分布)的p分位数。
在建立基于分位算法的故障诊断模型时,引入了修正参数。在观测样本逐渐积累的过程中,通过调整参数值,对诊断模型中的极限值进行修正,形成新的、具有更强鲁棒性的极限参数,使诊断模型得到更高的泛化精度。
基于分位算法的时域极限参数故障诊断模型为:

式中:Peakth,RMSth,Crestth——分别表示Peak,RMS和Crest的p分位数;
kPeak,kRMS,kCrest——分别表示Peak,RMS和Crest的修正系数。
基于分位算法的频域极限参数故障诊断模型为:
(Sn)th={(S1)th,(S2)th,…,(Sl)th,…,(SN)th其中
(Sl)th=(Sl)p×kl
l=1,2,…,N
式中:Sl)th——第l阶幅值向量的极限值;
(Sl)p——第l阶幅值向量的p分位数;
kl——第l阶的修正系数。
3 实例结果
本实验使用的数据为试验现场采集的汽车变速器振动信号。将整个观测样本集分为两部分,即训练样本集和测试样本集。在训练样本集中提取样本,形成小子样水平、中子样水平和大子样水平的3个训练样本集,分别对这3个样本集进行学习训练,提取时域极限参数和频域极限参数,分别建立基于标准差算法和基于分位算法的故障诊断模型,并用两种模型依次对测试样本进行故障判别,对测试结果进行对比。
为了介绍方便,将基于标准差算法的故障诊断模型称为模型1,将基于分位算法的故障诊断模型称为模型2。时域极限值对比结果见表1。
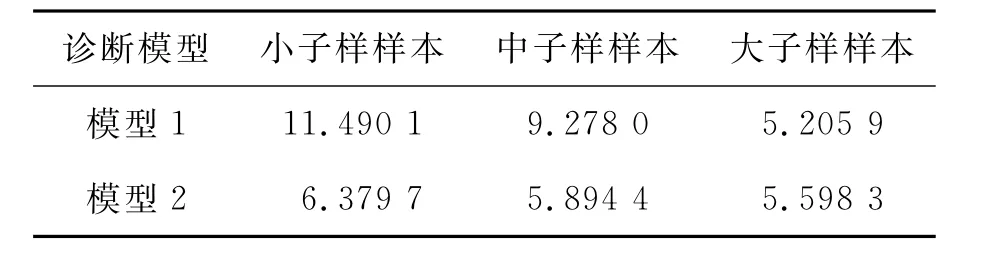
表1 时域极限值对比
从表1中可以看出,对于3个样本集,使用模型1得到的极限值大于使用模型2得到的极限值。
在频域极限参数值的分析中,将所有阶次的极限值连接起来,形成一条曲线,称为极限曲线。对比结果如图3~图5所示。
从频域分析的角度看,图3~图5分别表示小子样样本、中子样样本和大子样样本的极限曲线对比情况。
从图中可以更为直观地看出模型1与模型2的差别。对于3个样本集,使用模型1得到的极限曲线明显大于使用模型2得到的极限曲线。

图3 小子样样本极限曲线对比图
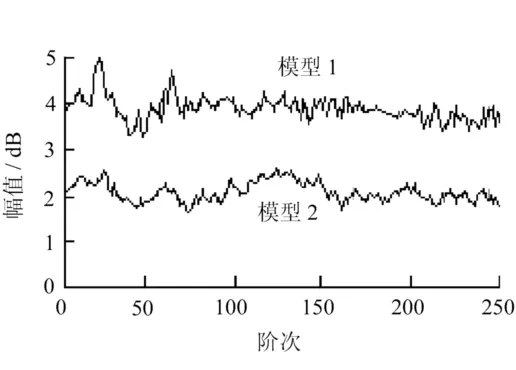
图4 中子样样本极限曲线对比图

图5 大子样样本极限曲线对比图
通过时域和频域两种分析方法,对模型1和模型2进行综合对比,结果见表2。

表2 两种模型的综合对比
从表2中可以看出,模型1与模型2在实验中所用的时间都很短,而且相等,这对汽车变速器的在线快速检测十分重要;在学习初期,训练样本库中仅有少量训练样本时,使用模型2进行故障判别的误判率要远远小于使用模型1的误判率;随着样本数量的不断积累,两种诊断模型的误判率都有很大程度的下降,但是模型2的误判率仍然小于模型1的误判率;当训练样本数足够大时,即满足正态分布时,两种诊断模型基本达到相同的判别精度。
4 结 语
实验结果表明,基于分位算法的故障诊断模型与基于标准差算法的故障诊断模型相比,在仅有少量训练样本的学习初期,得到的极限参数值更为准确。在后期生产过程中,大量的样例数据逐渐积累,通过调整修正参数值,使故障诊断模型具有更强的自适应能力和更高的泛化能力,提高了对汽车变速器故障诊断的精度,这在实际应用中具有非常重要的意义。
[1] 尚文利,史海波,何柏涛.设备维护模式选择决策支持框架研究[J].机械设计与制造,2006,12:127-128.
[2] DISCOM GmbH.Gearbox analysis system ROTAS-GP[EB/OL].[2006-08-15](2011-09-18).http://www.discom.de.
[3] 于柏森.基于神经网络的发动机故障诊断分类器设计[D]:[硕士学位论文].长春:长春工业大学,2010.
[4] 魏宏亮.汽车发动机机械故障诊断系统装置与特征抽取算法研究[D]:[硕士学位论文].长春:长春工业大学,2007.
[5] 姜建国,曹建中,高玉明.信号与系统分析基础[M].北京:清华大学出版社,1997.
[6] 张贤达.非平稳信号分析与处理[M].北京:国防工业出版社,1998.
[7] 王志杰.齿轮箱振动信号时频分析与故障诊断[D]:[硕士学位论文].重庆:重庆大学,1999.
[8] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006.
