基于KIVA的发动机进气道稳流模拟计算
2012-07-09魏明锐周昌祁王海良
魏明锐 周昌祁 文 华 李 程 王海良
(武汉理工大学汽车工程学院1) 武汉 430070) (现代汽车零部件技术湖北省重点实验室2) 武汉 430070)(南昌大学机电工程学院2) 南昌 330031)
0 引 言
进气道的设计是发动机开发过程中的重点与难点.进气道的传统设计方法是采用经验设计和稳流试验相结合,利用木模或石膏模在稳流试验台上不断试验和优化,确定气道的形状,根据气道形状设计二维图纸,最终制造模具,用于生产.这一开发过程最大的弊端就是必须要有一个原型样件作参考,这将大大制约缸盖设计工程师对发动机的全新设计.理想的气道开发流程应为:三维造型→优化改进→抽气试验→快速成型,气道的三维造型设计模拟没有过多束缚,可根据相关的边界条件自由设计.设计更改时只要根据实验数据,对不满足产品要求的数据进行调整,直至最终确定符合性能的最佳气道形状[1],设计和制造周期大大缩短.
本文使用KIVA作为仿真工具,它具有2个主要特点:(1)KIVA程序采用非正交结构化网格,可以是任意六面体.计算网格分为结构化网格和非结构化网格,结构化网格的生成相对麻烦,但容易对控制方程进行离散,且求解精度比非结构化网格要高;(2)其源程序是开放的.研究者可在其原有模型的基础上使其更完善或更适用于某一特定的情况.
1 数学模型
1.1 气流运动的控制方程
KIVA软件通过对质量、动量、能量守恒方程和RNG-κ-ε湍流模型等偏微分方程在时间和空间上进行离散,求得具有物理意义的数值解,从而获得对流场细节的描述.考虑到活塞为运动边界,故采用任意拉格朗日-欧拉法(ALE)进行变网格流体计算.ALE在时间上采用一阶向前差分和空间上采用有限体积方法来离散控制方程组[2-3].
质量方程为
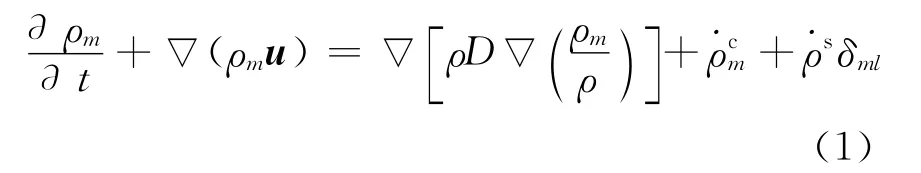
式中:ρm为第m种组分的密度;ρ为总密度;D为扩散系数;上标c为化学反应的源项;上标s为喷雾源项,下同;δml为Kronecker算子.
动量守恒方程为
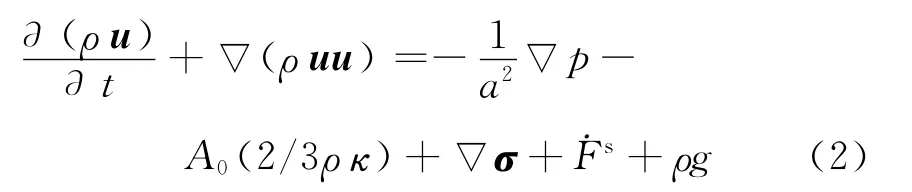
式中:a为PGS(pressure gradient scaling)系数,用于在低马赫数情况下增加计算的收敛速度;κ为湍流动能;σ为湍流粘性应力张量;常数A0=
能量守恒方程为
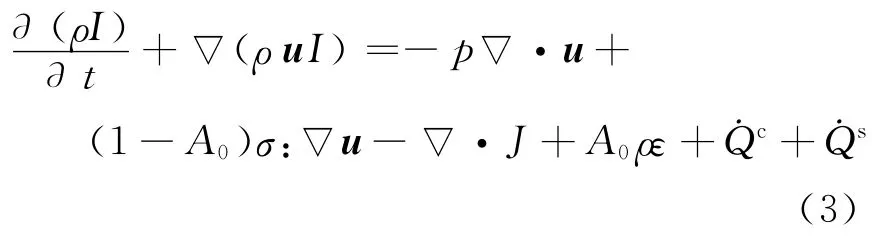
式中:J为热流量和分别为化学反应放热源项和喷雾放热源项.
κ方程为
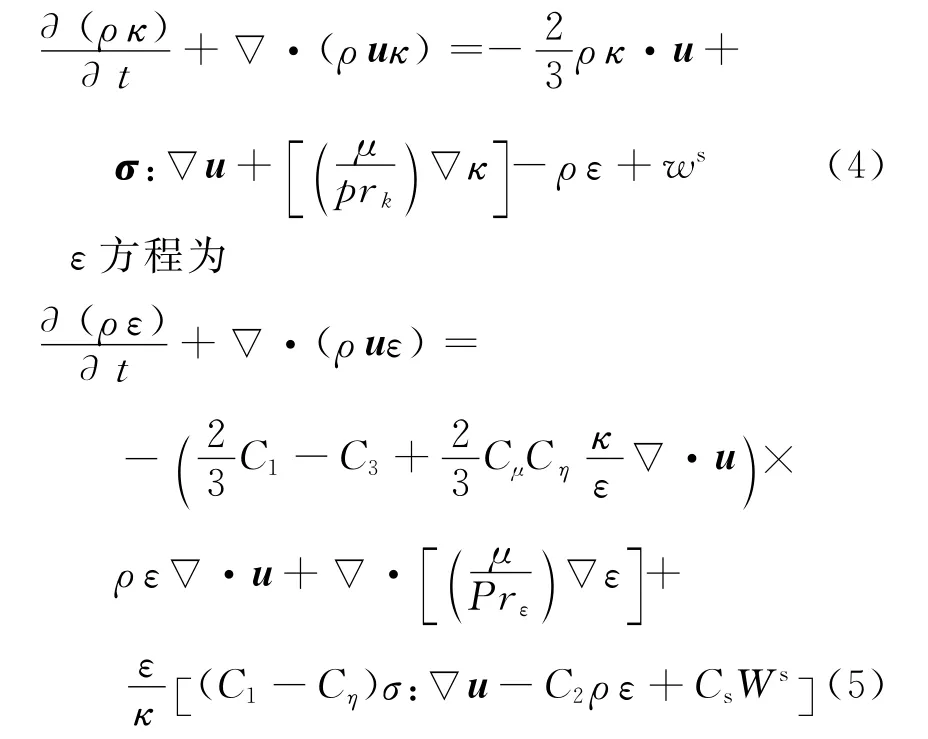
有关的详细方程论述可参考文献[4].
1.2 边界条件
本文计算区域的边界包括进出口边界和固体壁面边界.(1)进出口采用压力边界条件(入口压力为100kPa,出口压力为93kPa);(2)固壁边界:固壁的温度采用绝热边界,固壁的速度采用无滑移边界,边界层速度采用湍流壁面律边界.
2 气道几何模型的建立
模拟条件是基于AVL的发动机气道稳流实验条件,气缸长度为2.5D(D为缸径),网格:15万~20万个六面体结构化网格[5].由于气道阀口形状对流动很敏感,此区域属关键流域,建模一定要精确,故在气缸盖内和阀门附近对网格进行了加密.模型见图1.
3 KIVA动态网格的实现
与其他CFD软件不同,KIVA只需要发动机一个位置的网格即可实现整个循环的计算,活塞与气门运动过程中对网格的影响通过snap和rezone来调整,见图2.其中,snap:实现网格层的自动增加和删减;rezone:对气门运动引起的网格拉伸变形进行重整,保证网格的规则.
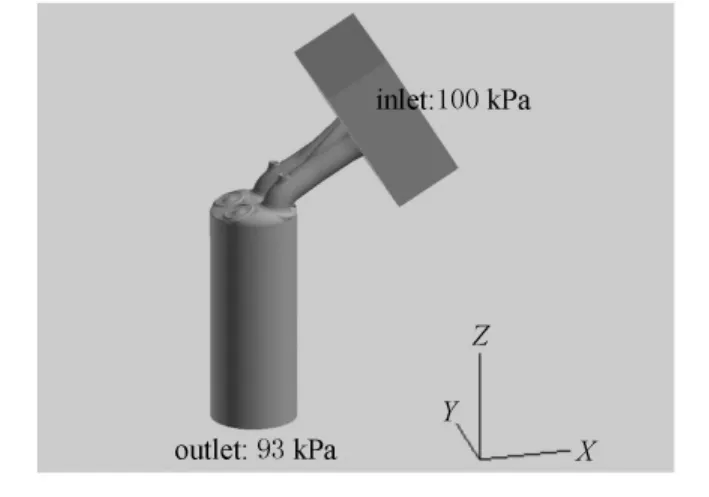
图1 几何模型

图2 动态网格的实现
应用 FAME[6-7]技术,自动生成六面体网格,气门与气缸套内壁最近点距离只有1.5mm,局部网格规模i×j×k为0.2mm×0.2mm×0.2 mm.气门升程1mm时,气门最小流通截面至少要有6层网格,以保证模拟计算时气流能够顺利流过此截面,此时局部网格规模i×j×k为0.1 mm×0.1mm×0.1mm.不同气门升程下(1~10 mm)分别对气道-气缸划分网格.
4 流量及流通系数的计算
4.1 流通系数
流通系数的定义为

式中:阻隔系数δ=Fv/FP;f为流量系数;mv为实际流量.理论流量为
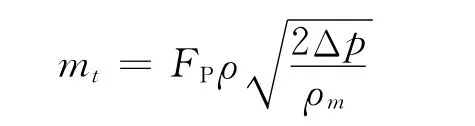
4.2 计算结果分析
图3分别是不同气门升程下进气道的流通系数随气门升程的变化曲线.由图知,随着气门升程的增大流通系数迅速增大.这是由于气门升程加大,流通面积增大和进气阻力的减小.当气门升程接近最大时,流通系数增加率变小,其主要原因是:此时气道与气缸的压差很小,同时气缸内滚流等气体运动强度却加大,进气阻力变大.

图3 不同气门升程流通系数变化曲线图
图4 为不同气门升程下气门轴线截面上的压力分布情况.图4a)表明,当气门刚开启时,在气门附近气道压力迅速下降,其原因是:此时气道与气缸存在巨大压力差.图4b)表明当气门升程加大,气道内压力急剧下降,气缸压力迅速上升,最终两者压力逐渐接近.在气门杆头部(即1处)和气门与气门杆连接处(即2处),气体受到阻滞,导致局部压力升高.
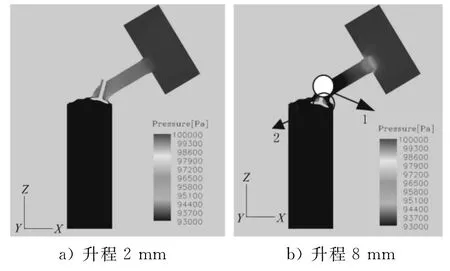
图4 不同气门升程气门轴线截面压力场
图5 为不同气门升程下气门轴线截面上的速度分布情况.由图5a)可见,当气门升程较小时,气体最大速度在气门喉口位置.气体进入气缸后,从气缸盖到气缸底速度逐渐减小,主要原因是气流进入气缸基本上都是绕气缸壁运动,越往下运动,气体受到的摩擦阻力就越大.由图5b)可见,在燃烧室与气缸盖的结合处(即3处),气体受到阻滞,气流的流动速度明显下降,气体流动变向.少量气流在气门迎风侧与缸盖之间(即4处)与被气门挡回来的进气交汇,形成高强度的湍流.在气流受阻部位,湍流能较大是减少充气量的重要原因.因此,应尽可能避免在此区域设计气道.
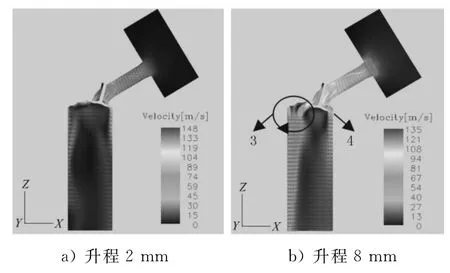
图5 不同气门升程气门轴线截面速度场
图6 为不同气门升程气缸中心线截面速度分布情况.图6表明,进气有很强的滚流,它有利于燃油和空气的混合.在进气门的下方(即5处)出现速度较低的“混合死角”,这不利于气体混合和燃烧的充分进行.

图6 不同气门升程气缸中心线截面速度场
图7 为垂直Z轴(缸盖下5.0mm处)的截面的速度分布情况.图7表明,由于结构上的对称性,气体进入气缸后,与缸壁相撞而挤向两侧,在水平截面上流场表现为对称分布、旋向相反的双涡结构.随着气门升程的增大,对称大涡逐渐破碎形成尺度更小、速度更大的涡,由此可以得出,进气道产生的涡流对缸内气体的混合有着明显的促进作用.
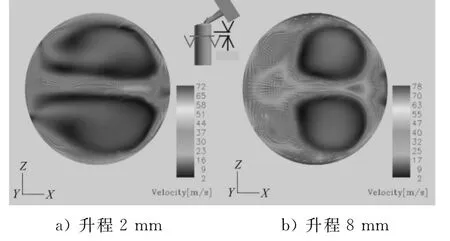
图7 垂直Z坐标截面速度场
5 不同数值模拟工具模拟结果的对比
由于缺少实验条件,故用Fire的模拟结果来比较.二者在相同的边界和模型条件下模拟计算的,结果见表1.由表1可知,KIVA的模拟结果与Fire的模拟结果基本相同.由于Fire计算网格数达70多万个,而KIVA的计算网格数才10多万个,故在计算成本上,KIVA有明显的优势.

表1 流量系数的KIVA模拟值与Fire模拟值的比较
[1]Bassem H.Ramadan numerical simulations in a high swirl methanol-fueled irectly-Injected nngine[J].SAE Technical Paper,2003(1):132.
[2]解茂昭.内燃机计算燃烧学[M].2版.大连:大连理工大学出版社,2005.
[3]顾维东,杨延相,蔡晓林,等.FAI二冲程直喷汽油机缸内流场多维数值模拟[J].内燃机学报,2007,25(2):152-155.
[4]魏明锐.二甲醚发动机的雾化理论和实验研究[D].武汉:华中科技大学,2004.
[5]陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2003.
[6]Laimbock F J,Meister G,Grilc S.CFD application in compact engine development[J].SAE Transactions,1998,107(3):1 998-2 004.
[7]Andras H,Zoltan H.Application of CFD numerical simulati on for intake port shape design of a diesel engine[J].Journal of Computational and Applied Mechanics,2003,4(2):123-128.
