κ－ε模型和RNG模型模拟分析车用空滤器湍流流场＊

刘志恩 尹 婧 颜伏伍 侯献军 郭晶晶

（武汉理工大学汽车工程学院1） 武汉 430070） （武汉软件工程职业学院2） 武汉 430205）

0 引 言

大多数车辆都是在多尘的环境条件下行驶，发动机工作时则极易吸入含有大量灰尘等杂质的空气，从而加剧内部零件的磨损，影响其使用寿命，空滤器的引入则可以较好的拦阻杂质，延长主要零部件的使用寿命，并改善发动机的动力性与经济性.

除了传统的实验方法，日渐成为趋势的CFD数值分析的使用也可以充分认识空滤器内流体的流动规律，并可以部分替代实验，大幅地减少实验研究工作量，从而降低研制费用和缩短开发周期，方便、灵 活、可 重 复 性 好［1－2］.本 文 采 用 FLUENT6.3.26软件，应用压力修正法中的SIMPLE算法、κ－ε湍流模型对某厂生产的空气滤清器的速度场和压力场进行模拟计算，并提出了改进方案，获得了良好的结果.

1 模型的建立及网格划分

空滤器系统由进出气管道和带有滤芯的滤清器壳体组成.应用UG软件建立空气滤清器内部流场的三维几何模型见图1.滤芯的形状及其所处位置见图2.

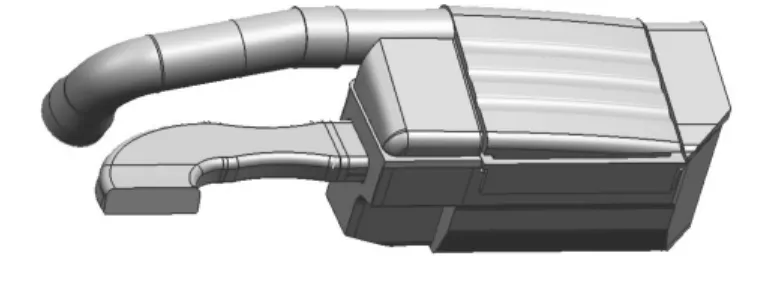
图1 空气滤清器计算域整体模型

图2 滤芯

空滤器工作时，气流从入口管道流入空滤器腔体，流动经过滤芯后，使空气中的尘埃被阻挡，或粘附在滤芯上，从而向发动机提供清洁的空气.

利用FLUENT前处理软件GAMBIT划分网格，由于此模型结构不规则，采用非结构四面体网格划分，并在入口管道流入壳体处及滤芯处局部细化，以此在尽可能减少网格数量的前提下提高计算精度，同时应避免网格过疏或过密.网格过疏会使计算结果产生偏差或迭代无法收敛；而网格过密则会大大增加计算成本.网格数量约为100万.2个相连的网格区域，在交接的地方设置成一对Interface边界，使不同网格的数据可以顺畅交接.网格模型如图3.

图3 计算域网格

2 数学模型

为了简化模型，作如下假设和简化：（1）空气密度变化很小，假设为不可压缩流体；（2）空气的物性与多孔介质（滤芯）的分布情况是各向同性的；（3）流体在空滤器中作定常流动；（4）稳定工况下，可认定整个流动过程为等温过程.

认为空气是粘性流体，取粘性系数μ为1.78×10－5Pa·s.

通过雷诺数来判断该流动为层流还是紊流［3－4］：Re＝1.37×105，即流动雷诺数大于上临界雷诺数，流动判定为紊流.选用高雷诺数κ－ε模型.近壁处的Re数较小，因此在近壁区域采用壁面函数法进行修正.

3 初始条件与边界条件设定

计算采用一阶迎风差分格式，方程求解采用SIMPLE算法.

入口边界采用速度入口边界.假设入口截面速度均匀分布，根据进气流量2 200m3／h，以及入口的横截面积0.024m2，经计算，设定速度为v＝25m／s.出口边界采用压力出口边界，给定压力的大小P＝0（相对大气压力）.固体壁面上的速度分量采用缺省的绝热无滑移边界，壁面速度为0m／s.

根据厄根公式［5－6］

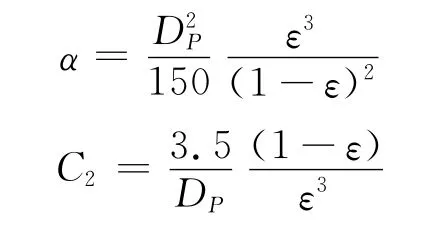
式中：Dp为球形颗粒的直径或非球形颗粒的体积当量直径，m；ε为孔隙率，分别在porous zone区域里设定.设孔隙率为0.8，粘性系数和惯性系数则分别设置为10kPa·s和1 000.

4 计算结果分析

4.1 速度场的分析

空滤器的速度流线如图4所示，可以清楚看到从入口进入的气体流入空滤器腔体后从出口流出的流动状态.少部分气体直接流入滤芯，从出口流出，大部分气体遇到与入口相对的壁面后产生较强的回流后，再流入滤芯进行过滤，所以靠近右侧腔体壁面的流线比较紊乱，而左侧腔体流线则比较稀疏.

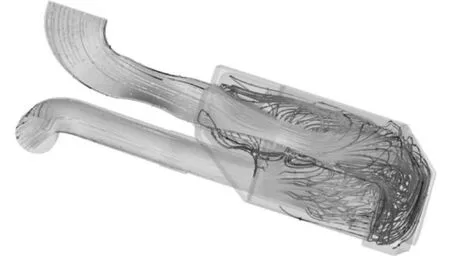
图4 空滤器流线图

选取两个具有代表性的中心剖面来更好的说明内部流场的流动状态.如图5所示，入口管道截面积突缩处，速度显著增大，是整个空滤器系统速度达到最大的地方，达到45m／s.管道突缩的设计可使得流体速度增大，从而充分均匀地流入空滤器腔体.入口管道和腔体的连接处的上拐角速度局部增大.贴近壁面的速度较小，对外壳冲击小.流体经过滤芯过滤后，阻力作用使流速明显减少，又因出口管道横截面积的减小，流速又相应增大.

图5 入口中心截面处速度矢量图

由于入口管道所处位置的影响，整个腔体气体流动不是很均匀，左侧腔体及滤芯左侧气体流入较少.经过滤芯的流体大部分从出口流出，但左半部分过滤效果不明显且流体不易流出，而右侧流动则相对均匀.

图6是流体进入滤芯的速度矢量图，从图6a）可看出，与左侧相比，滤芯右侧气体流入量较多且较均匀；图6b）则可显示入口截面左侧有较大的漩涡存在，使得流体流过的阻力较大.

图6 滤芯入口处速度矢量图

图7 ～8可看出空滤器腔体及滤芯多处有涡流，且流线弯曲程度较大，涡流加大了流体流动的压力损失.滤芯处的涡流会引起流动阻力的增加，流体不易流出，造成滤清效率的降低，缩短使用寿命.

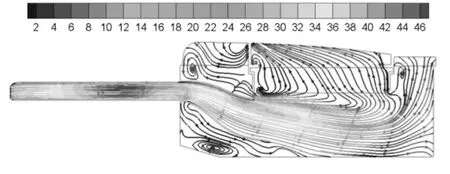
图7 入口中心截面处速度流线图

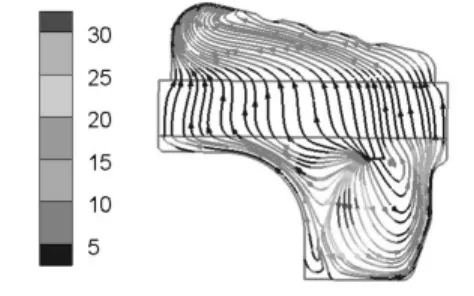
图8 滤芯纵向中心截面速度流线图

4.2 压力场的分析

入口管道压力先层层递减再有所提高，这是管道横截面面积的减小和增大所导致的，入口管道整体压降达600Pa左右.入口管道和腔体的连接处的上拐角处局部压力较小.腔体右侧的压力较高，是因为流体受到右侧壁面的阻挡产生冲击所导致，腔体从右至左，压力大致是减小的趋势，局部拐角处压力会小幅上升.而从图9b），c）显示，流体经过滤芯区域时，压力逐渐降低，压降达300Pa.

图9c）的压力云图显示，压力从下到上，基本是层层递减的，而在滤芯下方有一处因漩涡的存在而产生的低压区.（可参照图8）

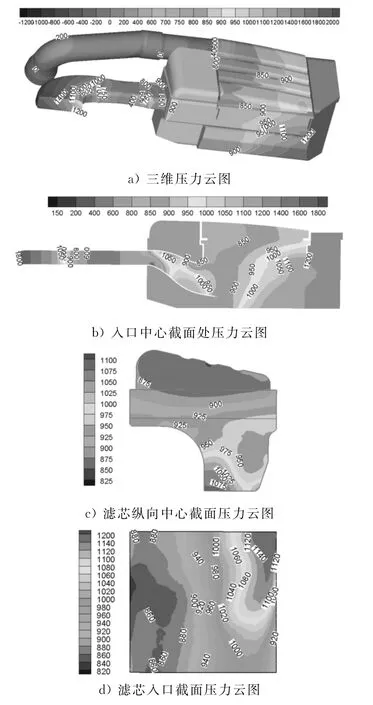
图9 空滤器压力云图

利用压差来评价空气流经空气滤清器的压力损失及阻力.经计算得，入口压力为1 488Pa，出口压力为3.3Pa，出入口压差约1.4kPa，压降较小.

4.3 应用RNGκ－ε模型计算

RNGκ－ε模型与标准κ－ε模型相比，采用了重正化群方法，修正了湍流黏度，考虑了流动旋转及旋流情况，在ε方程中增加了一个附加产生项，当流动快速畸变时，该项明显增加，反映了流的时均应变力，从而可以更好的处理高应变率及流线弯曲程度较大的流动.而从前文分析可知，本文所研究的空滤器流动的流线弯曲程度较大，故应用该湍流模型再次模拟计算.

利用RNG模型计算该模型，得入口压力为1 367Pa，出口压力为3.7Pa，压差约为1.3kPa.相关平面压力云图如图10所示，可看出压力变化趋势较为缓和.

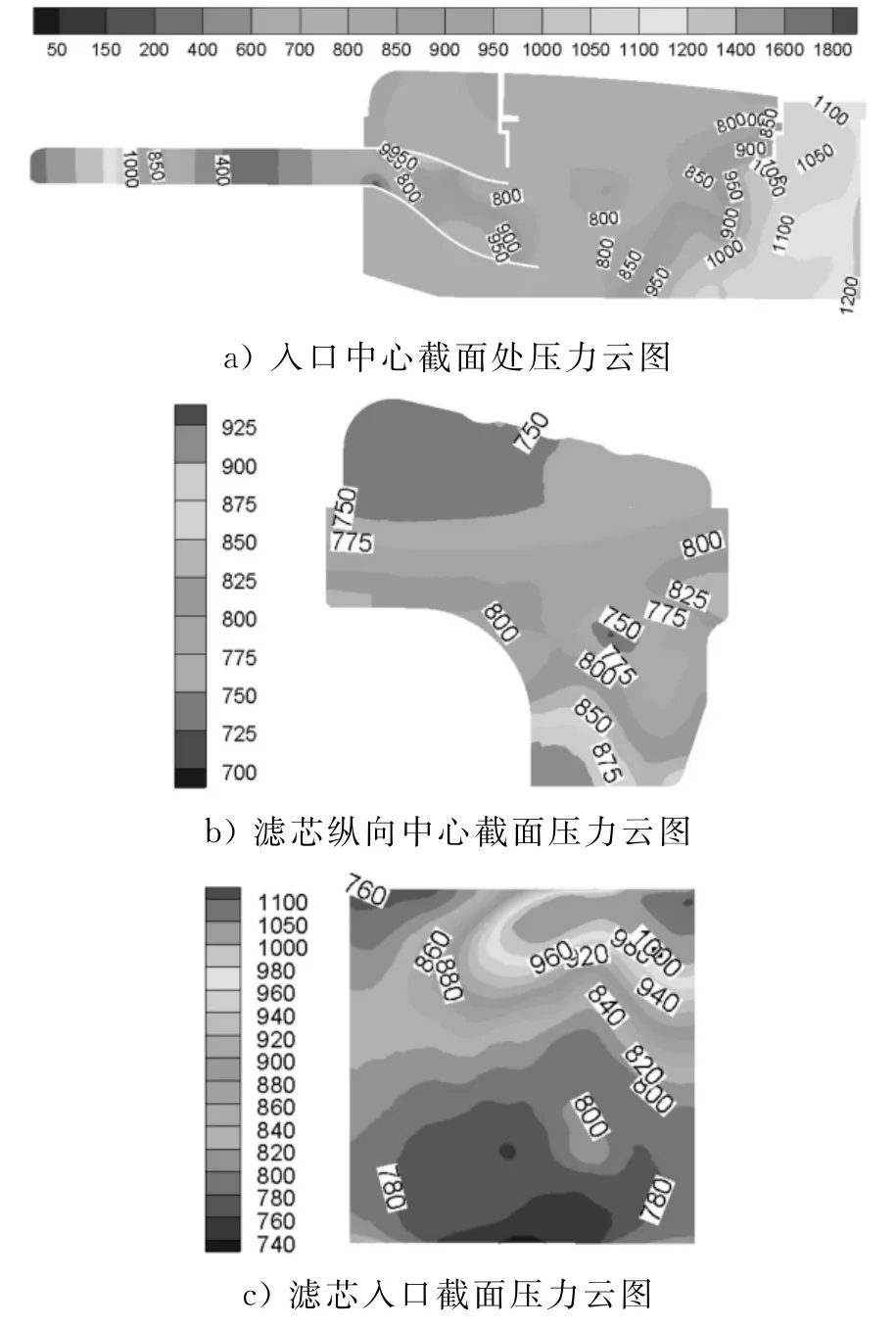
图10 RNG模型平面压力云图

从计算结果可以看出：原型空滤器的主要问题是腔体整体流动不是很均匀.腔体多处有漩涡，且由于进气管道与腔体交接位置的因素，左腔室流入的空气量较少；滤芯处流动也并不均匀，靠近入口处的位置，空气流入量较少，且有漩涡产生，引起流动阻力的增加，造成滤清效率的降低，缩短使用寿命.因此，改善空滤器结构的主要目的则是使滤芯处流动分布更为均匀.

通过以上分析提出改进方案：改变空滤器入口管道的位置，使流入气体更好的与滤芯接触，从而提高滤清效果.将入口偏离滤芯位置增加8mm，见图11～12.

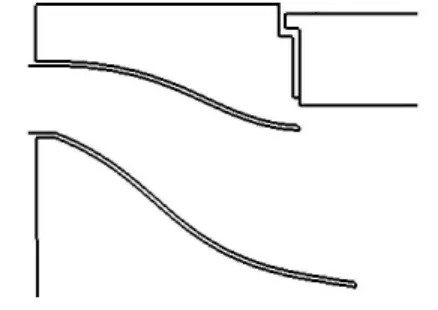
图11 原型入口位置

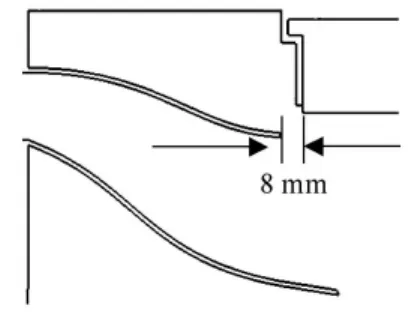
图12 改进后的入口位置

由图13～14可看出，滤芯左下角的漩涡明显减小，可有更多的流体均匀经过滤芯，提高了滤清效果.而空滤器腔体内，漩涡数量减少且位置有所转移，流体流动达到一定的改善.进出口压差值则依旧维持较小值，变动不大.图15与图9d）对比可看出，改进型的滤芯入口压力分布更为均匀，左处的涡流影响较小，流动更顺畅.

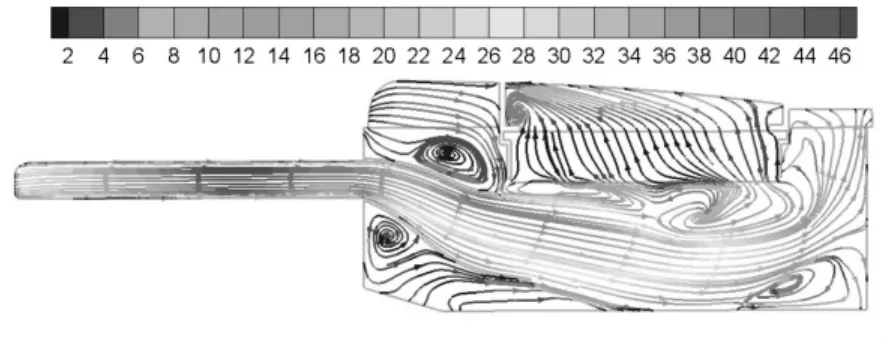
图13 改进型流线图

图14 改进型速度矢量图

图15 改进型滤芯入口横向压力云图

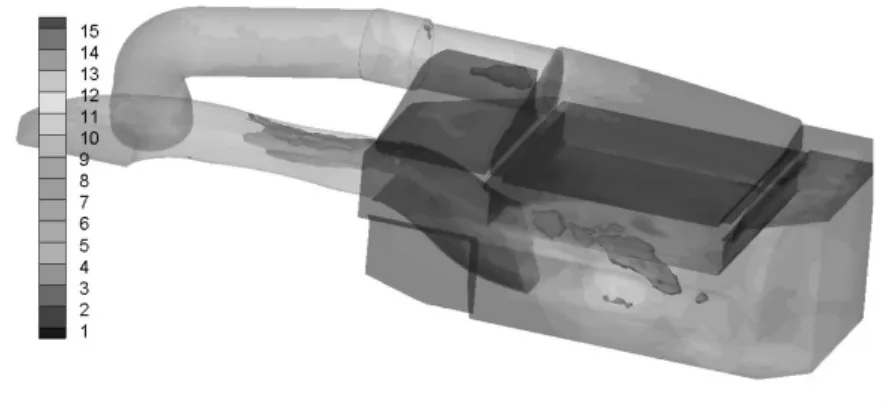
图16 改进型湍动能分布

5 结 论

1）速度最大处出现在入口管道的突缩区域；管道突缩的设计可使流体能以较大的速度流入空滤器腔体，从而使流动充分到整个腔体.

2）空滤器腔体整体流动较均匀，几处有漩涡，且由于进气位置的因素，左腔室流入的空气量较少，滤芯处流动也并不均匀，靠近入口处空气流入量较少，且有漩涡产生，引起流动阻力的增加，造成滤清效率的降低，缩短使用寿命；因此，需改善空滤器结构使流动分布均匀.

3）空滤器入口管道、多孔介质区域产生明显的层层压降，背压达到1.3kPa左右，压降较小.

4）提出新的改进方案，将入口管道向左平行偏离原位置8mm，使流动更为均匀，可以有更多的流体可通过滤芯，从而提高空滤器的滤清效率.

［1］贾彦龙.基于三维紊流数值模拟的空气滤清器结构优化设计［D］.济南：山东轻工业学院机械工程学院，2008.

［2］韩占中.FLUENT流体工程仿真计算实例与分析［M］.北京：北京理工大学出版社，2009.

［3］王 伟，王仁人，张 良.基于CFD的内燃机空气滤清器内气固两相数值模拟［J］.德州学院学报.2010，26（2）：77－81.

［4］陈庆光，徐 忠，张永建.RNGκ－ε模式在工程湍流数值计算中的应用［J］.力学季刊，2003，24（1）：88－95.

［5］Nagarajan G，Kumar S M E，Chowdhury D G R.CFD analysis of air filters for an off－highway vehicle［J］.SAE Paper，NO.2007－26－048.

［6］Cesareo de La Rosa Siqueira，Martin Poulsen Kessler，Fabio Moreira，et al.Three－dimensional numerical analysis of flow inside an automotive air filter［J］.SAE Paper，NO.2006－01－2629.