RBCC可重复使用运载器上升段轨迹优化设计①

龚春林，韩 璐

(西北工业大学航天学院，西安 710072)

RBCC可重复使用运载器上升段轨迹优化设计①

龚春林，韩 璐

(西北工业大学航天学院，西安 710072)

针对火箭基组合动力(RBCC)可重复使用运载器(RLV)轨迹多段、多控制变量、推力与飞行轨迹耦合，飞行轨迹设计困难的问题，提出了基于高斯伪光谱方法的数值优化求解模型和求解方法，并获得满足要求的上升段燃料最省轨迹。将该轨迹分为3部分，分别由引射火箭、亚燃冲压和超燃冲压发动机提供动力，以攻角和燃料秒流量为控制变量，根据轨迹任务和各模态发动机启动及工作条件建立优化模型、设定各段末端和路径约束，利用高斯伪谱法求解最优轨迹并利用特殊方法计算边界控制变量。通过与传统方法所得轨迹的对比表明，所建立的优化模型和方法可快速求解出RBCC运载器上升段最优轨迹，优化结果符合RBCC运载器工作特点。

火箭基组合动力;轨迹优化;高斯伪谱法

0 引言

火箭基组合动力装置(Rocket Based Combined Cycle，RBCC)可充分利用大气层中氧气而无需携带氧化剂，可大幅提高运载器载荷系数，综合比冲是现有火箭发动机的数倍，使人类更加廉价、频繁地进入太空成为可能，在空间运载领域备受关注。

相对传统的火箭动力，RBCC是复杂的吸气式动力装置，它综合了引射火箭(Ejector)、亚燃冲压(Ramjet)、超燃冲压(Scramjet)等模态，其工作性能与飞行状态相互影响，且工作范围较宽，推力变化较大，这就决定了RBCC运载器的运载能力与轨迹设计关系更为密切，且轨迹设计约束更为严格和复杂。为了提高运载器载荷系数，就必须尽可能减少上升过程所消耗的燃料。但为了最大程度发挥RBCC优势，得到上升段燃料最省轨迹，传统运载器轨迹设计经验和规律已难以胜任，采用基于最优控制理论的优化设计方法是必然趋势。

国外在论证RBCC运载器时，主要通过POST和OTIS飞行轨迹优化程序进行优化设计［1］，但由于并非为RBCC飞行器特别设计，未能考虑RBCC工作特点，在计算过程中易出现不合理的RBCC发动机性能计算状态。国内对RBCC飞行器的研究尚处于起步阶段，对其轨迹研究大多停留于方案的可行性研究，而对最优轨迹的求解方法研究不足。文献［2］给出了基于马赫数-动压参考曲线的RBCC飞行器爬升段轨迹设计方法，虽然考虑了发动机性能与飞行状态之间的相互影响，但未采用优化方法，因此无法获得最优解;文献［3］对固体运载火箭上升段分段轨迹优化进行了研究，但由于火箭发动机不存在启动条件约束问题，因此未引入段间交接条件约束，其模型也无法用于RBCC飞行器的轨迹优化。

本文以某亚轨道RBCC运载器为对象，针对以上描述的该类飞行器轨迹设计特殊问题，建立以全程攻角和燃料消耗量为控制变量的优化设计模型，并基于高斯伪光谱方法，建立以燃料最省为目标的优化求解模型，通过某飞行器算例验证方法并与采用传统方法所得轨迹进行对比，以证明其优越性。本文的研究旨在结合RBCC飞行器的特点建立优化设计方法、优化建模思路和分析结论，为这类新型飞行器的轨迹设计提供可行的途径。

1 问题描述

RBCC运载器作为第一级助推器，其任务剖面如图1所示。

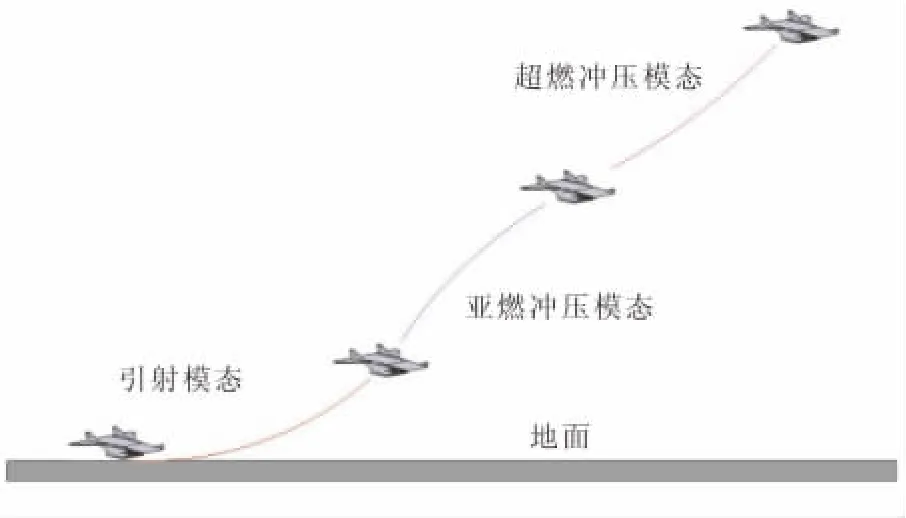
图1 RBCC运载器上升段轨迹任务剖面图Fig.1 The profile of ascent trajectory of RLV powered by RBCC

采用水平方式起飞，经引射、亚燃、超燃3种工作模态，将有效载荷运送至临近空间，然后返回。决定其运载能力的主要是上升段，包括4个阶段:

(1)起飞离地阶段。在引射火箭发动机工作下，从静止加速至起飞速度。

(2)引射模态加速及爬高阶段。该阶段从离地状态加速至亚燃发动机的接力条件。引射发动机的比冲和推力较小，其轨迹设计难点在于如何尽快爬高和加速，尽早转入高比冲的亚燃阶段，避免长时间的低空阻力消耗。提高爬高速度可通过增大飞行攻角实现，但同时会增大飞行阻力，减小加速度。因此，攻角规律的选择必须在二者之间权衡。

(3)亚燃模态加速及爬高阶段。该阶段发动机比冲最高。其设计矛盾在于:从加速角度，提高燃油喷注量可提高发动机推力，有利于加速，但同时发动机比冲降低;从爬高角度，如果爬升过快，则发动机进气量下降，比冲和推力降低;如爬高过慢，由于大气密度高、阻力太大，同样影响飞行器性能。

(4)超燃模态加速及爬高阶段。该阶段工作高度和速度较高，轨迹设计的矛盾与亚燃阶段相似。

另外，对各模态转接问题，吸气式发动机的启动条件给运载器的飞行状态提出了严格限制，同时由于各模态发动机在马赫数等方面的工作范围存在重叠，因此，必须根据各模态特点和飞行状态，合理确定各模态转接点。

通过以上分析可知，RBCC运载器的飞行轨迹和燃料消耗量的确定受到的约束条件非常苛刻，必须在诸多约束之间权衡协调。目前尚没有其他确定该类飞行器攻角和燃油调节规律以使燃料最省的方法，必须通过优化设计的手段实现。

2 优化问题建模

2.1 状态方程

影响飞行器性能的主要是纵向平面内轨迹，因此飞行器状态方程可通过以下二维方程统一描述:

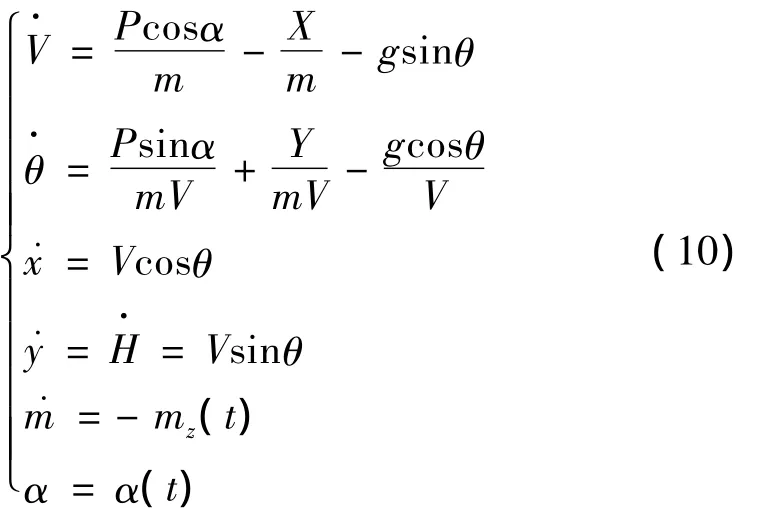
式中V、θ、x、H、m、α、mz分别为飞行速度、轨迹倾角、航程、高度、质量、攻角和燃料秒消耗量;P=Ispmz为发动机推力，Isp为发动机比冲，与马赫数Ma、α、H密切相关。

对于不同工作模态，Ma、α、H燃油当量比φ对比冲的影响规律不同，计算表达式为

式中Isp，e(·)、Isp，r(·)、Isp，s(·)分别为引射、亚燃、超燃状态下的比冲插值表，由发动机性能分析或试验给出。

升力Y和阻力X的计算公式:

式中S为飞行器参考面积;CX和CY分别为阻力系数和升力系数，根据攻角和马赫数插值而得。

飞行过程中动压计算公式:

驻点热流峰值计算公式:

式中 ρ为大气密度，kg/(km)3;C为常数，取3.008;R为驻点处曲率半径，取0.25 m，速度单位km/s。

2.2 优化模型

2.2.1 优化指标

选择在满足给定任务指标的前提下，最小燃料消耗作为优化指标:

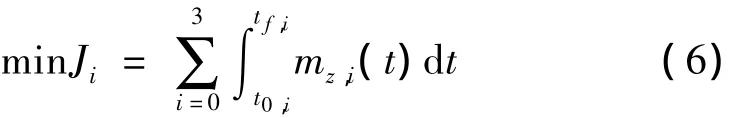
式中t0，i为第i阶段终止时间;tf，i为第i阶段终止时间。

由于各段连续工作，有

2.2.2 设计变量

对本文研究的RBCC运载器，攻角变化规律和油量调节规律决定了飞行轨迹，且这2个参数对载荷能力影响很大。因此，选择攻角和燃料秒消耗量作为控制变量。同时，吸气式发动机工作要求飞行器攻角范围不能太大，且燃料消耗也需在一定范围内。综上，设计变量可描述为

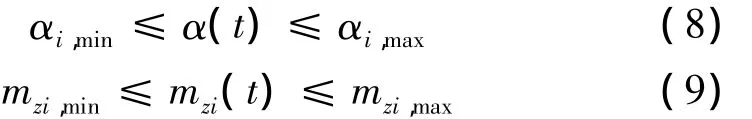
αi，min、αi，max、mzi，min、mzi，max与各阶段发动机工作模态有关，通过发动机工作包络性能分析获得。

2.2.3 状态变量

状态变量包括速度、轨迹倾角、航程、高度、质量、动压和驻点热流峰值等。设S为状态变量，则根据轨迹任务要求，可将状态变量路径约束和边界条件约束分别描述为

2.2.4 发动机启动条件

飞行状态直接决定吸气式发动机能否顺利启动，将吸气式发动机启动条件转换为模态切换点处攻角和马赫数约束:

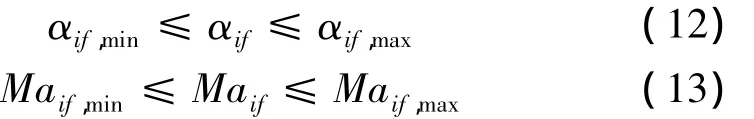
3 基于高斯伪谱法的求解方法

在轨迹优化理论中，数值解法一般分为直接法和间接法［4-5］。对非线性系统而言，采用间接法求解两点边值问题时，需估计出没有物理意义的协态变量初值，这一缺陷制约了间接法的应用。直接法采用离散最优化逼近最优控制，将最优控制问题转化成参数优化问题，从而避免了对协态变量初始值的估算，大大降低了求解最优控制问题的难度，因此本文采用直接法。高斯伪谱法(Gauss Pseudospectral method，GPM)是直接法的一种，适合RBCC飞行器轨迹优化求解。

3.1 高斯伪谱法的求解思路

高斯伪谱法将未知的状态变量和控制变量在一系列高斯点上离散，并以这些离散点为节点构造拉格朗日插值多项式来逼近状态和控制变量。通过对全局插值多项式求导，来近似状态变量对时间的导数，将最优控制问题转化为具有一系列代数约束的参数优化问题，即非线性规划问题(NLP)［6-7］。

3.2 连续最优控制问题的离散

采用高斯伪谱法，需将轨迹优化问题的时间区间［t0，tf］转换到［-1，1］，对时间变量t作变换:

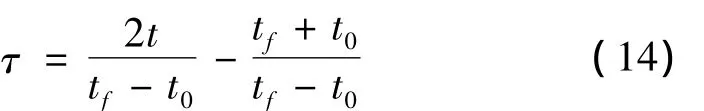
高斯伪谱法取K阶勒让德-高斯(LG)点以及τ0=-1作为节点，构成K+1个拉格朗日插值多项式，并以此为基函数，构造状态变量和控制变量的近似表达式，即

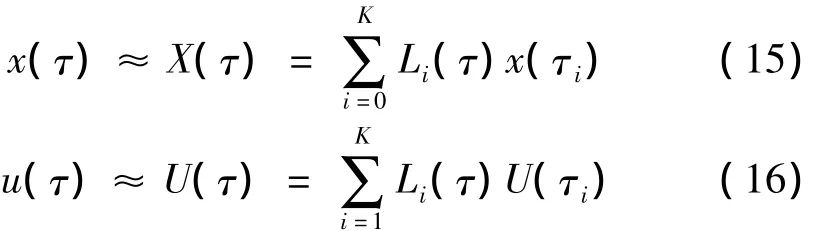
对式(15)求微分有:

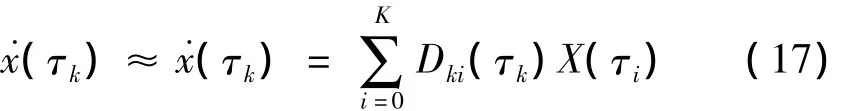
从而将微分方程动态约束转换为一系列代数约束:

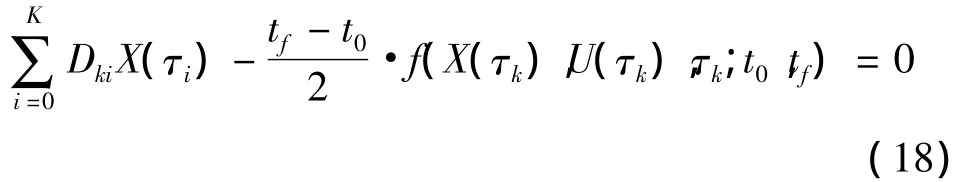
其中，k=1，…，K。

将终端约束条件离散，并用高斯积分来近似:

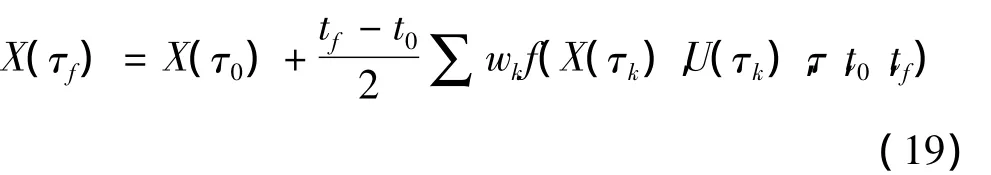
性能指标可由高斯积分近似为

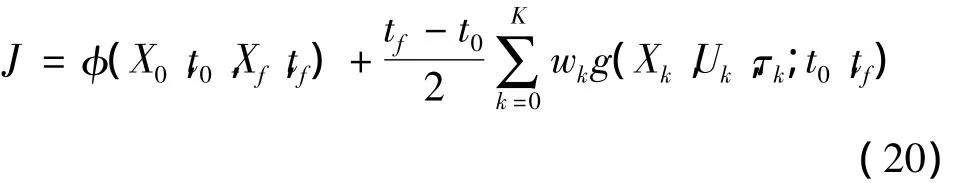
边界条件变为

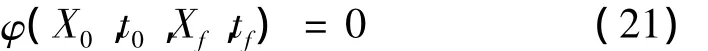
路径约束为

其中，k=1，…，K。

3.3 边界控制变量处理方法

高斯伪谱法控制变量仅在LG点处离散，因此而得的NLP问题无法合理处理边界处控制变量。但本文中各阶段末端攻角为下一阶段吸气式发动机启动条件之一，因而要求必须合理求解各阶段末端控制变量。为此，本文基于Huntington的工作采用如下方法求解边界控制变量。

由于边界处不考虑最优控制问题的路径约束，考虑Hamilton函数不含路径约束的形式:

将路径约束引入可行控制变量集合:

式中U是τ0时刻控制变量的所有可行解集合;C0是该时刻满足路径约束的控制变量集合。

这样对控制变量的求解转换为对如下约束优化问题的求解:

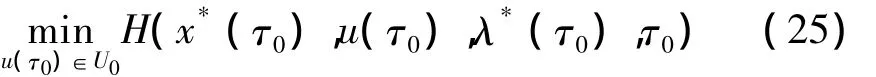
该方法适用于初始及终端控制变量的求解。

4 算例

4.1 算例描述

某RBCC运载器的任务是将一定质量的载荷运送到35 km的目标高度，Ma≥8。该运载器采用乘波体外形，设计起飞质量为50 t，从地面水平起飞。

RBCC各模态工作范围为引射模态Ma为0～3，亚燃冲压模态Ma为1.5～6，启动时要求攻角位于-2～3°范围内;超燃冲压模态Ma取5以上，启动时要求攻角位于-1～1°范围内。该运载器使用液氢燃料，全程燃料流量可调。引射模态下攻角变化范围为-5～15°，亚燃和超燃模态时均为-2～2°;各模态燃料消耗量变化范围均为150～200 kg/s，要求最终燃料消耗不超过20 t。全程要求动压不大于2.5×105N/m2，驻点热流峰值不大于6.0×105W/m2。求解过程中，各段轨迹间存在耦合，耦合形式为上段轨迹末端状态作为本段轨迹的初始状态。

4.2 状态变量约束设定

根据第2节建立的优化模型和该飞行器的任务要求，其状态约束条件如表1、表2所示。

表1 状态变量初始及终端约束设定Table 1 The initial and terminal constraint of state variables

表2 状态变量路径约束设定Table 2 The path constraint of state variables

4.3 计算结果

根据传统的轨迹设计经验，引射阶段由于推力小阻力大，大攻角离地之后，在保证足够升力的前提下应尽快减小攻角;为节省燃料，燃料流量除了在起飞离地和跨音速阶段需要保持较大值之外，其余均应限制在较小值。亚燃和超燃模态由于推力较大，保持小攻角和较小燃料流量飞行，不但可减小阻力损失和保持较好的进气条件，且可保证较大的爬升速度。另外，在确定模态转接条件时，应当尽可能增加比冲最大的亚燃冲压发动机的使用范围。

计算结果如图2～图10所示。图中未标记的曲线是根据设计经验，采用传统实验设计方法，经过大量计算、耗费大量机时设计出的上升段轨迹，是所计算的大量可行轨迹中燃料消耗最少的。用“GPM”标记的则是采用高斯伪谱法获得的燃料最省轨迹曲线，曲线上所标记的点便是LG点和边界点。图中“E-R”表示引射模态与亚燃冲压模态切换点;“R-S”表示亚燃冲压模态与超燃冲压模态切换点。

4.4 结果分析

由质量变化曲线可知，在满足所有约束前提下，采用传统实验设计方法所得轨迹消耗燃料19.6 t，而采用高斯伪谱法所得轨迹消耗燃料17.7 t，节省燃料达9.7%，且爬升所需时间更短。

图2 攻角变化曲线Fig.1 The history of angle of attack

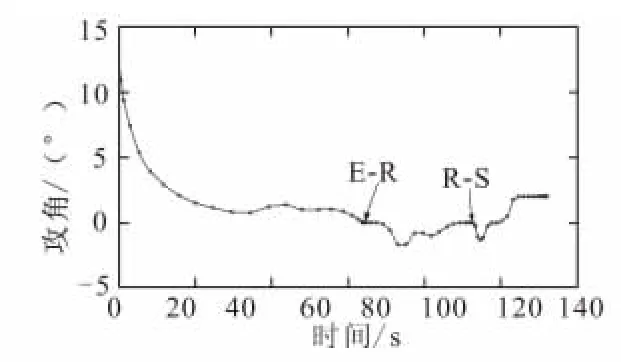
图3 攻角变化曲线(GPM)Fig.3 The history of angle of attack(GPM)

图4 燃料流量变化曲线Fig.4 The history of fuel flow

图5 燃料秒流量变化曲线(GPMFig.5 The history of fuel flow(GPM

图6 马赫数变化曲线Fig.6 The history of Mach number

图7 轨迹曲线Fig.7 The curve of trajectory

图8 质量变化曲线Fig.8 The history of mass

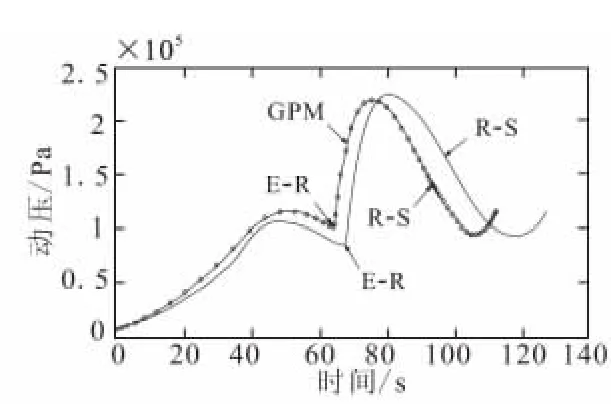
图9 动压变化曲线Fig.9 The history of dynamic pressure

图10 驻点热流峰值变化曲线Fig.10 The history of heating of rate stagnation point

由计算结果可知，引射模态推力较小，在该阶段初期应将能量主要用于加速，以使飞行器拥有较大的爬升初速度，之后将能量更多用于爬升，以尽快脱离大气对流层;亚燃模态阶段推力大、阻力小，应尽可能减小攻角使速度和高度快速提升;超燃模态下，高斯伪谱法与传统方法所得结果有着明显区别，由于该阶段推力大、高度高、阻力小，应适当增大攻角和燃料流量，在提高速度的同时，使高度也能快速增加，以减少所需时间和燃料消耗。在亚燃和超燃模态转接处，攻角出现一定幅度变化，这是由于将模态间切换视为瞬间完成，在亚燃和超燃模态切换时，由于比冲突然减小，且空气阻力较小，因此采用减小攻角的方法来减小重力在加速过程中的不利影响，此处攻角变化速度为1.9°/s。模态交接马赫数分别为1.5和6，在飞行过程中，应尽可能增加推力较大、效率较高的亚燃冲压发动机的使用时间。

5 结论

(1)根据优化结果分析可知，优化后得到的燃料/攻角联合调节规律符合RBCC运载器各阶段工作特点，因此所建立的优化模型是合理的。

(2)针对RBCC运载器多段、多控制变量、动力与飞行轨迹耦合等特点，利用高斯伪谱法以及对边界控制变量的特殊求解方法，可快速求得满足所有约束和指标的上升段燃料最省轨迹，并通过与传统方法所得轨迹的对比，证明该方法可大大减少燃料消耗，在RBCC运载器轨迹设计上具有巨大的优越性。

(3)通过优化分析，引射模态消耗的推进剂约占全过程消耗推进剂的55%，是决定爬升过程中推进剂质量消耗的关键;亚、超燃冲压发动机推力大、效率高，应尽可能增加整个飞行过程中冲压发动机使用范围。

［1］Doug N.Qualitative and quantitative assessment of optimal trajectories by implicit simulation(OTIS)and program to optimize simulated trajectories(POST)［R］.Georgia:Georgia Institute of Technology，2001.

［2］吕翔，何国强，刘佩进.RBCC飞行器爬升段轨迹设计方法［J］.航空学报，2010，31(7):1331-1337.

［3］杨希祥，张为华.基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究［J］.宇航学报，2011，32(1):15-21.

［4］Biegler L T.An overview of simultaneous strategies for dynamic optimization［J］.Chemical Engineering and Processing;Process Intensification，2007，46(11):1043-1053.

［5］雍恩米，唐国金，陈磊.基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化［J］.宇航学报，2008，29(6):1766-1772.

［6］周文雅，杨涤，李顺利.利用高斯伪谱法求解具有最大横程的再入轨迹［J］.系统工程与电子技术，2010，32(5):1038-1042.

Optimization of ascent trajectory for RBCC-powered RLV

GONG Chun-lin，HAN Lu
(College of Astronautics，Northwestern Polytechnical University，Xi＇an 710072，China)

Since the multi-phase and multi-control-variable trajectory of the reusable launch vehicle(RLV)which is coupled with the thrust powered by rocket based combined cycle(RBCC)is difficult to solve，the numerical optimization model and method based on Gauss Pseudospectral Method(GPM)were proposed，and the optimal-fuel ascent trajectory was obtained.The trajectory is divided into three phases powered by rocket，ramjet and scramjet in sequence.The angle of attack and fuel flow are control variables，and according to the trajectory mission，the ignition and work condition of the each mode，the optimization model was built，the terminal and path constraints were imposed.The optimal trajectory was solved by using GPM and the boundary control variables were solved by a special method.Compared with the result by traditional method，the optimization model and GPM can solve trajectory optimization problems effectively，and the optimal result accords with the characteristic of the RBCC-powered RLV and satisfies all the constraints.

RBCC;optimization of trajectory;Gauss pseudospectral method

V421.1

A

1006-2793(2012)03-0290-06

2011-11-03;

2011-12-05。

武器装备预研基金(9140A20100111HK0318);西北工业大学毕业设计重点扶持项目。

龚春林(1980—)，男，副教授，研究方向为飞行器总体设计。E-mail:leonwood@nwpu.edu.cn

(编辑:崔贤彬)