涡流阀变推力发动机推力计算方法①

金 蔚，李 江，魏祥庚

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

涡流阀变推力发动机推力计算方法①

金 蔚，李 江，魏祥庚

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

针对目前理论模型多注重可行性和影响因素分析，以及方程复杂求解困难的现状，为了得到一个应用性较强的涡流阀变推力发动机推力工程计算方法，借鉴普通固发求解推力原理，结合数值模拟方法，建立了涡流阀变推力发动机的整体模型。结果表明，该模型有一定的精度，模型计算参数与试验和前期理论分析趋势一致，模型简洁并包含主要设计参数，可满足涡流阀变推力发动机的设计需要。

固体火箭发动机;涡流阀;推力;工程计算方法

符号说明:

0 引言

在过去所研究的多种固发推力调节方案中，涡流阀法是实现固体火箭发动机推力调节的一种有效方式，它通过向发动机流场切向喷入流体，迫使燃气发生旋转，增大主流来流阻力。对于采用指数燃速形式装药的固体火箭发动机来说，燃烧室压强会改变，进而达到推力调节的目的［1］。涡流阀法具有其独特的优点，它是一种不带活动部件的流体控制元件，具有流量调节的功能。目前，国内外针对涡流阀及其在固体火箭发动机上的应用进行了原理性试验，建立了初步理论模型，通过研究证明了涡流阀法用于固体火箭发动机进行推力调节的可行性。国防科大刘冰等采用数值模拟方法进行了涡流阀方案对流量调节可行性研究，张为华等进行了固体火箭发动机推力调节的涡流阀方案研究，得到涡流阀流量调节特性，并通过试验实现了一定推力比［2］;西北工业大学余晓京、魏祥庚等分别采用数值模拟和试验的方法进行了涡流阀变推力发动机性能影响因素的研究［3-4］。Lewellen 等［5］早期对喷管内超音速旋流流动分析，并建立了理论模型，为涡流阀内流场分析奠定基础;Walsh在20世纪70年代较早将其理论部分用于涡流阀发动机内进行理论分析［6］，以后国内主要分析依据大多来源于此。

涡流阀变推力发动机的调节性能最直接和最重要的体现就是调节前后推力比和压强比，所以准确计算调节后燃烧室压强和推力直接影响发动机性能估算和设计。但由于影响涡流阀变推力发动机性能的因素较多，且各因素强烈耦合，所以目前的理论模型多偏重于可行性和变化趋势分析，模型实际应用性不足。现在尚没有一套用于涡流阀固体火箭发动机上准确可行的推力计算公式。因此，本文在已有理论分析基础上，以涡流阀发动机设计为宗旨，建立了涡流阀变推力发动机的推力工程计算方法。

1 推力计算模型

1.1 涡流阀变推力发动机推力计算模型

涡流阀结构和部分结构参数见图1。

涡流阀变推力发动机调节性能最直接和最重要的体现为调节后压强比和推力比;如果要求解调节后压强和推力，同样必须先采用类似于普通固体发动机中推导平衡压强公式的方式，通过质量守恒确定主燃烧室压强，进而将调节前后推力式作对比，从比值关系式中通过已知量确定比值，从而得到调节后推力。

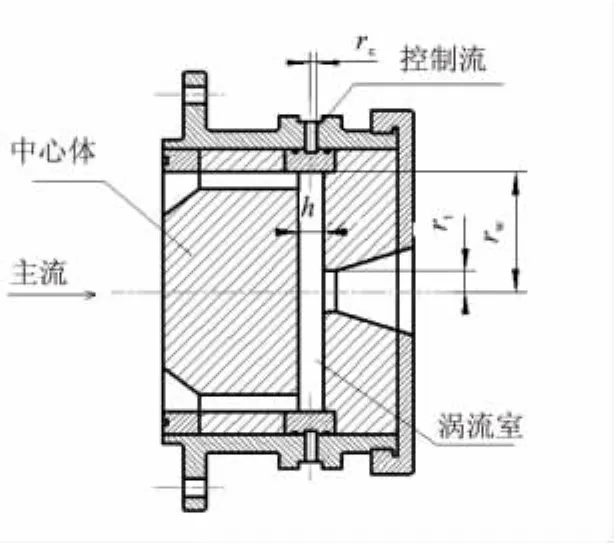
图1 涡流阀结构示意图Fig.1 Schematic diagram of vortex valve

因此，调节后燃烧室压强是首先要确定的，但目前还没有一种公认的以简洁合理形式确定涡流阀内喷管质量流率的方法，发动机内流量关系还需采用能包含主要设计参数的无量纲化的关系式进行拟合。

在早期Lewellen等对喷管内超音速旋流流动分析所建立的理论模型中，一个重要方面就是提供了W0、Wc和主要设计参数之间的关系［5］。

于是，涡流阀性能可通过W0、Wc和Ws来表示:

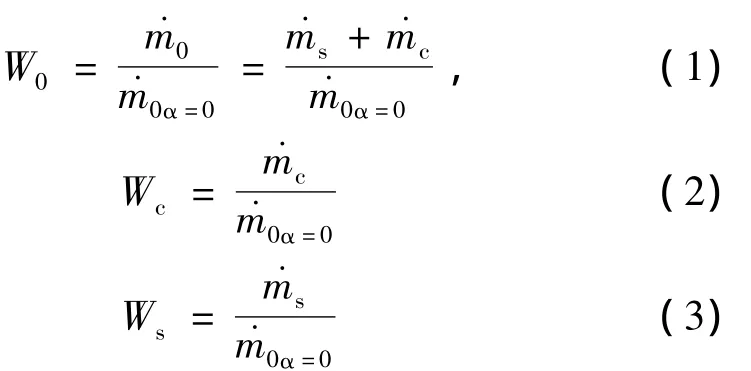
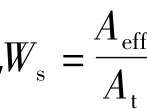
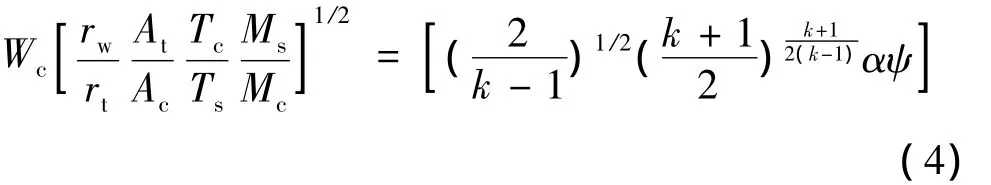
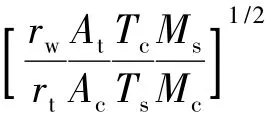
1.1.1 求解调节后主燃烧室压强

(1)控制流流量

综合考虑动量交换和比冲损失，目前认为要达到较好的调节效率且工作稳定，2个对称分布控制流喷孔是一个基本标准，所以研究主要针对2个喷嘴。故控制流流量为

控制流流量由控制流气体滞止参数、背压(主流压强)及喷孔面积Ac决定。

(2)主流流量

主流流量达到壅塞时，对于给定固体装药，质量流率直接由燃烧室压强决定。

(3)主流壅塞质量流率

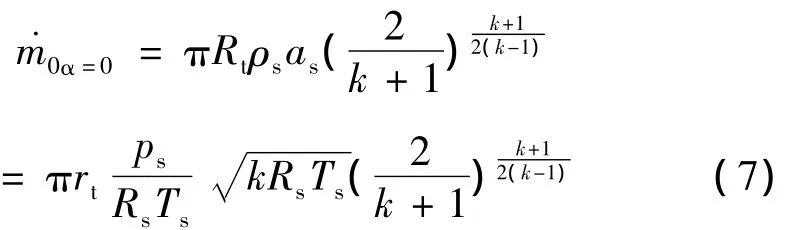
代表同等主燃烧室压强下无旋转主流壅塞质量流率，并以其对主流、控制流和经喷管流量进行无量纲化。

(4)经喷管总质量流率无量纲化

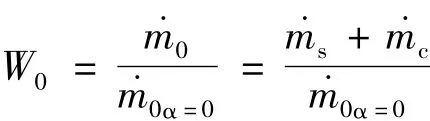
(5)控制流质量流率无量纲化

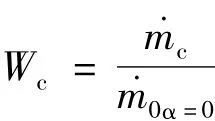
方程中ps为待求未知量，方程闭合仅缺少Wc和W0关系式。

1.1.2 求解调节后推力

当发动机已处于稳态的条件下，根据固体火箭发动机推力计算公式变形有:

当无控制流时:

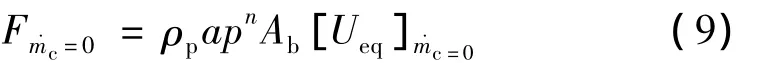
当喷入控制流后:

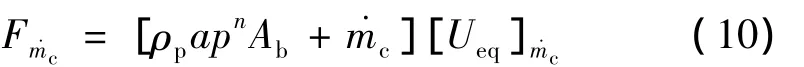
控制流的主要效应是减小有效喉部面积，进而影响燃烧室压强;其中，Ueq影响是次要的［7］:

(c)涡流阀发动机是以小流量控制流较大幅度调节主流，其以质量加权平均计算的掺混后燃气总温、相对分子质量和比热容比参数更接近于主流，在推力计算中暂时不考虑掺混引起其变化，均以主流参数代替。

所以，有以下合理假设:

则推力比为

在求解调节后主燃烧室压强后，调节前后推力比根据式中参数已可确定，进而结合调节前推力、调节后推力可求解。

对于整个方程中现在唯一缺少W0和Wc关系式，而目前其还无法根据给定装药和构型参数直接确定，表达式中旋流强度仍无法根据已知参数确定。所以，目前只能通过拟合方式得到。为得到更多数据，本文采用数值模拟的方法进行拟合。

1.2 数值计算结果分析与拟合处理

1.2.1 数值模拟计算模型及边界条件

对于高速旋转流动计算过程的复杂性和研究问题的侧重点，需在不破坏主要物理现象和物理量的条件下进行适当假设，即假设流动过程无化学反应;壁面为绝热无滑移固壁。

数值模拟在Fluent 6.3中完成，采用的控制方程为雷诺时均N-S方程、湍流模型为sst-kω模型［8-10］，计算过程选用耦合算法。

边界条件设置:(1)主流入口采用质量通量入口，并引入模拟真实固体火箭发动机流量随压强变化过程的UDF;(2)2个控制流入口采用压力入口，给定入口总压;(3)出口为压力出口;(4)壁面采用绝热无滑移固壁。

主燃烧室压强计算结果与试验结果对比见表1。

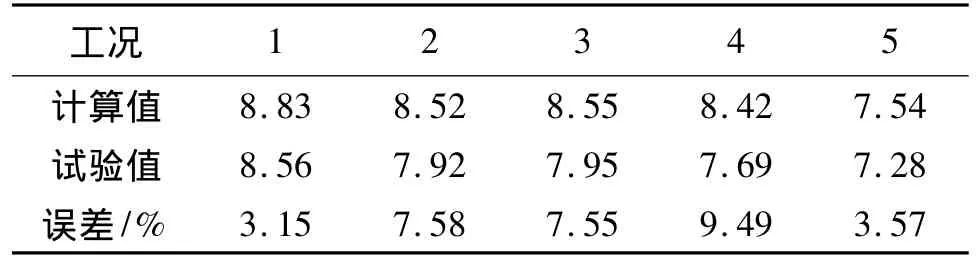
表1 主燃烧室压强计算结果与试验结果对比Table 1 Chamber pressure comparison of test and numerical results MPa

计算结果和实验数据在一定程度上吻合较好，误差在10%以内，说明计算结果具有一定精度，可用于涡流阀内流场的分析计算，而其误差可能由于热损失、旋流损失等引起。

1.2.2Wc和W0拟合方法

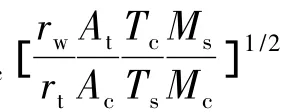
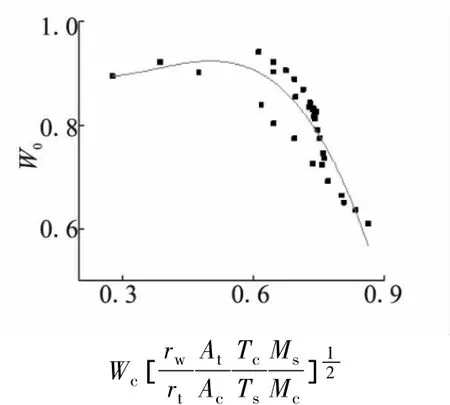
图2 多项式拟合曲线Fig.2 Nonlinear curve fitting

分别采取较常用的指数拟合、对数拟合和多项式拟合等拟合方式，其中多项式拟合结果能较好地代表数据趋势，有较宽的求解范围。图2为采用多项式以现有数值计算结果进行拟合曲线，其拟合式为

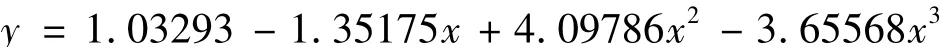
以多项式拟合的计算式，可计算控制流压强范围在9 MPa以上的燃烧室压强。说明采用多项式拟合方式，可实现较宽的适用范围。所以，对于较高的控制流压强，此拟合式具有一定适用性。但众多拟合方式难以取得不受限制的拟合式，对于9 MPa以下情况难以求解。所以，考虑采用分段函数的方法进行拟合。

对9 MPa以下采用其他方式拟合，拟合结果为y=0.93 × |x-0.617 98|0.00268，其中x＜0.617 98，方程可求解。

2 模型计算结果与分析

以某涡流阀变推力发动机为例，控制流为氮气，计算不同工况下发动机燃烧室压强和推力。使用试验工况选取比例因子中有关参数如下:

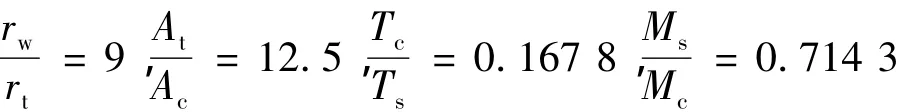
采用多项式拟合的关系式要有实用性，必须可对调解后压强和推力进行准确计算，并能预示参数和性能变化趋势。

图3和图4分别为调节后主燃烧室压强和发动机推力随控制流压强的变化。结果显示，计算结果和试验数据具有较好的一致性。由于理论模型未考虑附面层、粘性耗散和传热的影响，调节后模型计算压强和推力均略大于实验值;调节后推力误差在10%内，且试验和模型比值保持较强规律性，考虑在最终结果中加入系数修正，即Freal=0.908 7F。

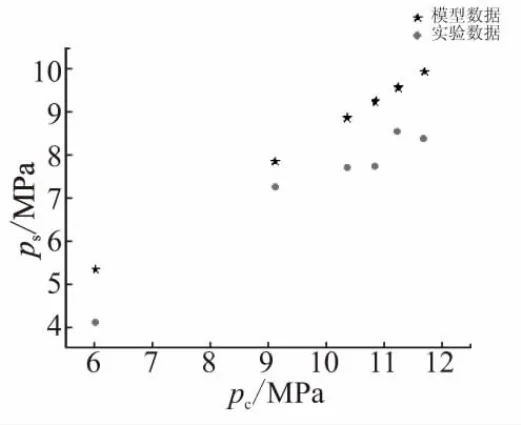
图3 主流压强随控制流压强Fig.3 psvs pc

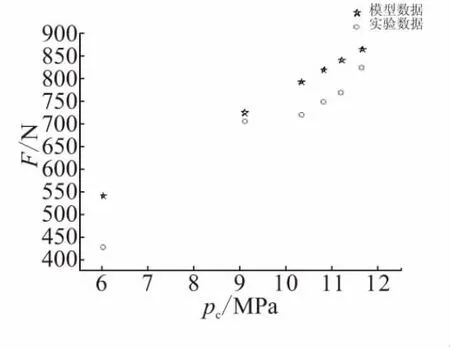
图4 推力随控制流压强变化Fig.4 F vs pc

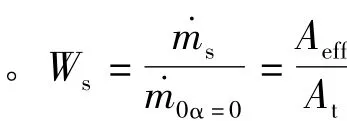
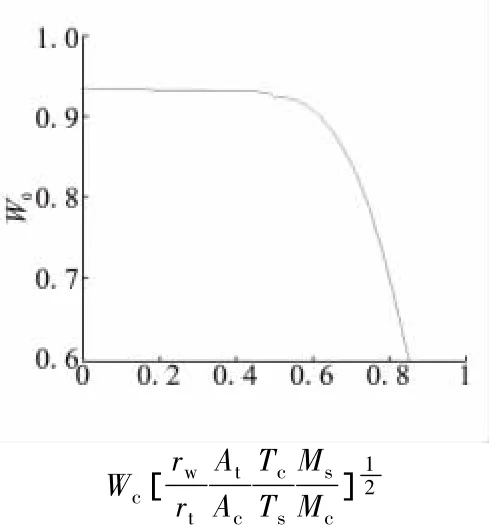
图5 W0和Wc关系Fig.5 W0vs Wc

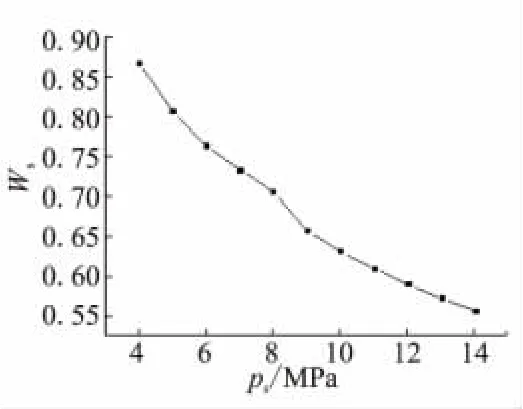
图6 ps和Ws关系Fig.6 psvs Ws

3 结论

(1)计算模型计算所得的压强和推力与实验数据相比具有一定精度，且计算所得参数趋势和以往理论分析相对应，表明本文计算模型可用。

(2)结合已有分析模型，建立了计算涡流阀变推力发动机调解后推力的简化方程，较简洁的计算式能包含主要的结构设计参数，实现了根据装药和构型对性能预估，以及通过性能要求进行发动机设计。

［1］徐温干.固体火箭发动机推力大小调节技术的发展［J］.推进技术，1994，15(1).

［2］张为华，程谋森，刘分元.固体火箭发动机推力调节的涡流阀方案研究［J］.推进技术，1995，16(5).

［3］魏祥庚，何国强，李江，等.涡流阀几何参数对固体火箭发动机推力调节性能的影响［J］.推进技术，2007，28(4).

［4］余晓京，何国强，李江，等.涡流阀式变推力发动机性能影响因素数值研究［J］.西北工业大学学报，2009，27(2).

［5］Lewellen W S，Burn W J，Strickland H J.Transonic swirling flow［J］.AIAA Journal，1969，7(7):1290-1297.

［6］Walsh R F，Lewellen W S，Stricker D B.Investigation of a solid propellant rocket motor modulated by a fluidic vortex valve［R］.AIAA 70-643.

［7］Greenberg I，Wolff H.Cold flow evaluation of parameters influencing thrust modulation by a fluidic vortex valve［J］.Israel Journal of Technology，1975，13:73-81.

［8］Yu Xiao-jing，He Guo-qiang，Li Jiang，et al.Numerical analysis of flow in variable thrust SRM［R］.AIAA 2007-5801.

［9］Ray-Sing Lin，Nathan Hartford.Analysis of fluidic vortex valves for airflow control in combustors［R］.AIAA 2002-2646.

［10］Alon Gany，Marat Mor，Claudio Goldman.Analysis and characteristics of choked swirling nozzle flows［J］.AIAA Journal，2005，43(10).

Thrust calculation method of variable thrust SRM controlled by vortex valve

JIN Wei，LI Jiang，WEI Xiang-geng
(Science and Technology on Combustion，Internal Flow and Thermal-structure Laboratory of Northwestern Polytechnical University，Xi＇an 710072，China)

In order to solve the problem that most theoretical models focus on feasibility and effect factors analysis，a compact thrust calculation method of variable thrust SRM controlled by vortex valve was put forward.The calculation results obtained by the model agree well with test results.The model is simple and involves main design parameters，which satisfy the design requirement for variable thrust SRM controlled by vortex valve.

solid rocket motor;vortex valve;thrust;engineering formula

V430

A

1006-2793(2012)03-0330-05

2011-12-21;

2012-02-15。

金蔚(1985—)，男，硕士，研究领域为航空宇航推进理论与工程。E-mail:jhputin2004@163.com

(编辑:崔贤彬)