一种高精度MEMS梳齿驱动器有限元仿真方法及实验

郭占社 ， 曹 乐 ， 赵 鑫 ， 樊尚春

（1. 北京航空航天大学仪器科学与光电工程学院，北京 100191；2. 精密光机电一体化教育部重点实验室，北京 100191）

微机械静电梳齿驱动器自1989年由Tang[1]等提出以来，由于具有结构简单、与集成电路工艺兼容等优点而在微机电系统中得到了广泛应用。尤其在航空航天领域，MEMS梳齿驱动器已经成为 MEMS惯性器件如加速度传感器[2]以及MEMS陀螺[3]最主要的驱动源以及弱信号检测的手段。

目前，国内外对MEMS梳齿驱动器的研究，大多都是利用理想情况下的计算[4]得到的，即认为计算过程中电场的边缘效应可以忽略不计。然而，由于实际利用 MEMS工艺制作梳齿电容过程中加工工艺的限制，导致梳齿间的深宽比相对较小，在此情况下，电容的边缘效应已不可忽略[5-7]。因此，欲得到高精度的计算结果，必须对其理想模型进行重新评估，以得到较精确的计算结果。

本文利用有限元分析方法中的能量法，提出了一种基于能量法的对梳齿驱动器电容量进行高精度仿真计算的方法，实验证明，相对于其它常用的电容仿真方法[8-10]，此方法具有较高的计算精度。

1 微机械梳齿驱动器工作原理

典型的微机械梳齿驱动器结构示意图如图1所示，它主要由可动梳齿、固定梳齿、支撑梁、锚点等4部分组成。可动梳齿与支撑梁相连接，固定在锚点上。测试过程中首先在驱动端施加一电压V，由于静电梳齿驱动器电容极板间静电力作用，驱动器可动梳齿沿 X方向会产生一定位移，使得检测端梳齿交叠面积发生变化，使电容量C也随之发生变化。通过检测电容量的变化，便可实现对位移的检测。

图1 梳齿驱动器结构示意图

可见，电容量的精确计算对于 MEMS传感器中梳齿驱动器的性能研究及设计具有重要意义。

2 梳齿电容驱动器有限元仿真方法

一般地，梳齿电容计算采用理想模型进行计算，该公式中电容可表示为

其中，ε为介电常数，a为梳齿宽度，b为相邻梳齿的重叠长度，d为相邻梳齿间距，n表示组成梳齿驱动器的极板电容的对数。

然而，由于 MEMS制作工艺限制，导致梳齿电容极板的深宽比较小，此时，边缘效应已不可忽略。由于影响电容量的因素比较复杂，所以欲推导出真正符合计算要求的理论模型十分困难，而有限元仿真技术正是解决这一问题有效手段之一。

2.1 常用仿真方法

一般地，有限单元法对梳齿电容计算大多是采用CMATRIX宏命令进行的。该方法能进行多元模拟求得多导体系统自电容和互电容，并能把对地电容矩阵变换成集总电容矩阵，以便用于电路仿真。但对 MEMS梳齿驱动器的研究通常不关心其自、互电容和电容矩阵，而是期望得到直观的电容量数值。所以用CMATRIX对驱动器进行电容提取会给研究带来很多不必要的麻烦，在进行复杂模型的相关计算时对试验机器硬件要求较高，且精度较低。因此，该方法虽能给出参考结果，但并不能完全胜任梳齿驱动器的电容检测仿真分析工作。

2.2 能量法进行电容有限元仿真

鉴于针对梳齿驱动器的电容检测仿真分析方法的现状，本文提出利用被熟知的能量和电容的关系来对研究对象进行电容提取。计算过程中首先利用有限元软件计算出在极板施加电压后电容器每一个节点的能量 Ei施加驱动电压后电容器所有节点的能量之和。该结果可表示为

其中n表示有限元网格中结点个数，n越大，得到的计算精度越高。

于是，由能量与两极板间电势差及电容量间的关系

式中V1和V2分别表示施加于两个极板的电势，we是静电场能量，C为电容，得到电容表达式为

2.3 能量分析法在MEMS梳齿驱动仿真中的应用

为验证该方法的测试精度，利用有限元软件Ansys，对利用MEMS工艺制作的硅微机械陀螺上用于质量块驱动的静电梳齿驱动器电容进行了仿真计算，器件实物图如图2所示，图中梳齿共 180个，材料为单晶硅， 仿真过程中材料相关机械参数如表1所示。

表1 材料特性参数表

图2 MEMS 陀螺显微图片

建立得到的有限元模型如图3所示，模型中相关尺寸即采用实际加工完毕后的数值，其具体数值如表2所示。

图3 梳齿电容驱动器有限元模型

表2 梳齿驱动器的尺寸数据 ( µm )

采用能量法，计算得到平板电容电场分布如图4所示，由图可以看出，在MEMS梳齿驱动器边缘，电场强度仍然具有较大的数值，表明MEMS梳齿驱动器的边缘效应是不可忽略的。

图4 电场分布模拟仿真结果

计算得到的各节点能量之和为1.91×10-11J。把该结果代入式（4）得到该梳齿驱动器中电容计算结果为1.5283 pF。

同样，对相同梳齿驱动器，运用前述CMATRIX法计算得到的结果为1.5793 pF。

利用公式（1），采用相同的尺寸及材料参数，可得到在忽略边缘效应及制作工艺条件下该梳齿驱动器电容量理想值为1.27pF。

可见，由于考虑了边缘效应的影响，采用能量法以及CMATRIX法得到的结果都比采用理想公式得到的结果大得多。而采用能量法得到的计算结果更接近于理想计算结果。

3 实验验证

为进一步比较能量法以及CMATRIX法的计算精度，利用高精度 LCR测试仪，对在同一工艺条件下，一个加工批次制作的硅 MEMS陀螺质量块上的梳齿驱动器的电容量进行了测试。为减小测试过程中的偶然误差，测试共选取了3个样品，并对每个样品进行了3次测试。

利用高精度LCR设备测试得到的结果如表3所示。

表3 梳齿驱动器电容量测量值 (pF)

依据误差理论与数据处理相关知识，得到电容量平均值

可见，相对于理想计算结果，实验结果同样具有较大的数值。该测量结果与本文提出的能量法的基于ANSYS的电容检测仿真计算得到的结果间的相对误差为

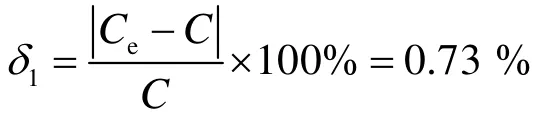
同样，对相同梳齿驱动器，该测量结果与利用CMATRIX方法比较得到的相对误差为

式中 Ce和 Cm分别表示利用能量法以及CMATRIX法得到的电容量计算结果。可见，相对于CMATRIX法，采用能量法能够得到更加准确的计算结果。

4 结 论

本文提出了一种基于能量法的对梳齿电容驱动器电容量进行高精度仿真计算的方法并利用 Ansys软件实现了该方法。然后，以 MEMS陀螺上的静电梳齿驱动器为研究对象，对其电容量进行了仿真计算。利用该方法及常用的CMATRIX法得到的计算结果分别为 1.5283 pF和1.5793 pF。该计算结果与利用高精度LCR测试仪测得的电容值1.5172 pF之间的相对误差分别为0.73%和4.09%。实验结果表明，该方法具有较高的计算精度，能够满足相关运算的需求。

[1]Tang W C, Nguyen T H, Howe R T. Laterally driven polysilicon resonant structures [C]//Proc IEEE Micro Electro Mechanical Systems, 1989: 53-59.

[2]Monajemi P, Ayazi F. Design optimization and implementation of a microgravity capacitive HARPSS accelerometer [J]. IEEE Sensor Journal, 2005, 6(1):39-46.

[3]Acar C, Shkel A M. Inherently robust micromachined gyroscopes with 2-DOF sense-mode oscillator [J].Journal of Microelectromechanical Systems, 2006,15(2): 380-387.

[4]McDonald G A. Review of low cost accelerometers for vehicle dynamics [J]. Sensors and Actuators A, 1990,21(1-3): 303-307.

[5]Jiang Tao, Wang Anlin, Jiao Jiwei, et al. Detection capacitance analysis method for tuning fork micromachined gyroscope based on elastic body model [J]. Sensors and Actuators A: Physical, 2006,128(1): 52-59.

[6]董林玺, 车录锋, 王跃林. 梳齿的不平行对电容式微机械传感器可靠工作范围的影响[J]. 半导体学报,2005, 26(2): 373-378.

[7]赵 剑, 王洪喜，贾建援. 计及边缘效应的静电驱动微结构静电力计算[J]. 微纳电子技术, 2006, (2):95-97.

[8]牛 刚, 贾志海, 王 经. 基于ANSYS的多极板电容传感器仿真研究[J]. 仪器仪表学报, 2006, (2):280-284.

[9]李锦明, 郭慧芳, 刘 俊. 一种三框架电容式硅微机械陀螺结构设计与仿真[J]. 传感技术学报, 2008,(2): 258-260.

[10]李燕斌, 邵可然, 雷 刚. 静电梳齿驱动器静电结构耦合的仿真分析[J]. 华中科技大学学报, 2009,37(2): 96-99.