基于拉普拉斯网格变形的三维植物叶片建模

苗 腾 ， 赵春江， 陆声链， 郭新宇

（1．中国农业大学信息与电气工程学院，北京 100083；2．国家农业信息化工程技术研究中心，北京 100097）

植物器官的真实感建模与绘制方法是计算机图形学领域的研究热点，其中对于叶片的绘制更是重中之重。植物叶片的形态具有多样性、不规则性的特点，如何逼真地模拟其结构特征和形态细节是一项巨大的挑战。植物叶片三维建模的应用需求主要来自两方面：一是作为影视动画以及游戏的自然场景元素，二是农学研究中作为虚拟农业试验的虚拟实验对象。在动画和游戏制作领域，对于形态结构细节的精细程度要求不高，更多的是考虑模型的视觉效果以及绘制过程的实时性。而对于农学研究来说，仿真结果需要真实地反映器官的生理特征和品种特性，所以生成的模型要达到较高的精细度。

L系统作为通用的植物拓扑结构描述语言，在植物模拟中应用较广，很多研究也将其应用到叶片的建模中[1-2]，但是对于具有随机边缘的结构，生成的结果单调呆板。一些学者利用边缘轮廓构建叶片的模型[3-4]，这类方法交互性强，可以设计任意外形的叶片，但是对叶片的自然弯曲等细节的表达存在缺陷。文献[5]提出了利用真实三维数据重构叶片的方法，可以得到自然界中叶片的真实形态，但是操作过程十分复杂。除了对叶片几何形态的描述研究之外，一些学者还从叶片纹理[6-7]以及光照[8-9]等方面对叶片进行模拟，在像素空间得到了很好的真实感。一些学者也注意到，植物叶片具有丰富的形态结构，利用上面的方法难以进行如卷曲、萎蔫等特定形态的植物叶片建模，并提出了专门的方法[10]。但这些方法的操作过程都比较复杂，交互设计不够自然。

本文提出了一种新的植物叶片三维形态交互式设计方法，利用拉普拉斯变形技术对叶片曲面进行交互式编辑，从而达到设计各种形态的三维植物叶片造型的目的。实验证明，本方法可以快速构建植物叶片的三维模型，同时对真实叶片的细节特征保持较好，避免了失真。

1 叶片曲面轮廓特征点的获取

本文以黄瓜叶片为例，说明特征点获取过程。

图1 利用Fastscan三维扫描仪探笔进行数据采集

利用三维扫描仪Fastscan获取叶片的轮廓中轴点数据，如图1所示。用Fastscan的探笔点取需要获得的轮廓点以及叶脉主脉中轴点（本文采用黄瓜叶片的主叶脉作为中轴线），只获取少量具有明显特征的点即可，这样将大大减少采集数据时的工作量。在点取过程中，需要分别记录下左、右轮廓以及中轴上选取点的数量，以便系统可以对数据进行分类。如有需要，可以在Fastscan配套的软件Polhemus里查看、编辑点信息。

除了利用扫描仪获得轮廓中轴点数据外，还可以基于叶脉形态特征计算这些点信息。叶脉形态特征是通过叶脉实测数据的统计学规律总结出来的，为此进行了一系列的数据采集并作统计学分析。选生长均匀一致的 15株进行取样，在每株的同一叶位上选取叶片进行数据采集，这样选取的叶片生理年龄基本相同。将叶片尽量展平直至可以近似为平面，测量特征较明显的一级叶脉数据（长度以及角度）。如图 2，测量 OA、OB、OC、OE、AF、CG、DI、BH的长度，以及∠COA、∠EOC、∠DOE、∠BOD、∠OAF、∠OCG、∠ODI、∠OBH的角度值。为方便分析，对叶脉进行编号，OE为1号叶脉，OD +DI为2号，OB+BH为3号，OC+CG为4号，OA+AF为5号。

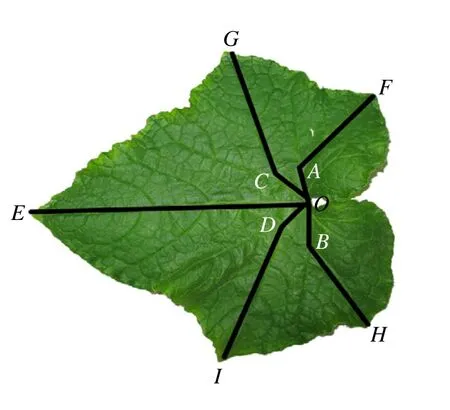
图2 测量叶脉数据

得到数据之后，对其进行处理，首先处理长度数据。设OE为1，对其他叶脉长度数据做归一化，得到各个叶脉长度之间的比例系数，之后计算比例系数的相关性，发现数据间的相关性较高，所以将得到的比例系数近似作为叶脉长度之间的比例因子，这样在系统中只需要输入叶脉OE的长度，就可以近似得出其他的叶脉长。相关性数据如表1所示。之后处理角度数据，对角度值按区间进行划分，选取出现概率最大的角度范围作为各个角度的取值范围。

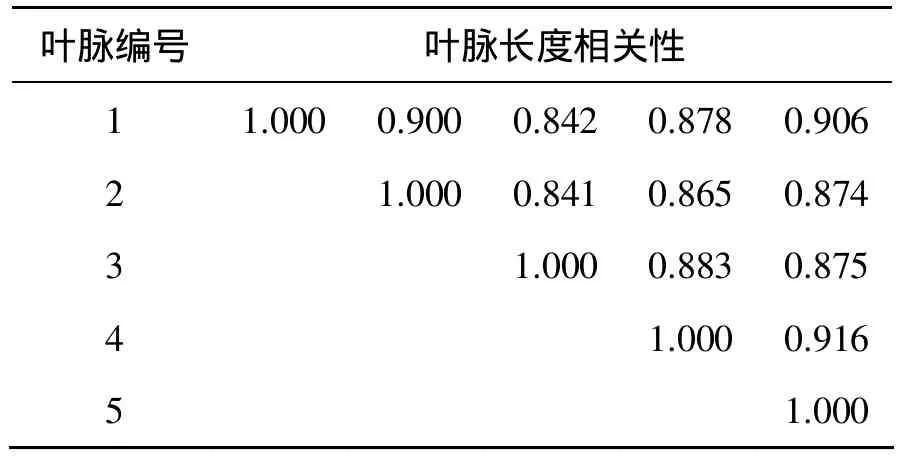
表1 各编号叶脉长度数据相关性

计算出叶脉长度以及角度值之后，可以根据二维平面几何简单地计算出叶片关键特征点E、G、F、H、I的位置，之后再根据各个点之间的边缘形态特征计算出轮廓点，如EG之间用直线拟合，FO之间用二次曲线拟合。为了避免呆板，在拟合中会加入适当的随机处理。而中轴上的点只需要在OE线段上选取即可。

本方法支持手动添加并调整轮廓中轴点的功能。用户可以在操作界面上添加点信息，也可以随意拖动点，这样可以较灵活的修改曲面信息。图3为交互编辑数据点的操作过程。

图3 交互编辑数据点

2 叶片曲面网格生成

以轮廓点以及中轴点为控制点，利用三次样条插值曲线分别拟合出左、右轮廓线以及中轴线，之后按照一定的间隔在轮廓以及中轴线中获得一系列的采样点；将左右轮廓采样点分别与中轴采样点顺次相连形成多边形，然后根据DeWall算法[11]实现三维空间中不规则多边形的三角化。为了使曲面更加光滑，可以对曲面进行细分，本文采用自适应细分方法[12]进行细分。

获得三角网格之后，计算每个点的纹理坐标。本文简单的将叶片曲面投影到一个二维平面，然后与叶片纹理做映射。该二维平面通过主成分分析方法计算，计算步骤如下：

1）计算所有顶点的重心坐标；

2）构建离散度矩阵，并通过离散度矩阵计算协方差矩阵；

3）对协方差矩阵进行特征分解；

4）其中最大特征值对应的特征向量为第1主成分，第2大特征值对应的特征向量为第2主成分；

5）第1主成分向量和第2主成分向量组成的平面确定为该二维平面。

真实世界中，黄瓜叶片的正反面是不同的，为了模拟这种情况，本文渲染时绘制两遍曲面，第1次绘制时开启背面剔除，并映射叶片正面纹理；第2次绘制时开启正面剔除，映射叶片背面纹理。这样会大大增加叶片的真实感。

3 叶片曲面的变形计算

本文采用拉普拉斯变形方法对叶片曲面进行变形。拉普拉斯方法速度较快，能够达到实时交互，而且其交互性比较简单，用户可以在三角网格上选取一系列操作点，然后拖动任意一个操作点，之后整个曲面中非操作点将产生变形，而操作点尽量保持不变。同时，拉普拉斯方法在保持网格局部细节方面有天然优势。

3.1 网格处理

由于本文方法得到的网格会出现有两个边都在叶片边缘的三角形，首先要对这种三角片进行处理。处理流程如下：

1）建立每个顶点的信息索引，包括顶点与相邻点的索引关系，以及与所在面的索引关系；

2）遍历顶点信息，如果顶点只在一个三角形中，则该三角形为待处理的三角形，该顶点为孤立点；

3）分割待处理的三角形；

4）更新顶点信息索引。

分割待处理的三角形的方法如图4所示。其中图4(a)为要处理的三角形在网格中的拓扑示意图，虚线为叶片的轮廓边。对图4(a)情况进行处理，如图4(b)所示，取BC中点E，然后连接AE、DE。

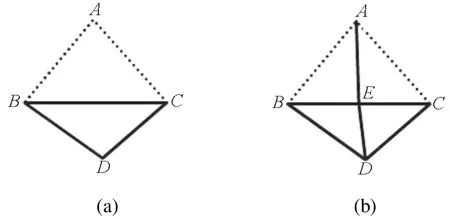
图4 网格处理

3.2 拉普拉斯坐标

设v1, v2,…vn为网格上的顶点位置，i'表示与vi相邻的顶点索引集，则顶点vi的拉普拉斯坐标用如下式计算

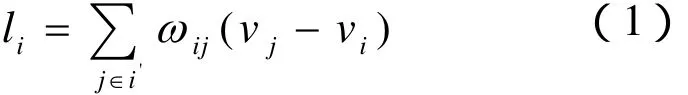
其中，ωij表示vi与vj所在边相对于vi的权重，本文取ωij= c otαij+ c ot βij。这样表示的拉普拉斯坐标可以看作为vi点的平均法向曲率的近似值。任意点的拉普拉斯坐标可以看作是其相邻点集合的权重平均，所以它在一定程度上表达了该点的局部几何信息。拉普拉斯坐标的计算公式表达成矩阵形式如下

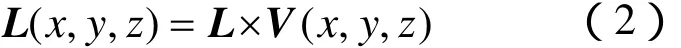
其中， L ( x, y, z)为 n×3阶拉普拉斯坐标矩阵，V (x, y, z)为n×3阶顶点坐标矩阵，L为n×n阶拉普拉斯系数矩阵，L中的对角线元素为非对角线元素为-ωij(i，j=1,2…n)，当 vi、vj不相邻时， -ωij为 0。L 矩阵的秩为n-1，且在变形中该矩阵保持不变。

3.3 拉普拉斯变形系统

构造一个误差函数，用来表达变形前后几何信息的差异，误差函数可以用下式表示

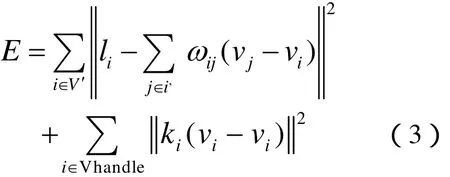
ui为操作点的坐标，Vhandle 表示操作点的集合，ki为调控参数。我们的目的是找到最合适的点，使得上式最小。解这一问题最后可以归结为解超定稀疏线性方程组的问题

V(x, y, z)为待求的未知顶点坐标矩阵，H为操作点系数矩阵，该矩阵元素hii=1，当且仅当vi点为操作点，其余元素都为0。h(x, y, z)为操作点变形之后的坐标与ki的乘积矩阵。每次操作控制点进行变形时，都更新b，之后解线性方程组得到变形之后的点坐标。本文利用稀疏矩阵的Cholesky分解法解该方程组。

4 实验结果与讨论

上述系统在VC2005和OpenGL图形引擎编程环境下实现，并在配置为1.96G HZ的CPU ,DDR 2G内存以及ATI RHD2400显卡的PC机上进行实验。图5为一个黄瓜叶片曲面网格形成过程：图5(a)为初始输入的轮廓以及中轴点（由扫描仪获得），图 5(b)为由样条插值生成的轮廓中轴曲线，图5(c)为生成的初始网格，图5(d)在图5(c)的基础上进行了一次细分，图 5(e)消除了有两条边在轮廓上的三角形，红色线框指出了经过处理的网格。图6为叶片的变形过程：图6(a)为未变形时的叶片曲面，图6(b)为用鼠标选取操作点的过程，红色的点为操作点，图6(c)、(d)、(e)为经过变形之后的叶片曲面，其中由蓝色圆框圈中的点为在变形过程中拖动的操作点。该叶片曲面网格包含 2600个点，每次变形计算用时 219毫秒，能够满足实时性交互速度。

利用本文方法可以较容易地生成叶片在自然情况下发生的变形现象。图7为利用本文方法对黄瓜叶片萎蔫的模拟：其中图7(a)为现实中黄瓜叶片萎蔫的形态，图7(b)为生成的黄瓜叶片曲面，图7(c)和图7(d)为对图7(b)进行变形操作后得到的叶片萎蔫模拟效果。图8为对西瓜叶片自然状态下的模拟：图8(b)为西瓜叶片曲面，图8(c)和图8(d)为变形之后得到的西瓜叶片在自然状态下的形态模拟。

叶面积是农业生产上的重要指标，利用叶面积可以计算作物冠层光分布，从而估算植物的光合作用强度[13]。本文对系统生成的叶片面积与实际的叶片面积进行了比较。分析利用实测数据作为轮廓中轴输入生成的叶面积误差，其中输入的左右边缘点各为22个，中轴点为5个。实际叶片的面积利用三维扫描仪得到的结果来计算，而对于系统生成曲面的面积通过累加所有三角面片面积来获得，且每个三角形的面积用海伦公式计算。计算结果如表2所示，我们取出误差最大的5组数据，可以看出误差都限制在8%之内。对于根据叶脉形态方法生成的叶片面积，也用上述方法计算误差。取生长期的叶片作为测试，得到的误差在14%左右。

用实测数据作为系统输入得出的叶片在叶面积上与实际相差较小，可以为光分布计算打下良好基础，但是需要通过对实际叶片进行扫描，前期工作量相对第二种方法要大；对于利用叶脉形态作为系统输入的方法，其中的参数是根据一定量的数据进行统计学分析得到的，可以反映各个时期叶片的总体形态特征，但是会有一定误差，误差基本在14%以内。但是利用该方法可以只通过输入主脉长度就可以迅速构建出叶片曲面，而不需要对每个叶片进行三维数字化，如果需要迅速构建叶片形态，利用这种方法最方便。

图5 叶片曲面生成过程

图6 叶片变形过程

图7 黄瓜叶片萎蔫模拟

图8 自然状态的西瓜叶片模拟

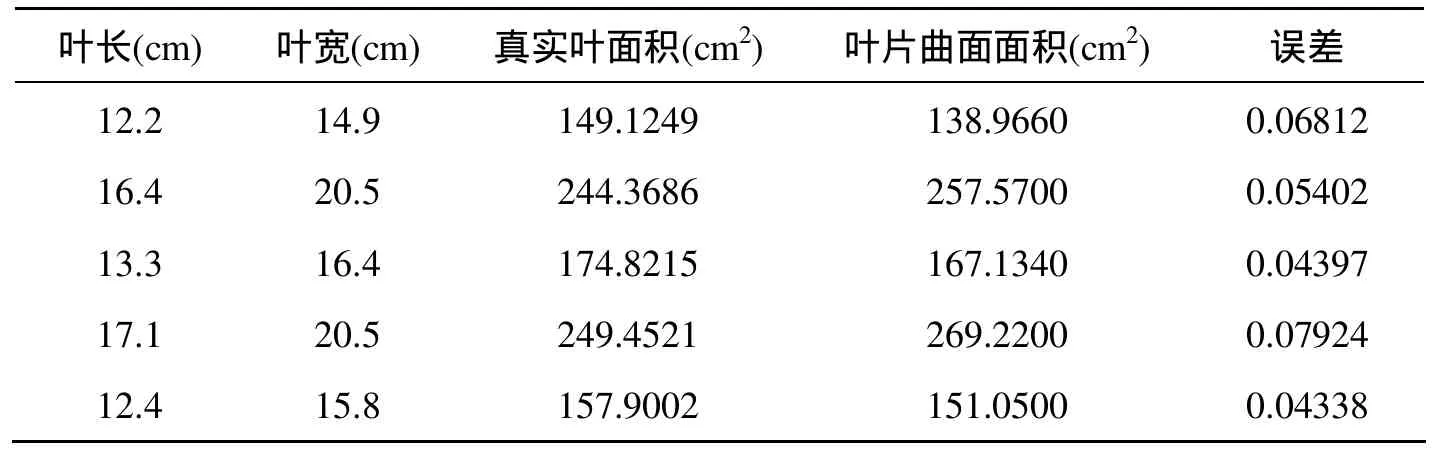
表2 生成叶片曲面面积与真实叶片面积的比较结果

5 结 论

本文介绍了一种新的三维植物叶片设计方法，通过拉普拉斯网格变形技术对叶片的曲面网格进行交互式编辑，利用本方法生成的叶片不仅在形态上具有较强的真实感，同时能够很好地保持叶片的面积特征。需要说明的是，本文的方法不一定要以叶片轮廓及中轴点数据作为输入生成网格曲面，也可以直接在已有的网格曲面上进行变形操作，能够应用于所有的植物叶片，因此具有较好的普适性。

本文的系统在渲染流程中只应用了简单的纹理以及基本的光照，并没有考虑散射光以及叶片材质特性对渲染结果的影响。在今后的工作中，将加入对该部分的模拟，以求得到更真实的效果。

[1]Rozenberg G ,Lindenmayer A. Developmental systems with locally catenative formulas [J]. Acta Informatica,1973, 2(3): 214-248.

[2]Rodkaew Y, Lursinsap C, Fujimoto, et al. Modeling leaf shapes using L-systems and genetic algorithms [C]//Proceedings of NICOGRAPH2002, Tokyo, Japan,2002: 73-78.

[3]Mündermann L, MacMurchy P, Pivovarov J, et al.Modeling lobed leaves[C]//Proceedings of Computer Graphics International, Tokyo, Japan, 2003: 60-65.

[4]Lu S L, Guo X Y, Zhao C J, et al. Modeling of organs and structures generating for crops [C]// International Symposium on Crop Modeling and Decision Support,Nanjing, China, April, 2008: 669-673.

[5]Loch B, Belward J, Hanan J. Application of surface fitting techniques for the representation of leaf surfaces [C]//Zerger A, Argent R M(eds). International Congress on Modelling and Simulation, Melbourne: MODSIM Press, 2005: 1272-1278.

[6]Rodkaew Y, Siripant S, Lursinsap C, et al. An algorithm for generating vein images for realistic modeling of a leaf [C]//Proceedings of Computational Mathematics and Modeling (CMM2002), Bangkok,Thailand, 2002: 223-228 .

[7]Runions A, Fuhrer M, Lane B, et al. Modeling and visualization of leaf venation patterns [J]. ACM Transactions on Graphics, 2005, 24(3): 702-711.

[8]Wang L F, Wang W L, Dorsey J, et al. Real-time rendering of plant leaves [J]. ACM Transactions on Graphics, 2005, 24(3): 712-719.

[9]Baranoski G V G, Rokne J G. Efficiently simulating scattering of light by leaves [J]. The Visual Computer,2001, 17(8): 491-505.

[10]Sung M H, Simpson B, Gladimir V G B. Interactive venation-based leaf shape modeling [J]. Computer Animation and Virtual Worlds, 2005, 16(3-4):415-427.

[11]Cignoni P, Montani C, Scopigno R, et al. A fast divide and conquer delaunay triangulation algorithm in ed [J]. CAD, 1998, 30(5): 333-341.

[12]陆声链, 郭新宇, 李长锋. 三维植物叶片精确建模和绘制技术研究[J]. 中国图象图形学报, 2009,14(4): 731-737.

[13]温维亮, 孟 军, 郭新宇, 等. 基于辐射照度的作物冠层光分布计算系统设计[J]. 农业机械学报,2009, 40: 190-193.