基于神经网络的舰船运动模型辨识
2012-07-07李春风白舒毓林
李春风白舒毓林 龙
1中国人民解放军91388部队91分队,广东湛江524022
2东北林业大学机电工程学院,黑龙江哈尔滨150040
基于神经网络的舰船运动模型辨识
李春风1白舒毓2林 龙1
1中国人民解放军91388部队91分队,广东湛江524022
2东北林业大学机电工程学院,黑龙江哈尔滨150040
通过神经网络对线性水动力系数、弱非线性水动力系数和强非线性水动力系数进行了研究,利用免疫模糊遗传算法对各神经网络辨识器进行优化,以确定舰船运动的待识别系数,并且进行了10°/10°Z形操舵运动、30°回转操舵运动和35°回转操舵运动辨识的仿真。结果表明:利用辨识所得的各种典型操舵运动曲线与利用原参数所得结果符合良好。
舰船运动模型;神经网络;辨识;非线性
0 引 言
在舰船运动控制领域通常要建立舰船的数学模型,一是建立舰船操纵模拟器(Naval Vessel Ma⁃neuverability Simulator),为研究闭环系统性能提供一个基本的仿真平台;二是直接为设计舰船运动控制器服务[1]。对于大型舰船运动及控制问题而言,可以忽略起伏运动、纵摇运动及横摇运动,而只需讨论前进运动、横荡运动和艏摇运动的三自由度平面运动,对于航迹跟踪、航向保持等具有足够的精度。数学模型的建立首先要获得众多的水动力系数。
目前,在舰船设计阶段确定水动力系数的方法主要有4种:基于约束船模试验的方法;利用经验公式或数据库估算的方法[2];理论或数值计算方法;自由自航船模试验加系统辨识的方法。自由自航船模试验加系统辨识的方法把舰船视为一个非线性动态系统,通过自由自航船模试验,测得系统输入(舵角、螺旋桨转速等)和系统输出(船速、艏向角、船模位置等),再利用系统辨识方法得到舰船操纵运动方程中的水动力导数。这种方法简单有效,可直接用于实船试验结果的分析,从而避免由船模和实船雷诺数不同带来的“尺度效应”。
本文在以上研究的基础上,对模型中众多的水动力系数进行了划分,以确定不同舰船运动对应的待辨识的系数。利用线性网络、非线性网络、多元线性回归及对模型进行适当变形的方法对模型中的线性系数、弱非线性系数、强非线性系数进行了有效辨识。
1 舰船水动力系数划分
舰船在小舵角操舵时,运动常以线性力和力矩为主,而在大舵角操舵时,线性力虽然重要,但非线性力作用却相当大。这一点在敏感性分析和运动模拟中,可以明显体现出来,所以辨识可按下列步骤进行[3-5]:
1)选取一组参数初始值进行运动模拟;
2)利用小舵角运动辨识线性水动力系数,此时非线性水动力系数取模拟运动时的值;
3)利用大舵角运动来辨识非线性水动力系数,此时线性水动力系数取其辨识后的值。这个过程应经过多次重复,直到各系数的变化达到很小以及模拟结果达到相当的精度为止。
但是,线性项和非线性项的个数仍然很多,必须仔细分析输入数据与参数之间的关系,敏感性分析为此提供了很好的线索,以确定哪些运动的数据对哪些参数的贡献大[6]。
由于参数可辨识性问题,惯性力导数项可通过模型试验或通过理论计算得到。在这里仅考虑水动力系数。舰船水动力系数辨识过程如图1所示。通过对同一速度的各种运动分析[7],按非线性程度,可以认为辨识中的线性项,如 Xuu,Yv,Yr,Nv,Nr等对应于小角度运动,如10°/10°Z形操舵运动。非线性项分为弱非线性项和强非线性项,其中弱非线性项,如 Xvv,Xvr,Xrr,Yv||v,Yr||r,Nv||v,Nr||r等对应于30°回转操舵运动,强非线性项,如Yvvr,Yvrr,Nvvr,Nvrr等对应于35°回转操舵运动。

图1 舰船水动力系数辨识过程Fig.1 Identification process of naval vessel hydrodynamic coefficients
2 免疫遗传神经网络辨识舰船水动力系数
根据以上分析,可以针对微分方程中的线性项、弱非线性项及强非线性项分3个步骤进行辨识,下面分别详述。
2.1 利用神经网络辨识线性水动力系数
1)在图1所示的水动力系数辨识过程中,第一个微分方程的线性项为Xuu。因为涉及到平方项,以下单独考虑。现仅考虑第2个和第3个微分方程,此时,两个微分方程中除线性项以外其它各项系数均视为已知,则可作如下转换:

将两个微分方程化为式(1):

将上式中的微分v̇和ṙ在时间t上差分,得到:

式中,X(k)和X(k+1)分别为k时刻和k+1时刻的向量为k时刻的。如此,可将估算水动力导数的问题转化为求系数矩阵A(B为已知),使得式(1)成立。由此可以看出,有可能应用递推方法进行求解。
线性神经网络是最简单的一种神经网络,它由一个或多个线性神经元构成。线性神经网络是采用基于最小二乘法(LMS)的Widrow-Hoff学习规则来调节网络权值和阈值,其模型结构为:

其中Out表示输出,In表示输入,purelin()表示网络输出函数,式(3)表达的是输入与输出之间的线性关系。W为系数矩阵。试将式(3)与式(1)比较,可以看出它们具有相同的形式。因此,根据一系列的δ(k)和 X(k)值,就可以训练网络,从而辩识出系数矩阵A。网络结构图如图2所示。实际训练过程中,首先根据k时刻的u(k),v(k),r(k)计算出A′和C′,B′和D′为已知,根据神经网络计算出v(k+1),r(k+1)并与实际值相比较,它们之间的差值即作为网络训练的误差函数。

图2 线性神经网络结构图Fig.2 The chart of linear neural network
2)这里 Xuu并不采取某种方法将其单独辨识出来,而是令H(u2)=Xuuu2,利用神经网络辨识函数H(u2),其它系数取其辨识后的值或初始值。网络结构如图3所示,采用遗传算法优化网络权值,每一时刻将网络输出H(u2)代入到微分方程组中,解出u值并与网络输入u相比较,其差值即作为网络训练的目标函数。最后,网络训练结束后,再利用多项式线性回归方法求取系数Xuu。
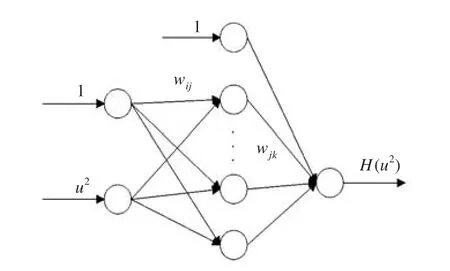
图3 Xuu辨识网络结构图Fig.3 The chart ofXuuidentification network
2.2 利用神经网络辨识弱非线性水动力系数
1)Xvv,Xvr,Xrr的辨识
Xvv,Xvr,Xrr的辨识过程与 Xuu类似。令H(vv,vr,rr)=Xvvv2+Xvrvr+Xrrr2,其它过程同第2.1节的第2)部分,这里不再赘述。网络结构图如图4所示。

图4 Xvv,Xvr,Xrr辨识网络结构图Fig.4 The chart ofXvv,Xvr,Xrridentification network
2)Yv||v,Yr||r,Nv||v,Nr||r的辨识
Yv||v,Yr||r及 Nv||v,Nr||r的辨识方法同上,其中 HY(vv,rr)=Yv||vv ||v+Yr||rr ||r , HN(vv,rr)= Nv||vv ||v+Nr||rr ||r,HY(vv,rr)的辨识网络结构图如图5所示,HN(vv,rr)的辨识网络结构图与此相似,只是将输出换成HN(vv,rr)。

图5 Yv||v,Yr||r,Nv||v,Nr||r辨识网络结构图Fig.5 The chart ofYv||v,Yr||r,Nv||v,Nr||ridentification network
2.3 利用神经网络辨识强非线性水动力系数
令 HY(vvr,vrr)=Yvvrv2r+Yvrrvr2,HN(vvr,vrr)=Nvvrv2r+Nvrrvr2,其辨识方法与上类似。网络结构图如图6所示。
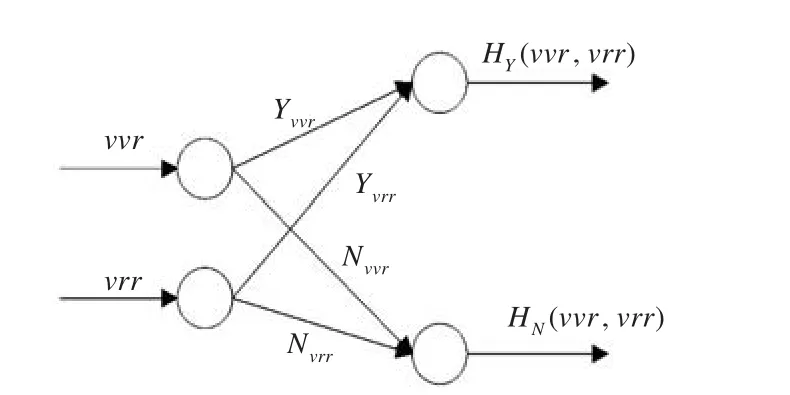
图6 Yvvr,Yvrr,Nvvr,Nvrr辨识网络结构图Fig.6 The chart ofYvvr,Yvrr,Nvvr,Nvrridentification network
2.4 利用免疫模糊遗传算法优化辨识网络
本节利用免疫模糊遗传算法对上述神经网络辨识器进行优化,采用实数编码方法对每个网络中的权值编码[8-10]。针对图2中线性神经网络的辨识过程如图7所示,可编码如下:α1α2α3α4。

免疫模糊遗传算法(IFGA)初始化时,可采用随机初始化方法。算法使用算术交叉。误差函数:
适应度函数:

式中,v̂(k+1),r̂(k+1)为被辨识系统输出;v(k+1),r(k+1)为网络输出;q为用于网络训练的输入输出采样数据对的个数;为了避免出现除零情况发生,将δm设为一个正的小量(如0.001)。种群规模N=50,遗传进化1 500代。

图7 Y′v,Y′r,N′v,N′r辨识过程Fig.7 Identification process ofY′v,Y′r,N′v,N′r
其它系数的辨识及用免疫模糊遗传算法的优化设计与此类似。
3 仿真验证
如前所述,利用10°/10°Z形操舵运动所获得的数据来辨识 Xuu,Yv,Yr,Nv,Nr等线性系数。图8为训练结束后,利用辨识系数所得的10°/ 10°Z形操舵运动曲线,及与原参数所得曲线的对照结果。
利用30°回转操舵运动所获得数据来辨识Xvv,Xvr,Xrr,Yv||v,Yr||r,Nv||v,Nr||r,aH等弱非线性系数。图9为训练结束后,利用辨识系数所得的30°回转操舵运动曲线,及与原参数所得曲线的对照结果。


图8 10°/10°Z形操舵运动原参数结果与辨识参数结果比较(ψ,δ,r,v,u)Fig.8 Comparison between identification parameters and original parameters of 10°/10°Z shape steering movement(ψ,δ,r,v,u)
利用35°回转操舵运动所获得数据来辨识Xvv,Xvr,Xrr,Yv||v,Yr||r,Nv||v,Nr||r,aH等弱非线性系数。图10为训练结束后,利用辨识系数所得的35°回转操舵运动曲线,及与原参数所得曲线的对照结果。分别给出了航向角、舵角、艏摇角速度、横荡速度、前进速度曲线,回转操舵运动还给出了Y-X曲线,其中“—”为原参数结果,“…”为辨识参数结果。


图9 30°回转操舵运动运动原参数结果与辨识参数结果比较(Y-X,ψ,δ,r,v,u)Fig.9 Comparison between identification parameters and original parameters of 30°rotation steering movement(Y-X,ψ,δ,r,v,u)
从各图中的曲线对比,可以看出,本文所提的辨识方法是行之有效的,利用辨识参数所得的各种典型操舵运动曲线与利用原参数所得结果符合良好。


图10 35°回转操舵运动原参数结果与辨识参数结果比较(Y-X,ψ,δ,r,v,u)Fig.10 Comparison between identification parameters and original parameters of 35°rotation steering movement(Y-X,ψ,δ,r,v,u)
表1~表3分别给出线性系数、弱非线性系数和强非线性系数的原有值与辨识结果的对比。

表1 原参数与辨识参数结果比较(线性系数)Tab.1 Comparison between identification parameters and original parameters(linearity coefficients)

表2 原参数与辨识参数结果比较(弱非线性系数)Tab.2 Comparison between identification parameters and original parameters(infirmness nonlinear coefficients)
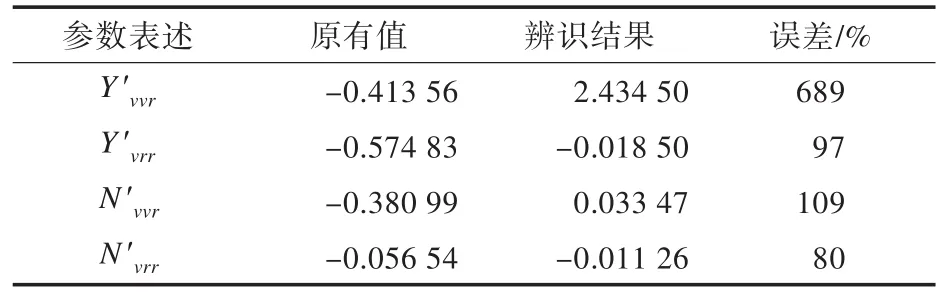
表3 原参数与辨识参数结果比较(强非线性系数)Tab.3 Comparison between identification parameters and original parameters(strong nonlinear coefficients)
由表1可以看出,辨识结果与原系数的误差不大于4.05%,而由表2和表3可见,辨识结果与原系数的误差要大得多,这是由于多元线性回归方法只是使模型与待拟合对象间的误差达到最小,但没能很好地控制模型中参数值的分配,导致某些参数比实际值大或小。虽然如此,本方法对于舰船模型的整体及线性参数的辨识精度仍可以达到要求。
4 结 论
本文将免疫遗传神经网络和多元线性回归方法结合起来对舰船前进、横荡、艏摇三自由非线性耦合模型的水动力系数进行辨识。将大量的待辨识系数分为线性系数、弱非线性系数、强非线性系数,并且分别利用10°/10°Z形操舵运动、30°回转操舵运动和35°回转操舵运动来对其进行辨识,这样既可以提高系数辨识的精度,又可以使每次待辨识的系数数量较小,运算速度更快。将可转化为统一形式的横荡、艏摇两个方程中的4个线性水动力系数采用免疫遗传线性神经网络进行辨识,而其它在同一方程中对应于同一操舵运动的各项系数分别采用免疫遗传非线性神经网络来辨识其在方程中所对应的各项水动力(矩)值的总和,待免疫遗传非线性神经网络辨识结束后,再采用多元线性回归方法辨识所包含的水动力系数。虽然经多元线性回归方法辨识所得的水动力系数与其原有值差距较大,但本文方法可以获得精确的线性水动力系数及整体模型,这对于模型复杂,水动力系数难辨识的问题不失为一种有效的解决方法。
[1] 唐晓光,刘祖源.基于神经网络的船舶操纵运动水动力预报[J].武汉理工大学学报:交通科学与工程版,2002,26(1):25-27.
TANG X G,LIU Z Y.Hydrodynamics prediction of ship maneuverability using neural network[J].Journal of Wuhan University of Technology(Transportation Science and Engineering),2002,26(1):25-27.
[2] MAHFOUZ A B,HADDARA M R.Effect of the damp⁃ing and excitation on the identification of the hydrody⁃namic parameters for an underwater robotic vehicle[J]. Ocean Engineering,2003,30(8):1005-1025.
[3] 张晓兔,张乐文,刘祖源.基于RBF网络的操纵水动力预报[J].武汉交通科技大学学报,1999,23(6):602-604.
ZHANG X T,ZHANG L W,LIU Z Y.Prediction of ship maneuverability hydrodynamics based on Radial Basis Function neural network[J].Journal of Wuhan Transportation University,1999,23(6):602-604.
[4] 刘清,吴秀恒,邹早建,等.基于双级模糊控制器的船舶操纵运动控制系统[J].武汉交通科技大学学报,2000,24(3):229-232.
LIU Q,WU X H,ZOU Z J,et al.Ship maneuvering control system based on two-stages fuzzy controller[J].Journal of WuhanTransportation University,2000,24(3):229-232.
[5] 吴松,李华.人工神经网络在舰船火灾探测中的应用[J].中国舰船研究,2007,2(6):55-58.
WU S,LI H.Application of artificial neural network in the fire detection of naval vessel[J].Chinese Journal of Ship Research,2007,2(6):55-58.
[6] 张桂臣,任光.基于航迹误差预测模型的船舶自适应控制[J].大连海事大学学报:自然科学版,2007,33(4):37-41.
ZHANG G C,REN G.Ship self-adaptive control based on predicting tracking error model[J].Journal of Da⁃lian Maritime University,2007,33(4):37-41.
[7] 张金梅.基于模糊推理的智能控制系统的现状和展望[J].科技情报开发与经济,2004,14(1):126-128.
ZHANG J M.Present situation and prospect of the in⁃telligent control system based on the fuzzy reasoning[J].Sci-Tech Information Development and Economy,2004,14(1):126-128.
[8] 梁鸿生,郝勇娜,王凯,等.免疫算法[J].昆明理工大学学报:理工版,2003,28(5):1-5.
LIANG H S,HAO Y N,WANG K,et al.Immune al⁃gorithm[J].Journal of Kunming University of Science and Technology(Science and Technology),2003,28(5):1-5.
[9] 刘东东,陈兵,王华明.基于卷积型小波包变换的船用水位调节器故障辨识[J].中国舰船研究,2010,5(1):68-71.
LIU D D,CHEN B,WANG H M.Fault recognition of water level regulator based on the convolution type of wavelet packet[J].Chinese Journal of Ship Research,2010,5(1):68-71.
[10] 张志刚.人工神经网络的混合电力补偿控制器设计[J].电机与控制学报,2008,12(3):353-356,360.
ZHANG Z G.Design of controller based on neural net⁃works in hybrid power compensation[J].Electric Ma⁃chines and Control,2008,12(3):353-356,360.
[责任编辑:喻 菁]
Identification of Naval Vessel Movement Model Based on Neural Network
LI Chun-feng1BAI Shu-yu2LIN Long1
1 The 91388th Unit of PLA,Zhanjiang 524022,China
2 Electrical and Mechanical Engineering College,Northeast Forestry University,Harbin 150040,China
On the basis of neural network theory,this paper investigated the hydrodynamic coefficients of the linear type,weakly nonlinear type and strongly nonlinear type.To determine the coefficients of vessel movement,all neural network identifiers were optimized through the fuzzy immune genetic algorithm.Al⁃so,simulations on wheel movements for the 10°/10°Z shape,30°circumgyratetion and 35°circumgyrate⁃tion were performed.The results show that the corresponding curve for each wheel movement agrees well with the input parameters,which validates the effectiveness of the proposed approach.
naval vessel movement model;Neural Network;identification;nonlinear
U661.3
A
1673-3185(2012)05-60-06
10.3969/j.issn.1673-3185.2012.05.011
2012-03-13
李春风(1983-),男,硕士,助理工程师。研究方向:船舶先进控制理论的研究。
E⁃mail:chunfeng_19830401@163.com
李春风。
