变周期减摇水舱控制与仿真

孙宝国 谢广东

中国舰船研究设计中心，上海201102

变周期减摇水舱控制与仿真

孙宝国 谢广东

中国舰船研究设计中心，上海201102

减摇水舱的设计首先要考虑与船体的适配，同时在设计中要重点考虑水舱的阻尼与周期特性，其中周期特性是水舱最基本的特性参数，适用周期范围越宽，减摇效果越理想。针对变周期减摇水舱的相当长度与一般U型水舱相当长度计算的不同之处——其连通道宽度可调且边舱面积随边舱外壁角变化而变化，通过积分方法推导出了可变周期减摇水舱相当长度的计算公式，提出了一种适用于变周期减摇水舱的估算方法。所设计的变周期减摇水舱采用连通道挡板控制改变周期，避免了气阀控制的时间延迟问题，还可根据船体运动规律调整连通道阻尼挡板以提高减摇效果。以某型船为例，建立了船舶减摇水舱仿真模型。经减摇水舱自由衰减振荡数值仿真方法验证，所提出的周期估算公式可靠。采用该模型研究了变周期减摇水舱的控制方法，结果表明，在其工作范围内，可使横摇角始终保持在8°以内，可以在5.5～18 s的周期范围内有效减摇，大大超过了被动式减摇水舱的工作频带。

变周期减摇水舱；固有周期；自由振荡；减摇效果

0 引 言

减摇水舱是目前船舶最常用的减摇装置之一，依靠横摇运动所产生的能量使水舱内的水流动，从而产生减摇力矩以减少船舶的横摇。它具有结构简单，造价低廉，便于维护与保养等优点，目前普遍应用于RORO船、科学考察船、运输船等。

减摇水舱依据控制方式可分为被动式减摇水舱、可控被动式减摇水舱和主动式减摇水舱。被动式减摇水舱由于结构形式固定，减摇频带较窄，减摇能力相对较差；主动式减摇水舱由于消耗能量较多，目前应用很少；可控被动式减摇水舱通过一定的控制，拓宽了减摇的频带，同时耗能极小，因此被广泛应用。国际上，可控被动式减摇水舱主要有两种形式，一种是INTERING气阀式可控被动式水舱，采用气阀开关控制空气连通道，延长水舱的固有周期；另一种为JFE和Stabilio的可变周期减摇水舱，通过挡板控制水连通道的连通面积，拓展减摇周期的范围，通过控制不同位置和数量的挡板开关来调节减摇水舱的工作状态，使其适应不同的航行环境，达到最佳的减摇效果［1-2］。

本文通过建立“船舶—减摇水舱”数学仿真模型，首先利用计算流体力学的方法，计算不同状态下减摇水舱的固有周期，然后根据船舶的运动规律设计控制策略，基于某船完成变周期减摇水舱减摇效果计算，进行减摇能力分析。

1 数学模型

1.1 海浪仿真模型

海浪运动属于随机过程，多以功率谱的形式表示频率特性。至今所提出的大多数谱都具有如下结构形式：

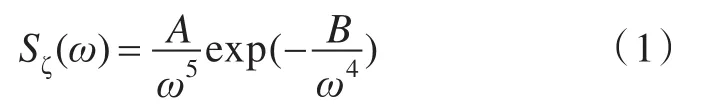
式中，A及B中包含风要素（风速、风时、风距）或波要素（波高、周期）。文中仿真采用P-M谱，式中，g为重力加速度，H1/3为有义波高。

海浪对船舶的横摇干扰力矩主要与波倾角有关，在研究船舶的横摇运动及控制系统时，需要考虑海浪波倾角αe对船舶及其控制系统的影响，海浪波倾角可视为零均值的平稳随机过程。

波倾角谱和波高频谱的关系为：

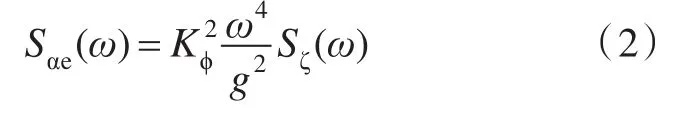
式中，Kϕ为有效波倾系数。

当船以一定航速和浪向航行时，波浪实际作用于船体上的频率已不同于自然频率，而表现为遭遇频率ωe。根据能量等效原则，遭遇频率能量谱密度与自然频率能量谱密度函数之间有如下关系：

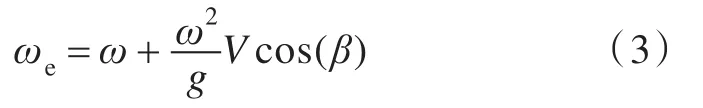
式中，V为航速，kn；β为遭遇角，（°）。

根据能量守恒，波倾角遭遇谱如下所示：

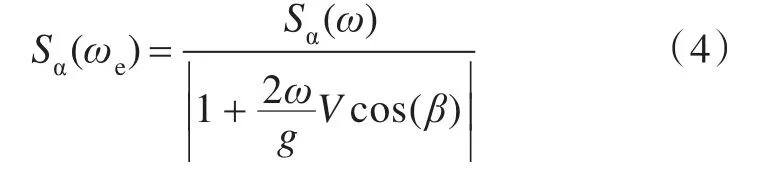
时域内的波倾角可以通过线性叠加法，采用下式进行仿真：

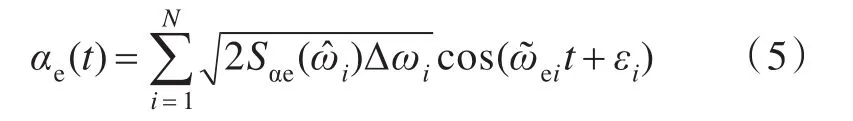
1.2 船舶水舱系统数学模型

船舶横摇运动数学模型为：

式中，φ为船舶横摇角，（°）；I1+Jt为船舶自身的质量和附加质量对x轴的惯性矩，（t·m2）；D为船舶的排水量，t；为初稳心高，m；c为边舱轴线到船舶纵中剖面的距离，m；2Nφ为船舶的横摇阻尼力矩比例系数；S0为单边舱的自由液面面积，m2；z值表示水舱右边舱中的液位向上移动的位移，m；b2为水舱轴线对于船舶横摇轴的静矩，具有面积因次，可以表示为：式（6）中Jt可以表示为：

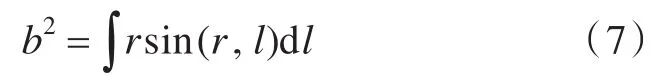
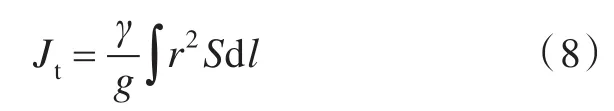
水舱内液体振荡的微分方程式为：

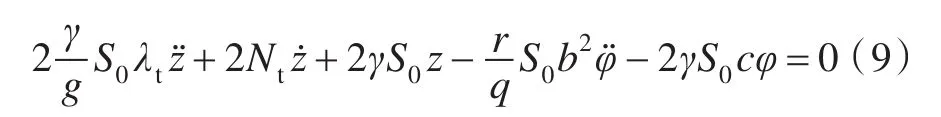
式中，2Nt为减摇水舱的横摇阻尼力矩比例系数；为水舱内水柱的相当长度，m。

考虑到船舶在不规则波中的横摇情况，减摇装置的效果可以用减摇前和减摇后的三一横摇幅值的比值来表示［3-4］，称为减摇比K，即

式中，m0为横摇能谱的0次矩；m2为横摇能谱的2次矩；m4为横摇能谱的4次矩。

2 可变周期减摇水舱工作原理

可变周期减摇水舱基本结构如图1所示。水舱边舱用挡板隔开，分成Tank A和Tank B两个部分，对应设置两个空气连通道，用两个阀F1和F2控制其开关。在底部连通道设置3个旋转挡板D1，D2和D3。

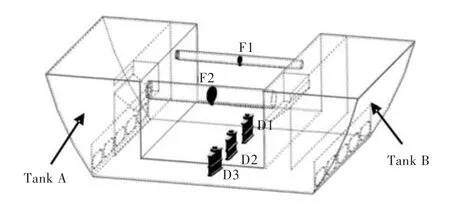
图1 可变周期减摇水舱实物简图Fig.1 Physical diagram of variable-cycle anti-rolling tanks

当船舶横摇频率超出水舱的工作范围时，水舱减摇效果不理想，甚至会出现增摇，为船舶的安全性带来不利影响，需要通过气阀F1和F2关闭减摇水舱。当船舶横摇频率在水舱的工作范围内时，可以通过控制F1和F2两个气阀对A，B舱进行切换。进一步通过对水舱挡板D1，D2和D3的转动进行连续控制，改变水舱的固有周期。挡板叶片可以在0°～90°内任意角度旋转，根据船舶的横摇角、横摇角速度等信息以及水舱内液体的流动状态预测系统运动参数的变化，以此为反馈控制信号，利用叶片的角度调整水舱内液体振荡参数，使液体的流动适应船舶横摇周期的变化，达到有效减摇的目的［5］。

可变周期减摇水舱可以工作在表1所示的不同状态下。

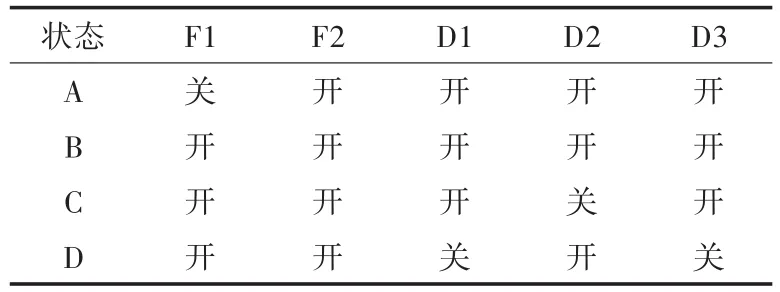
表1 可变周期减摇水舱的4种工作状态Tab.1 Four working states of variable-cycle anti-rolling tanks

3 可变周期减摇水舱周期估算方法

通过变周期减摇水舱的工作原理可知水舱固有周期的计算尤为重要。精确的周期估算对于研究水舱自身的特性，以及水舱的控制都很有必要。

可变周期减摇水舱的周期估算公式为：

式中，g为重力加速度，g=9.81 m/s2。

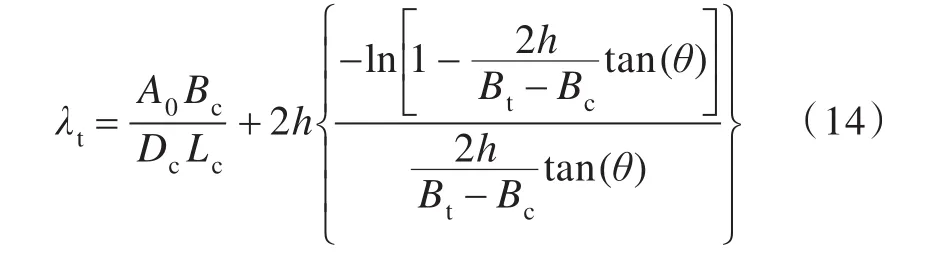
式中，A0为边舱截面积，m2。

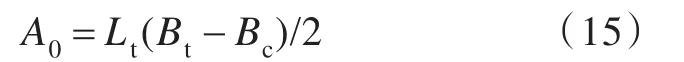
式中，Bc为水舱边舱内壁间距，m；Dc为连通道高度，m；Lc为连通道宽度，m；Lt为两边舱长度，m；Bt为水舱总宽度，m；h为静水面深度，m；θ为边舱倾斜角度，（°）。具体如图2所示。

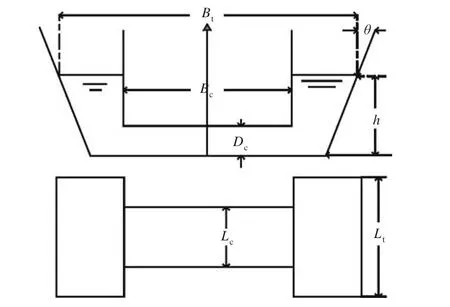
图2 可变周期减摇水舱结构简图Fig.2 Configuration diagram of variable-cycle anti-rolling tank

可变周期减摇水舱周期估算公式中水舱的相当长度不同于一般U型水舱相当长度的计算。其连通道宽度可调，边舱面积随边舱外壁角度的变化而变化。考虑到以上两个方面的不同，通过积分的方法推导出了可变周期减摇水舱相当长度的计算公式。

可变周期减摇水舱也不同于一般气阀控制的减摇水舱，通过水通道挡板控制避免了气阀控制的时间延迟问题，使得控制更加精确、有效。为了便于分析，只考虑水舱工作在B，C，D状态下，把水舱模型简化成只有挡板控制的模型。

为了更加精确地验证水舱的周期特性，采用VOF模型对减摇水舱进行仿真分析。该问题的气液两相流连续方程为［6-7］：

式中，υ为速度矢量，α表示水或空气在单元体中的体积分数，它介于0和1之间。同时满足：

式中，下标w和a分别表示水和空气。

动量方程为：

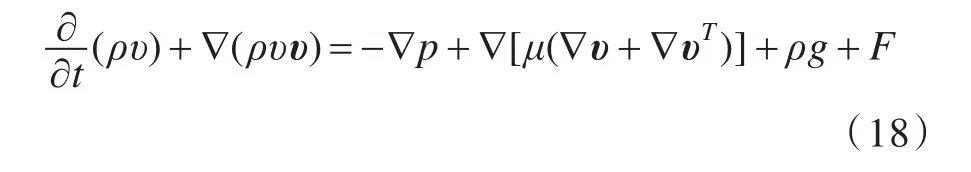
式中，ρ和 μ表示单元的流体密度和动力学粘性系数；p为压力，MPa；g为重力加速度；F为体积力，kN。

ρ由下式确定（μ的确定方法类似）：

4 仿真分析

以某船为例，基本的船型数据如下。

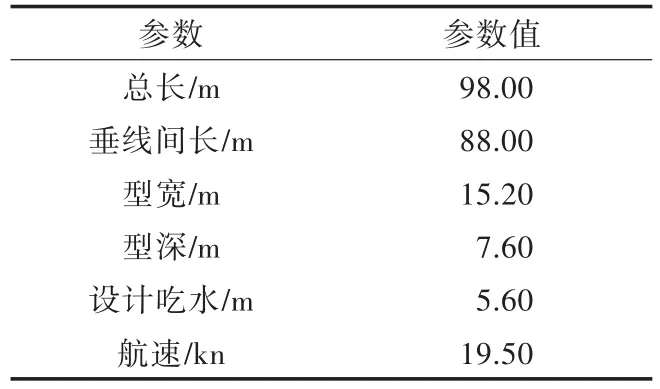
表2 基本的船型数据Tab.2 Basic ship dimensions

根据优化设计方法，设计了水舱的结构以及在船体上的布置，如图3所示。

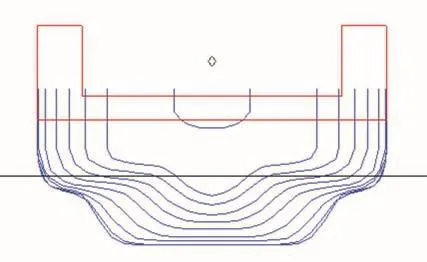
图3 水舱在船体上的布置Fig.3 Configuration of tanks on the ship

4.1 周期仿真验证

本节利用减摇水舱自由衰减振荡数值仿真的方法对水舱的周期计算公式进行验证。分别针对上述3种工作状态下的水舱进行了自由衰减振荡仿真研究，水舱自由振荡初始条件为左边舱液位高度高于右边舱，并通过在边舱内设置波高仪的方法对边舱液位进行实时监控。图4给出了水舱状态C时自由振荡数值仿真气液分布云图。

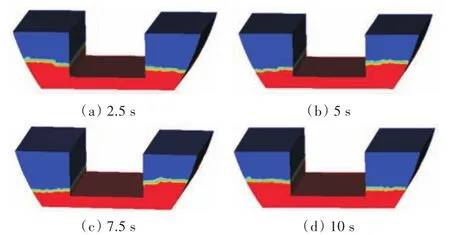
图4 状态C自由振荡过程水舱气液分布云图Fig.4 The gas-liquid contours of tanks in the process of free oscillation at state C

经过仿真计算，可以得出如图5所示的右边舱液位随时间变化曲线图，从而可以计算出水舱周期。经仿真与公式计算得出的水舱周期如表3所示。

图5 右边舱液位随时间变化曲线Fig.5 Time history of the liquid level in right side tank

4.2 减摇效果仿真验证

根据仿真结果，可以得出水舱有效减摇周期范围：状态B，7～11 s；状态C，9～15 s；状态D，11～17 s。

通过监测船舶的横摇角，可以计算出船舶的平均横摇周期。如果平均横摇周期不在减摇系统设计的工作范围内，则水舱关闭；如果平均横摇周期在水舱工作范围内，则根据船舶横摇周期确定水舱的控制方案。每隔一段固定的时间统计一次船舶平均横摇周期，不断选择和调整可变周期减摇水舱的工作状态，使其始终发挥良好的减摇作用。

根据上述方案，建立“船舶—减摇水舱”仿真模型，分别对安装可变周期减摇水舱与被动式减摇水舱的横摇角与横摇减摇效果进行仿真［8-10］，得到的仿真结果曲线如图6和图7所示。

5 结 论

本文研究了变周期减摇水舱的工作原理，推导出了变周期减摇水舱的周期估算公式，并应用数值仿真的方法对这一公式的可靠性进行了验证。从仿真结果可知：

图6 安装可变周期减摇水舱和被动式减摇水舱时的横摇响应对比图Fig.6 The rolling response comparison between variable-cycle anti-rolling tanks and passive anti-rolling tanks

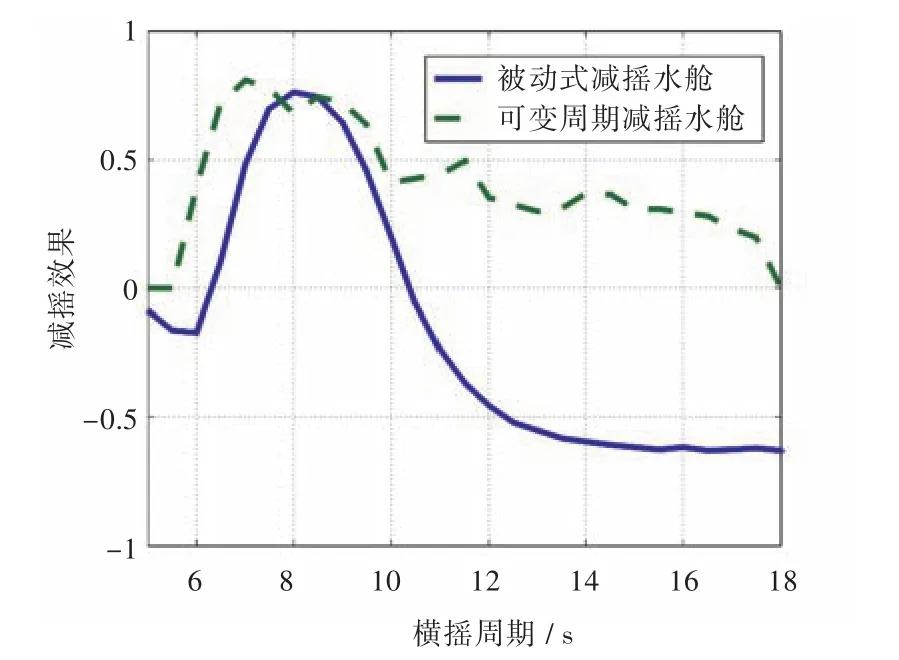
图7 安装可变周期减摇水舱和被动式减摇水舱时的减摇效果对比图Fig.7 Stabilized effect comparison between variable-cycle anti-rolling tanks and passive anti-rolling tanks

1）通过水舱自由振荡仿真计算的结果与周期估算公式计算的结果相差非常小，仅为3.7%左右。因此，利用周期估算公式对水舱的周期进行计算是可行的。

2）从横摇响应上看，可变周期减摇水舱在其工作范围内可使横摇角始终保持在8°以内，具有良好的减摇效果。

3）从减摇范围上看，可变周期减摇水舱可以在5.5～18 s的周期范围内有效减摇，大大超出了被动式减摇水舱的工作频带，而且不产生增摇效果。因此，合理控制的可变周期减摇水舱性能稳定，安全实用。

［1］ STIGTER C.The performance of U-tanks as a passive anti-rolling device［J］.International Shipbuilding Prog⁃ ress，1966，13：249-275.

［2］ MOALEJI R，GREIG A R.On the development of ship anti-roll tanks［J］.Ocean Engineering，2007，34（1）：103-121.

［3］ 贾正余，黄宇，曾启盛，等.可控式被动减摇水舱气道的阻尼［J］.船舶工程，2011，33（3）：41-44.

JIA Z Y，HUANG Y，ZENG Q S，et al.Damping of air duct of passive controlled anti-rolling tanks［J］.Ship Engineering，2011，33（3）：41-44.

［4］ 梁利华，刘志坤，张松涛.减摇水舱的固有频率和阻尼研究与试验分析［J］.船舶工程，2010，32（3）：35-38.

LIANG L H，LIU Z K，ZHANG S T.Study and experi⁃ment analysis on the natural frequency and damping of anti-rolling tank［J］.Ship Engineering，2010，32（3）：35-38.

［5］ PHAIROH T，HANG J K.Adaptive ship roll mitigation by using a U-tube tank［J］.Ocea Engineering，2007，34（3/4）：403-415.

［6］ 张虹，姜德龙，梁利华，等.减摇水舱试验装置研究［J］.机床与液压，2009（12）：77-79.

ZHANG H，JIANG D L，LIANG L H，et al.The re⁃search on test equipment of anti-rolling tank［J］.Ma⁃chine Tool and Hydraulics，2009（12）：77-79.

［7］ 于立君，金鸿章，王辉.减摇水舱半物理仿真装置的试验研究［J］.哈尔滨工程大学学报，2008，29（6）：635-640.

YU L J，JIN H Z，WANG H.Research on experiment of anti-rolling tank semi-physical simulation equipment［J］.Journal of Harbin Engineering University，2008，29（6）：635-640.

［8］ 蒋颉，丁勇.减摇水舱挡板开度对稳定矩影响的研究［J］.中国舰船研究，2011，6（3）：36-39.

JIANG J，DING Y.Stabilizing moment influenced by angle of damping plate of anti-rolling tank［J］.Chinese Journal of Ship Research，2011，6（3）：36-39.

［9］ 杨民.航行状态下减摇水舱减摇能力仿真研究［J］.自动化技术与应用，2008，27（9）：1-5.

YANG M.Simulation study of the efficiency of the an⁃ti-rolling tank［J］.Techniques of Automation and Ap⁃plications，2008，27（9）：1-5.

［10］ 金鸿章，张宏瀚.基于被动式PD控制策略的“双水舱”减摇系统研究［J］.船舶力学，2011，15（10）：1082-1089.

JIN H Z，ZHANG H H.Research on double-tank sta⁃bilizers based on passive PD control strategy［J］.Jour⁃nal of Ship Mechanics，2011，15（10）：1082-1089.

［责任编辑：喻 菁］

Control and Simulation of Variable-Cycle Anti-Rolling Tanks

SUN Bao-guo XIE Guang-dong
Shanghai Division，China Ship Development and Design Center，Shanghai 201102，China

During the design of marine anti-rolling tanks，the suitability of the tank to the ship should be a priority，and the damping and cycle characteristics should be considered at the same time.Particularly，the tank cycle is a fundamental characteristic parameter：the wider range of application it provides，the su⁃perior stabilized effect is obtained.However，the calculation of the considerable length for variable-cycle anti-rolling tanks is distinct from that for general U type tanks，where the width of water channels for vari⁃able-cycle anti-rolling tanks can be adjusted optionally，and the area of side tanks changes along with the outer corner.In view of the problem，this paper proposed a calculation formula for the considerable length of variable-cycle anti-rolling tanks through the integral approach.The target tank adopted water channel baffle control to change the cycle，which avoids time delay caused by the air valve control，and the optimal stabilized effect could be thus realized by adjusting the damping baffle according to ship motion.To vali⁃date the algorithm，a certain ship model was established with free oscillation numerical simulations con⁃ducted.The results show that the roll angle remains within a range of±8°，and the roll stabilization is effec⁃tive with a period range of 5.5 s to 18 s，which significantly exceeds the working band of passive anti-roll⁃ing tanks.

variable-cycle anti-rolling tank；natural period；free oscillation；stabilized effect

U662.2

A

1673－3185（2012）05－22－05

10.3969/j.issn.1673－3185.2012.05.004

2012－02－03

孙宝国（1970－），男，高级工程师。研究方向：舰船总体研究与设计。E⁃mail：sun1bao1guo@163.com

谢广东（1985－），男，硕士，助理工程师。研究方向：舰船总体研究与设计。E⁃mail：xieguangdong0@sina.com

谢广东。