奇异值分解降噪的改进方法

张 磊 彭伟才 原春晖 刘 彦

中国舰船研究设计中心船舶振动噪声重点实验室，湖北武汉 430064

0 引 言

在船舶振动噪声信号的测试过程中，总存在着由现场测试环境及仪器本身产生的误差源［1-4］，其中一个不可避免的误差源就是随机噪声。测量信号中的噪声水平直接决定了分析的可靠性，为此，必须消除或者最小化信号中的噪声干扰。

作为信号降噪的有效方法之一，奇异值分解（SVD）已被广泛应用于许多工程领域，如信号滤波和矩阵秩的估计。将受到噪声污染的信号构造成Hankel矩阵，然后对其进行奇异值分解，将包含信号特征的矩阵分解到一系列奇异值和奇异值矢量对应的子空间中，是对Hankel矩阵进行噪声过滤的一种非线性滤波方法。从SVD降噪的基本原理来看，其关键就是确定Hankel矩阵的有效奇异值数目，奇异值数目选择不当，会极大地影响降噪效果。而目前用于确定奇异值数目的方法，如奇异值曲线、奇异熵增量［5］、信噪比经验［6］等，都不能明确地给出有效阶次，往往只能依靠经验选取。

本文将通过仿真分析与实验测试来研究奇异值数目变化时噪声对信号的干扰影响。

1 奇异值分解降噪基本原理

对于一个受噪声污染的离散信号 X={x1，x2，…，xL}，构造成m×n(m≤n)维的Hankel矩阵为：

式中，A为Hankel矩阵；m为嵌入维数，并且满足m+n-1=L。

对Hankel矩阵进行奇异值分解可得到：

式中，U为m×m维正交矩阵；V为n×n维正交矩阵；Σ为m×n维矩阵。主对角元素为矩阵的奇异值，并且从大到小排列。

矩阵A为由受噪声污染的信号构成的Hankel矩阵，可以表示为未受噪声污染的信号子空间和噪声子空间之和：

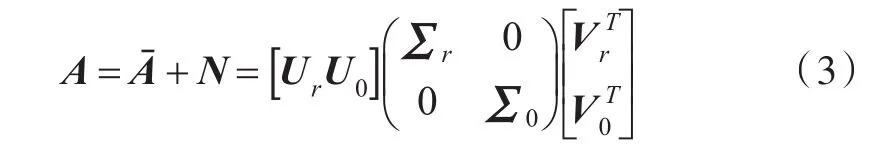
保留对角矩阵的前k个有效奇异值，将其他的奇异值设置为零，利用奇异值分解的逆过程得到重构矩阵。一般来说，这时的重构矩阵不再是Hankel矩阵的形式。为了得到降噪后的信号，需要对重构矩阵中的反对角元素采用下式进行平均：

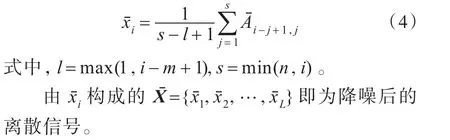
2 改进方法

由实测经验可知，当实际测量环境很好时，测量得到的信号一般为光滑曲线；而当受到外界的随机噪声干扰时，测量得到的信号中就会含有大量的“毛刺”。

利用噪声污染信号构造Hankel矩阵进行奇异值分解降噪，就是对含噪信号进行逼近、剔除毛刺的过程。经过对大量仿真结果的研究，发现去噪结果中剩余噪声对信号的干扰影响能够通过信号中“毛刺”的数量及大小来判断，这与实测经验相吻合。当选取的奇异值数目较小时，大部分噪声都被剔除掉了，但也损失了大量有用信号。随着奇异值数目的逐渐增大，有用信号信息趋于完整，但噪声的干扰也会逐渐增加。当奇异值数目达到某一值时，降噪后的信号既保留了大部分有用信息，也剔除掉了大部分噪声，这就是要选取的最佳奇异值数目。当奇异值数目再增加时，基于随机噪声对信号干扰的特点，降噪后的信号中会出现大量“毛刺”，波动明显，在数学意义上可表示为有大量极值点出现。本文根据降噪后信号极值点（均指极大值点）数量的变化，找到了突变点，可清晰地判断应该选取的有效奇异值数目。

本文信噪比计算所用的公式为：

式中，SNR为信噪比，dB；n(i)为含有噪声的信号；x(i)为真实信号；N为信号长度。

3 仿真分析

3.1 噪声干扰对奇异值的影响

经过对无噪声理想信号和受噪声污染信号的研究，发现一般由无噪声理想信号构造的Hankel矩阵的大部分奇异值为零。根据非零奇异值的数目，可以很容易地判断矩阵的有效阶次。因噪声具有随机和不相关的特点，因此，由受随机噪声污染信号构造的Hankel矩阵呈列满秩或行满秩状态（取决于行和列哪个维数更小）。

现取如图1所示的无噪声理想信号和噪声污染信号进行仿真分析。无噪声理想信号clean signal＝sin（3×t）＋sin（5×t）＋sin（8×t），单位为 V，其中 t为时间间隔为0.01的从0～2变化的时间序列。在无噪声理想信号中加入信噪比约为6dB（通过式（5）计算得到）的高斯白噪声，得到了图1中的噪声污染信号，噪声干扰明显。

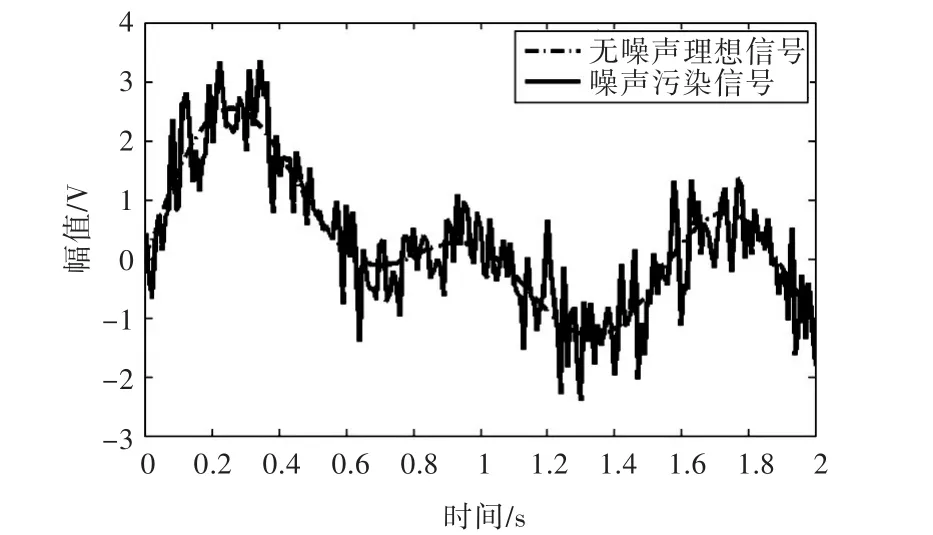
图1 无噪声理想信号与噪声污染信号Fig.1 Clean signal and noisy signal

对图1中的两个信号取维数m＝80，n＝122构造Hankel矩阵（本文在此不讨论如何选取的维数，具体方法可参考文献［8］），进行奇异值分解，得到奇异值序列图如图2所示（只显示了80个奇异值中的前30个）。

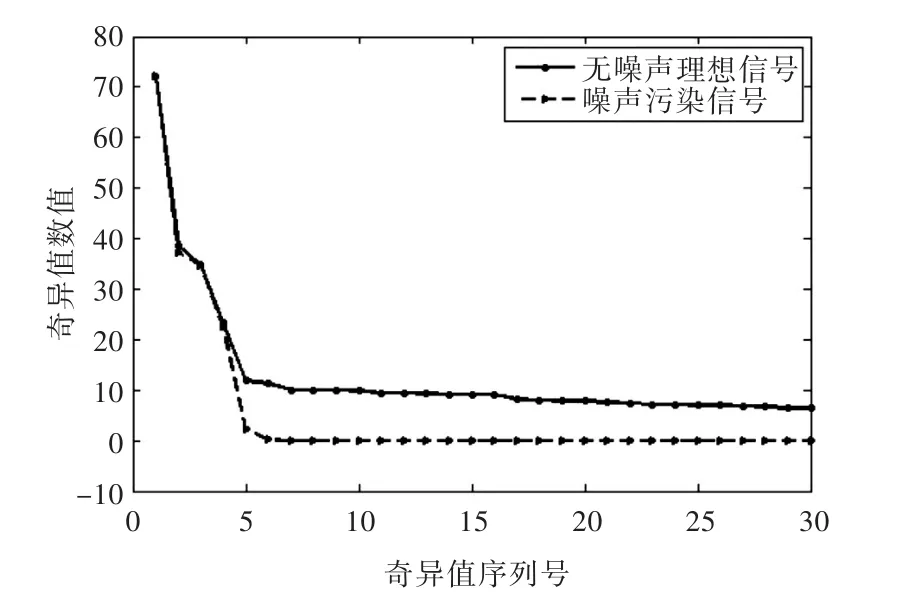
图2 无噪声理想信号和噪声污染信号的奇异值序列图Fig.2 Singular value curves of clean signal and noisy signal

对比图2中的两条奇异值曲线可知，每个奇异值受到噪声干扰的程度不同：较大的奇异值受噪声干扰的影响较小，而较小的奇异值受噪声干扰的影响则较大。由于由受噪声污染信号构造的Hankel矩阵的每个奇异值都是由“有用信号”和“噪声信号”两部分组成，实际选取奇异值数目就是一个对有用信号和噪声信号进行取舍的过程，所以，就要考虑在所选取的数目对应的那个奇异值中，有用信号和噪声信号的比例关系。

3.2 方法对比

3.2.1 奇异值曲线和奇异熵增量

奇异值曲线和奇异熵增量判断有效奇异值数目的方法，分别是以奇异值拟合曲线和奇异熵增量曲线的拐点来作为阈值设置的依据。实际计算结果表明，两种曲线除幅值有所变化外，形状并没有多大区别。

对图1中受噪声污染的信号取维数m＝80，n＝122构造Hankel矩阵，进行奇异值分解，得到奇异值序列图（图3）和奇异熵增量随奇异值数目变化的曲线图（图4）。通过对比，证实上述结论是正确的。

由于降噪效果往往对奇异值的数目很敏感，因此，奇异值数目的微小差别都将导致信号去噪效果有较大差异。上述方法存在的主要问题就是拐点不够清晰，即使存在拐点，选取对应的奇异值数目一般也不能得到最优的降噪结果。采用上述两种方法，并通过观察图3和图4，可以选取奇异值的数目为5。

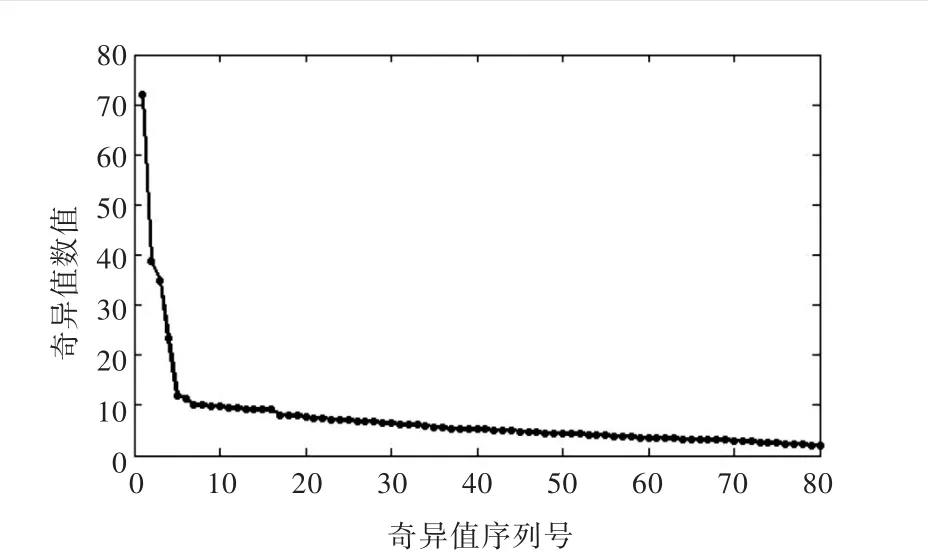
图3 奇异值序列图（噪声污染仿真信号）Fig.3 Singular value curve（noisy simulation signal）

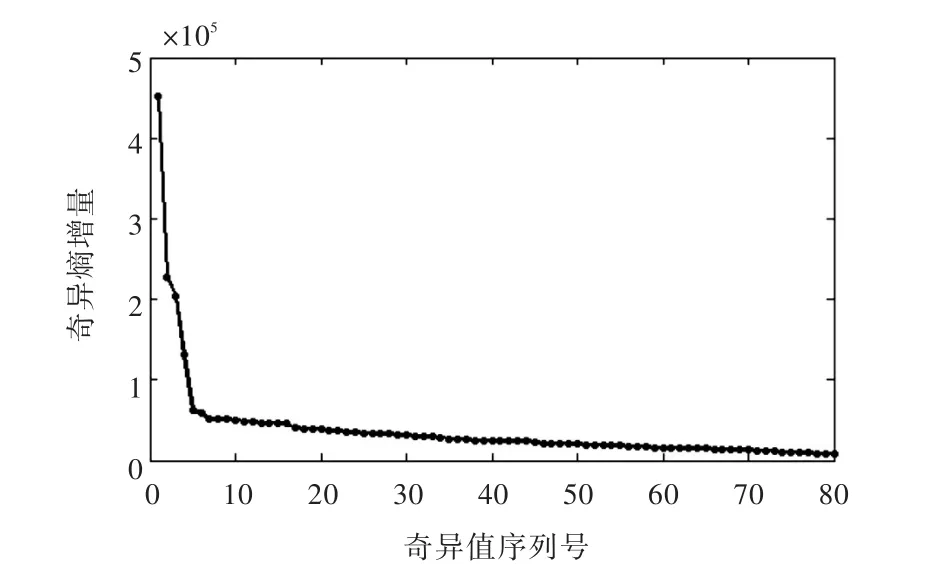
图4 奇异熵增量随奇异值数目变化的曲线图（噪声污染仿真信号）Fig.4 Increment of the singularity entropy versus the number of the singular values（noisy simulation signal）

当选取的奇异值数目为5时，通过计算，得到降噪后的信噪比为18.5 dB。去噪后的信号与无噪声理想信号的对比如图5所示。由图可见，信号中含有很多“毛刺”，尤其是后半段受噪声影响较严重。

图5 奇异值数目为5对应的降噪信号和无噪声理想信号Fig.5 Noise elimination signal with 5 singular values and clean signal

3.2.2 改进方法——极值点数量

现利用改进的方法，采用与第3.2.1小节中相同的维数构造Hankel矩阵，进行奇异值分解。通过计算得到的信号降噪后极值点数量随选取奇异值数目变化的关系如图6所示。极值点数量突变非常明显，要选取的有效奇异值数目为4。

图6 极值点数量随奇异值数目变化图（噪声污染仿真信号）Fig.6 Number of the extremum points versus the number of singular values（noisy simulation signal）

当奇异值数目为4时，通过计算得到降噪后的信噪比为 22.3 dB，相比第 3.2.1小节中用两种方法选取奇异值数目为5时的信噪比（18.5 dB），有明显的提高。降噪信号和无噪声理想信号的对比如图7所示。由图可见，其明显优于图5中的降噪效果。

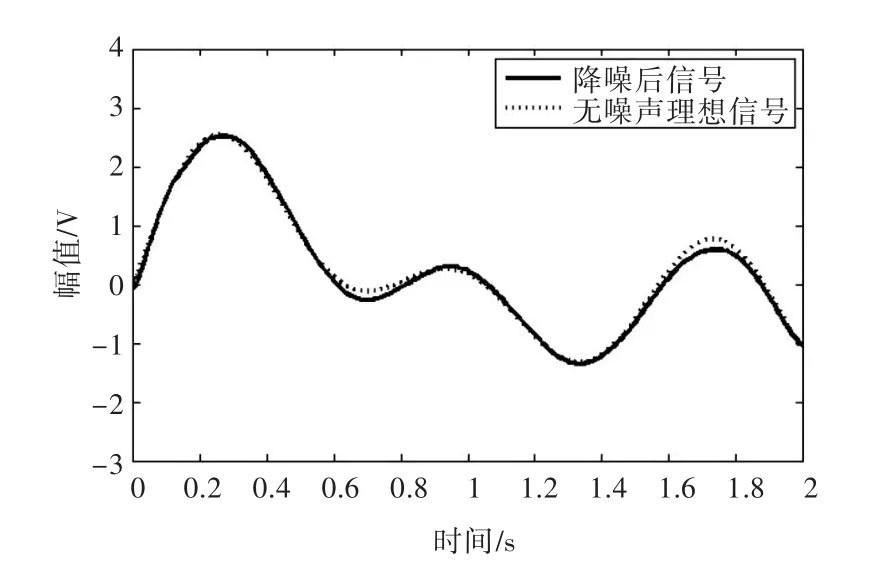
图7 奇异值数目为4对应的降噪信号和无噪声理想信号Fig.7 Noise elimination signal with 4 singular values and clean signal

当奇异值数目小于最佳的选项4时，为使效果更明显，例如，选取1时，其降噪后的信噪比为6.3 dB，相比奇异值数目为 4时的信噪比 22.3 dB，有较大的衰减。去噪后的信号与无噪声理想信号的对比如图8所示。由图可见，降噪信号中没有“毛刺”，但形状有明显的改变，第2和第3个峰值已基本被过滤掉。

图8 奇异值数目为1对应的降噪信号和无噪声理想信号Fig.8 Noise elimination signal with 1 singular value and clean signal

图9所示为奇异值数目从1～8变化时信号降噪后的信噪比曲线图。由图可见，奇异值数目为4时，信噪比最高；当奇异值数目大于或者小于4时，信噪比都有所下降，故4为最优选择。

图9 降噪信号信噪比随选取奇异值数目变化的曲线图（噪声污染仿真信号）Fig.9 Signal to noise ratio versus the number of the singular values（noisy simulation signal）

综上所述，Hankel矩阵有效奇异值数目的确定至关重要，选取不当，就会造成结果偏差较大。当奇异值数目选取过小时，因奇异值的组成中主要是有用信号，噪声的干扰可以忽略不计，所以降噪后的信号中没有噪声引起的明显波动。但由于阈值选取过大，很多包含在奇异值中的有用信号也被剔除掉了，表现为有用信号的损失。当选取最佳的奇异值数目时，不仅过滤掉了大量的噪声，而且还最大程度地保留了原始信号的信息，与原始信号吻合很好。所以，在降噪后剩余噪声对信号没有明显影响的情况下，选取的奇异值数目越大，信噪比越高，就越是接近不受噪声污染的原始信号。当奇异值数目选取过大时，降噪后的信号中仍然含有大量的噪声。例如，奇异值数目选取为5时，与最佳的奇异值数目4相比，虽然仅仅只大1，但信号中却出现了大量的“毛刺”，噪声干扰很明显。使用本文的方法，根据信号降噪后极值点数量的变化，能够清晰地反映剩余噪声对信号的影响，从而确定应该选取的最佳奇异值数目。

4 实验验证

4.1 实测频响函数加高斯白噪声

文献［9］中提到，经过对分别使用频响函数（FRF）和脉冲响应函数（IRF）构造的Hankel矩阵进行奇异值分解降噪的大量研究发现，使用FRF得到的奇异值曲线没有明显的拐点，不容易找到合理的阈值，在判断奇异值分解的有效秩时，使用IRF更具优越性。但是，使用IRF对奇异值进行分解降噪，就需要把FRF先进行逆傅立叶变换，待奇异值分解降噪处理后，再通过傅立叶变换将IRF变换成FRF。

根据降噪后信号极值点数量的突变来判断矩阵的有效奇异值数目，弥补了上述方法的不足，即利用FRF构造Hankel矩阵进行奇异值分解降噪仍能判断出最佳的奇异值数目，避免了正、逆傅立叶变换增加的计算量。

本文通过实验测得了频率范围为0～500 Hz的FRF信号，分辨率为1 Hz。由于实验时随机噪声干扰不大，为了更明确地展示改进方法的有效性，对该实测信号加入了信噪比为15 dB的高斯白噪声。加入了高噪声污染的实测信号如图10所示。

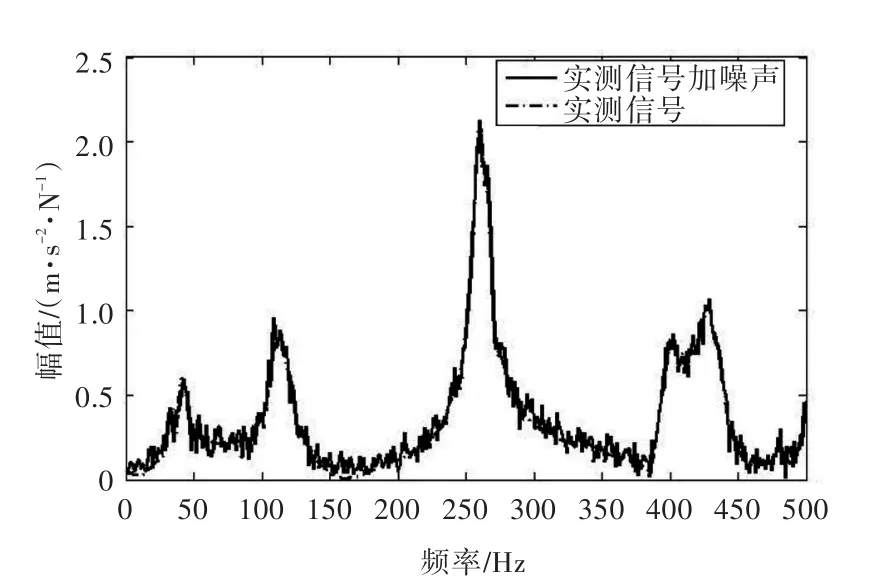
图10 实测频响函数信号与实测频响函数信号加噪声Fig.10 Measured FRF signal and measured FRF signal with additive noise

取m＝210，n＝292构造Hankel矩阵并进行奇异值分解，依照第3.2.1小节中的方法，得到奇异值序列图如图11所示。通过观察图11可发现，奇异值序列图的拐点处呈“弧状过渡区”，有效奇异值数目的选取不明显，无法作出判断。而依照第3.2.2小节中的改进方法，计算得到的极值点数量随选取奇异值数目变化的关系如图12所示，发现29为最优选择。图13所示为降噪后信号与实测信号的对比图，其降噪后的信噪比为20.9 dB。

图11 奇异值序列图（频响函数）Fig.11 Curve of the singular values（FRF）

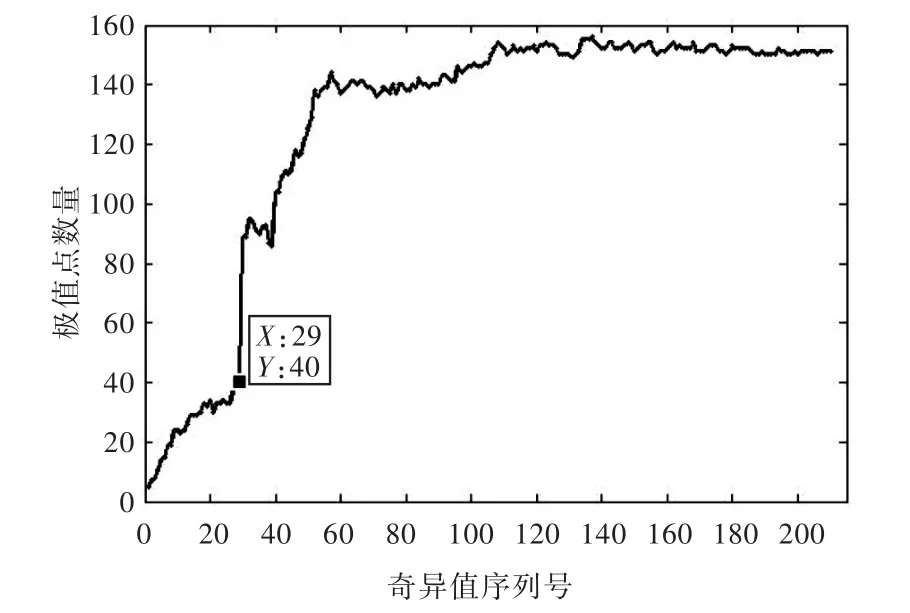
图12 极值点数量随奇异值数目变化的关系图（频响函数）Fig.12 Number of the extremum points versus the number of singular values（FRF）

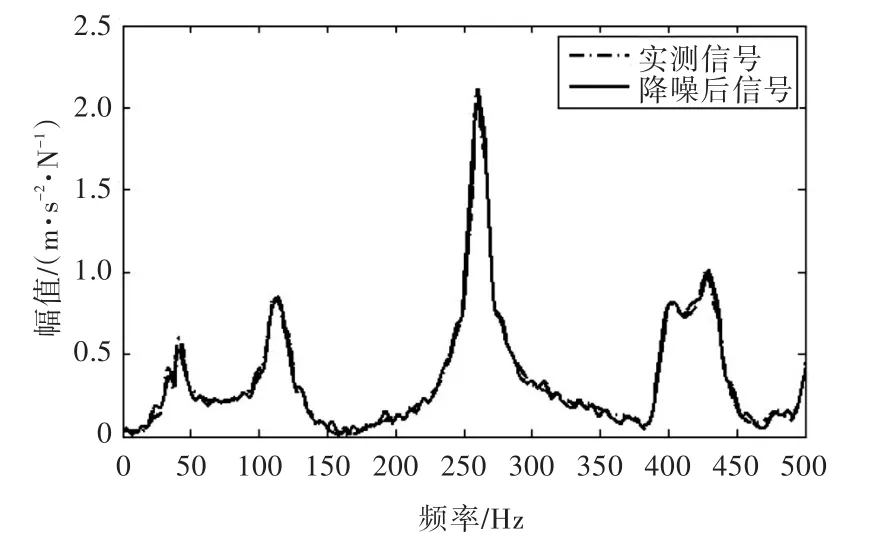
图13 实测信号与奇异值数目为29对应的降噪信号Fig.13 Measured signal and noise elimination signal with 29 singular values

图14所示为奇异值数目从21～38变化时信号降噪后的信噪比曲线图。由图可见，奇异值数目为29时，信噪比最高；当奇异值数目大于或者小于29时，信噪比都有所下降，故29为最优选择。

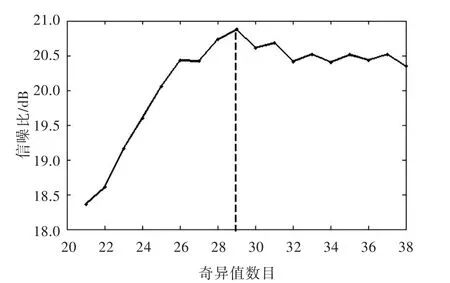
图14 降噪信号信噪比随选取奇异值数目变化的曲线图（频响函数）Fig.14 Signal to noise ratio versus the number of the singular values（FRF）

4.2 实测受噪声干扰自功率谱

图15为受噪声干扰明显的实测加速度自功率谱，频率范围为 0～499 Hz，分辨率为 1 Hz，同样采用第3.2.2中的改进方法进行处理。取 m＝200，n＝301构造Hankel矩阵并进行奇异值分解，通过计算得到的降噪后信号极值点数量随奇异值数目变化的关系如图16所示。由图可见，奇异值数目为11时为最优选择，其降噪后的信号如图17所示。

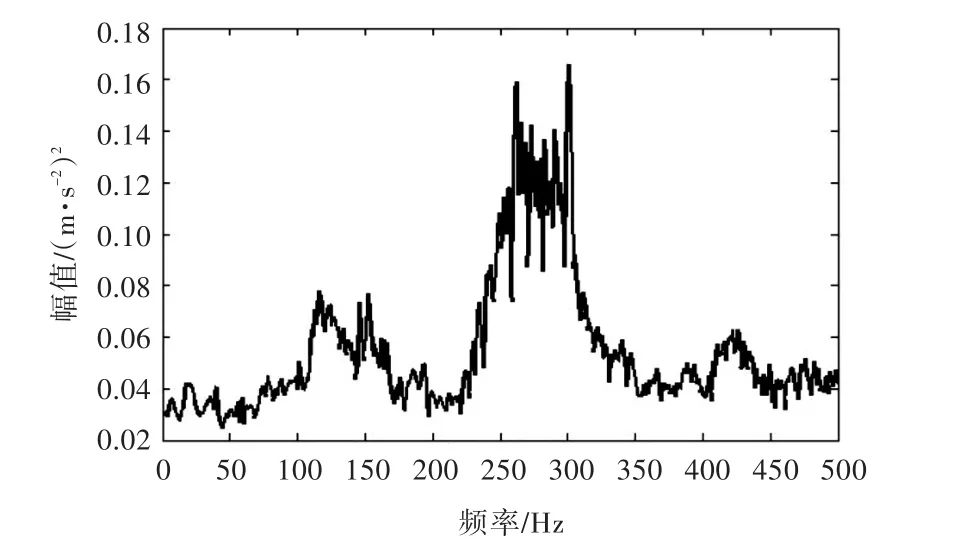
图15 实测受噪声干扰的自功率谱信号Fig.15 Measured noisy autospectrum signal

图16 极值点数量随奇异值数目变化的关系图（自功率谱）Fig.16 Number of the extremum points versus the number of singular values（autospectrum）

图17 奇异值数目为11对应的自功率谱降噪信号Fig.17 Noise elimination autospectrum signal with 11 singular values

5 结 语

目前用于确定奇异值数目的方法，如奇异值曲线、奇异熵增量、信噪比经验等，都不能明确给出有效的阶次，往往只能依赖经验进行选取。本文提出了根据降噪后信号中极值点数量的变化来确定与最优降噪结果对应的奇异值数目的方法。仿真及实验结果表明，该方法准确、有效。在机械设备、船体结构等多种噪声振动工程测试领域，尤其是在面临特殊的测试环境（例如，海浪海风的影响）时，利用该方法对诸如FRF、自功率谱等测试到的信号进行降噪处理能够得到最优的降噪效果，使测试信号具有更高的可靠性，可为正确分析后续信号提供保障。

［1］MARUDACHALAM K，WICKS A L.An attempt to quantify the errors in the experimental modal analysis［C］//The 9th International Modal Analysis Conference.Florence，1991：1522-1527.

［2］JUNG H，EWINS D J.On the use of simulated“experimental”data for evaluation of modal analysis methods［C］//Proceedings of the 10th International Modal Analysis Conference，1992：421-429.

［3］MITCHELL L D.Modal testing methods：quality，quantity and the unobtainable［J］.Sound and Vibration，1994，28（11）：10-17.

［4］FAHEY S O，WICKS A L.Noise sources in mechanical measurements［J］.Experimental Techniques ，2000，24（2）：40-43.

［5］杨文献，姜节胜.机械］［J］.机械工程学报，2000，36（12）：9-13.YANG W X，JIANG J S.Study on the singular entropy of mechanical signal［J］.Journal of Mechanical Engineering，2000，36（12）：9-13.

［6］吕永乐，郎荣玲，梁家诚.基于信噪比经验值的奇异值分解滤波门限确定［J］.计算机应用研究，2009，26（9）：3253-3255.LV Y L，LANG R L，LIANG J C.Decision of threshold for singular value decomposition filter based on SNR’s empirical value［J］.Application Research of Computers，2009，26（9）：3253-3255.

［7］GOLUB G H，VAN C F，LOAN V V.Matrix computations［M］.3rd Edition.Maryland：John Hopkins Studues in Mathematical Sciences，1996.

［8］修春波，刘向东，张宇河.相空间重构延迟时间与嵌入维数的选择［J］.北京理工大学学报：自然科学版，2003，23（2）：219-224.XIU C B，LIU X D，ZHANG Y H.Selection of embedding dimension and delay time in the phase space reconstruction［J］.Journal of Beijing Institute of Technology（Natural Science Edition），2003，23（2）：219-224.

［9］SANLITURK K Y，CAKAR O.Noise elimination from measured frequency response functions［J］.Mechanical Systems and Signal Processing，2005，19（3）：615-631.