发电机组污染排放约束下电量互换合作博弈优化模型
2012-07-06谭忠富董力通刘文彦宋艺航
谭忠富 董力通 刘文彦 于 超 宋艺航
(华北电力大学经济与管理学院 北京 102206)
1 引言
我国是世界第二大能源消费国,随着经济快速发展和人民用电水平提高,我国的用电需求增幅明显,能源供应形势日趋紧张。在能源消耗巨幅增加的同时,也带来了一系列环境污染问题。在我国所排放的污染物中,发电企业的排放量占了很大的比重,发电厂所排放的污染物主要有二氧化硫、氮氧化物、粉尘、废水及固体废物,其中二氧化硫的排放达到了全社会总排量的一半,固体废物的生产量占工业固体废物产生量的20%左右。
近年来我国对污染排放严重的火力发电企业颁布了多项节能减排政策。1996年、2003年两次颁布了《火电厂大气污染物排放标准》,提出了燃煤电厂烟尘、二氧化硫、氮氧化物的排放标准。2003年颁布的《排污费征收使用管理条例》,对各种污染的收费都进行了明确的规定。在2009年的世界气候大会上,我国承诺到2020年单位GDP 碳排放比2005年减少40%~45%[1]。作为工业污染排放大户的电力企业,其污染排放控制效果将直接决定我国减排目标的实现。
发电节能调度是实现火力发电企业节能减排的重要手段,目前已在河南、贵州、四川等省份开展了试点工作。而关于节能调度的研究大多围绕机组组合的节能效果开展,如文献[2]考虑了环境成本、阻塞成本、煤耗以及网络约束,分别以社会效益最大、环境成本最小为目标函数,建立了水火电厂间的发电权交易模型。文献[3]利用二氧化碳的排放量函数代替能耗函数,设计了考虑电力市场与节能调度相互协调的机组组合模型。文献[4]论述了节能调度下兼顾环境保护和经济效益的多目标混合电力系统发电计划模型,提出在节能调度下风、水、火电混合系统的中长期发电计划模型。文献[5]将粗糙集模型应用到河北南网的发电节能调度优化过程中,选出对实现节能降耗有较大影响的指标,对指标进行分析,提出相应的节能降耗措施。文献[6]建立了系统有功网损最小和机组发电耗煤量最小的多目标负荷分配模型。该模型改进了基于Pareto 最优概念的多目标粒子群算法,将其应用于多目标负荷最优分配,能对系统进行整体节能优化。从上述文献分析可以看出,已有的文献多是对于节能调度下机组组合的方法和节能效果进行优化,而对于节能调度下机组组合带来的利益分配却无探讨,本文将污染排放惩罚成本引入到传统的发电经济调度模型中,构建了污染排放成本与发电成本最小化下的合同发电量置换优化模型,并采用合作博弈利益分配的Shapley 模型对合作后所有机组之间利润进行优化分配。
2 发电经济调度优化模型
发电经济调度是指在满足电力系统安全运行及电能质量的前提下,利用资源与设备,以发电成本最小化为目的进行的发电量的转移。在发电经济调度的过程中,需要满足多个约束,调度的最终结果是发电机组之间电量的重新分配,达到整体的成本最小化。
现假设在某一时段内参与发电经济调度的机组有n台,该时段又被分为T段时间,则目标可以表示为

式中,ΔTt为时间段长度,为了讨论上的方便,后面取ΔTt=1,于是可以不再出现;是第i台机组T时间段内的运行成本,这里假设函数关系为;是机组i在T时段内污染物(CO2、NOx)排放量,这里假设函数关系为,κ指发电排放物(CO2、NOx)的单位惩罚费用或者排放税;git是机组i时刻t的出力。
约束条件是:
(1)每个时段所有机组的发电量总和是额定值,记为tD

(2)在相邻时段之间,机组i的发电爬坡速度受到限制
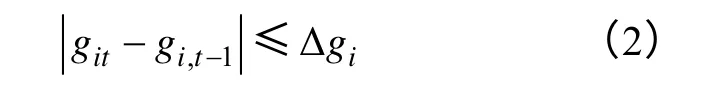
(3)机组i在ΔtT时段内的发电量受到上、下限约束,gimin、gimax是机组i的最小、最大出力限制

(4)机组i的排放污染物总量的限制,2maxiF指机组i在T时段内发电排放物(CO2、NOx)的最大限制
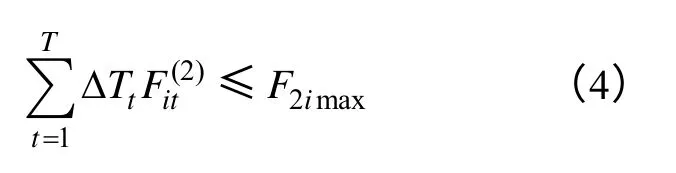
(5)机组i在所有时段内的发电量总和不能低于合同电量Qci

3 发电机组电量互换合作博弈优化模型及利益分配
合作博弈也称为正和博弈,是指博弈双方的利益都有所增加,或者至少是一方的利益增加,而另一方的利益不受损害,因而整体利益增加。合作博弈主要是研究利益的分配问题,因为合作博弈能够产生一种合作剩余,这里所采用的shapley 法就是一种合作博弈模型。
将一组参与者定义为集合N={1,2,…,n},V(S)是N的任意一子集S所对应的函数值,在这里被视为合作者通过合作获得的利益,并且满足条件,V(φ)=0,V(S1∪S2)+V(S1∩S2)≥V(S1)+V(S2),本文中各个厂商之间是相互独立的,所以条件可以写为V(S1∪S2)≥V(S1)+V(S2),则称[N,V]为n人合作对策,V为对策的特征函数。用Xi表示N中第i个成员从合作的最大效益值V(N)中应得到的一份收入,则X=(X1,X2,…,Xn)称为合作博弈对策的分配策略。
如果X满足如下3 个特性:
(2)个体合理性:Xi≥V(i),∀i∈N,其中V(i)是成员i不与其他成员结盟时的收益;
则称分配X为该合作博弈的核,记为C(V)。合作博弈的核可能是空集,也可能是多解。目前解决合作利益分配问题的有效方法是Shapley 值法。
Shapley 值指满足以下3 个公理:
(1)有效性。若成员i对其所参与的合作没有贡献,那么就不应对其进行分配,且所有成员的收益总和等于总收益。可以表达为当V(S-i)=V(S)时,则有
(2)对称性。每一个合作组合中,成员所得利益分配与其记号无关。令π是N={1,2,…,n}的一个排列,若πi为i的对应,πs为S的对应(S⊂N);记V(πs)=U(S),则对于一切i=1,2,…,n有X πi(V)=X i(U)。
(3)可加性。对于集合N上的任意两个特征函数U和V,有X i(U+V)=X i(U)+X i(V),i=1,2,…,n。即n人同时进行两项合作时,该收益应该为两项合作的分配之和。
针对Shapley 值,Shapley 给出了计算合作对策利益分配的模型。
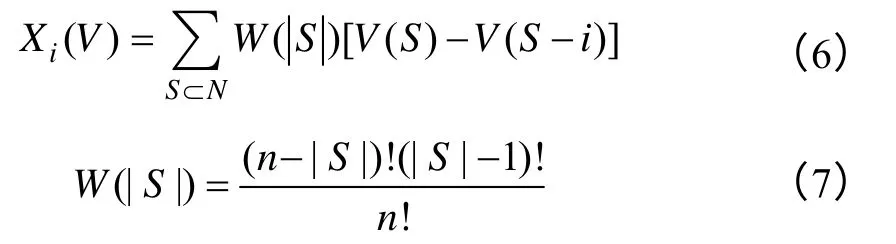
Shapley 值由特征函数V确定,合作博弈的分配策略Xi表达为 式中,S是包含i的所有子集;|S|是子集S中的元素个数;W(|S|)是加权因子;V(S)是包含i的联盟S的合作收益;V(S-i)是不包含i的联盟收益,N={1,2,…,n},i=1,2,…,n。
记I为机组之间在合同电量、排污约束联盟方面的各种方案的集合:I={I1,I2,…,Im},即存在如下的各种联盟方式:
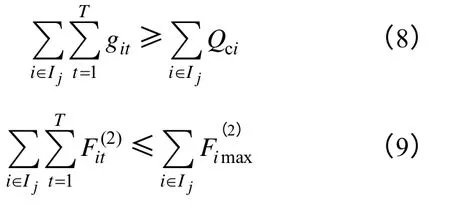
针对每一种联盟方式Ij,分别计算:

对于ji I∈,git需要满足式(8)和式(9);对于ji I∉,git需要满足式(4)和式(5)。
在此基础上,首先计算Ij联盟后,所有发电机组的利润总和

接着计算所有发电机组进行联盟后的利润总和:
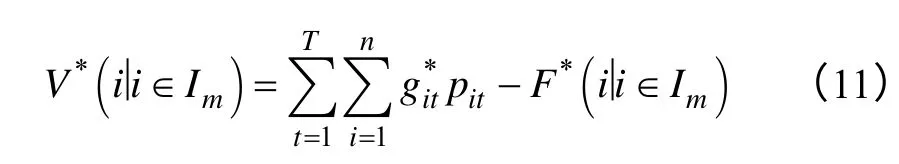
式中,Im={1,2,…,n}。
然后计算,所有发电机组进行联盟后,每台发电机组分配的利润为
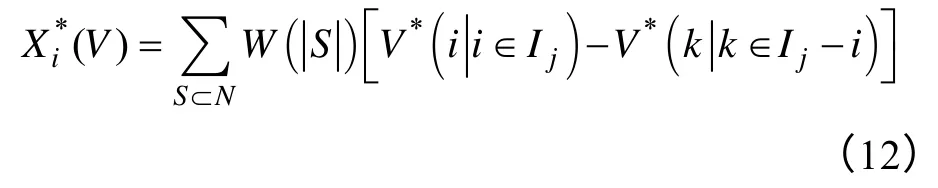
式中,W计算见式(7)。
最后计算,所有发电机组进行联盟后的发电成本与排污成本:

为了更容易理解上述模型,下面针对3 台机组的情况进行具体分析:
(P3)minF*(1,2,3)
s.t.式(1)~式(3)

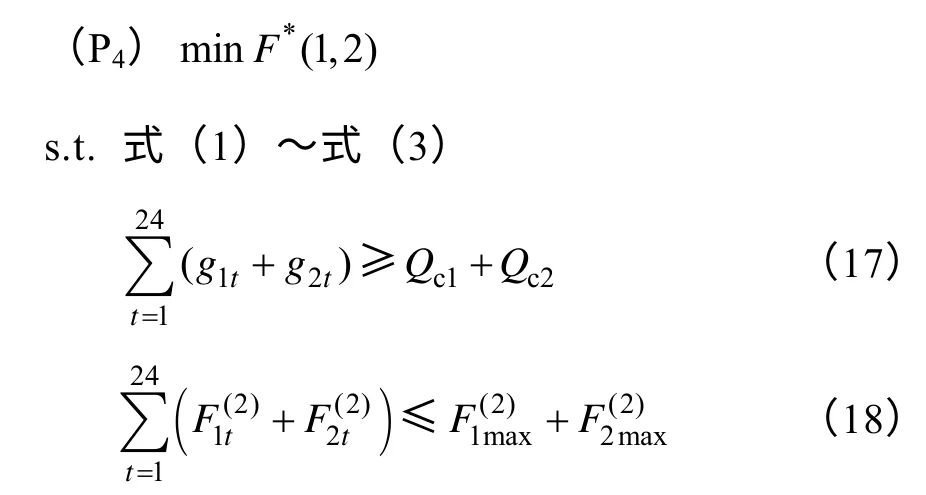
得到V*(1 ,2)。

得到V*(2,3)。


得到*(1,3)V。
机组1 本身独自参加联盟情形下,由于没有合作者,等于没有联盟,故(见式(6))。同理,可以得到:

4 算例
假设现有3 台机组,令T=24h,运用Matlab 进行优化计算。已知 3 台机组的装机容量分别为300MW,600MW,1 000MW,3 台机组的运行成本参数、排污量参数,运行出力的上下限值,每个时段出力允许变化的幅度,每台机组的合同电量信息见表1。三台机组的排污允许总量为4 万t,κ取0.02元/kg,即20 元/t。
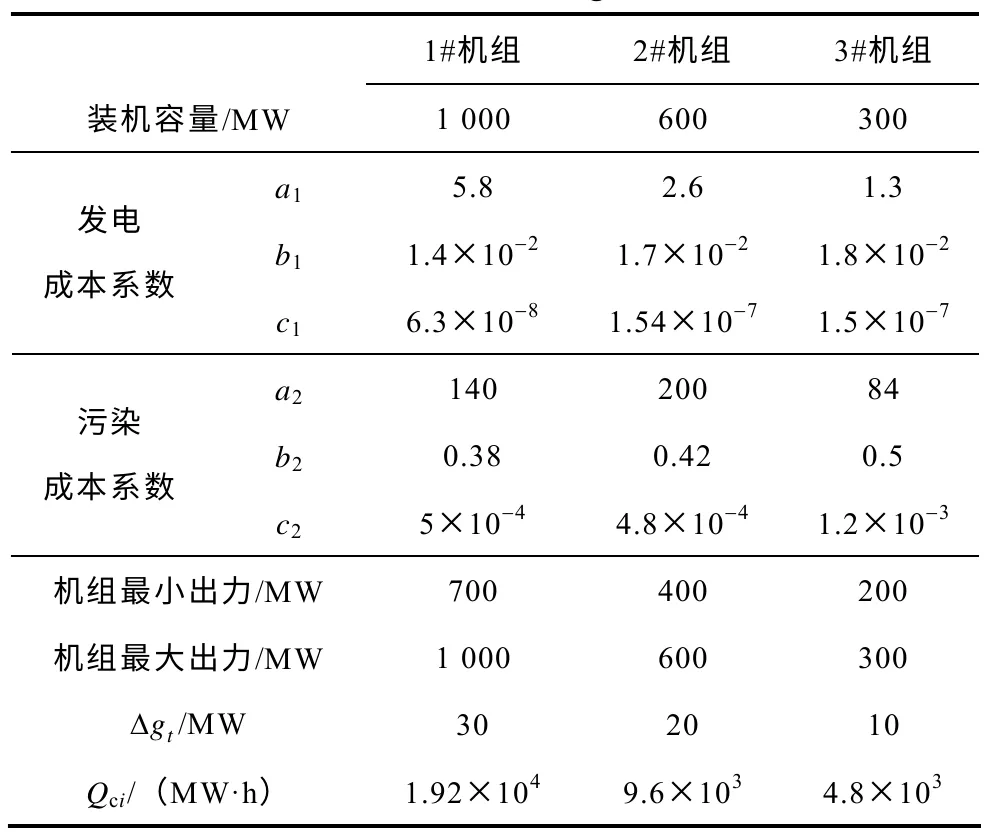
表1 发电机组参数Tab.1 Parameter of generators
当未进行发电量的置换而分配发电量时,3 台机组各自的发电量是用每个时段的总发电量乘以该机组装机容量占总装机容量的比重来决定的,这里没有机组间的电量置换,每个时段的发电量、各台机组的发电量、总的发电量见表2。

表2 机组间发电置换前的调度结果Tab.2 Power output before generation replacement
假设三台机组的上网电价都是相同的且不变,均为0.3 元/(kW·h),根据机组的发电量可以确定机组各自的利润及总利润,见表3。

表3 机组间置换前的发电利润Tab.3 Generation profits before generation replacement
当考虑了污染函数后,重新对这3 台机组进行电量分配的优化求解,优化后的结果,各个机组的发电量、排污总量均满足约束条件,结果见表4。

表4 机组间发电置换后的调度结果Tab.4 Power output after generation replacement
可以计算出考虑污染成本后机组之间的利润,见表5。

表5 机组间电量置换后利润Tab.5 Generation profits after generation replacement
根据所给出的Shapley 法,对3 台机组之间的合作组合进行了计算,分别得出了V*(1,2,3),V*(1,2),V*(2,3),V*(1,3),根据这些组合的结果得到了Shapley 法的最终结果,见表6。
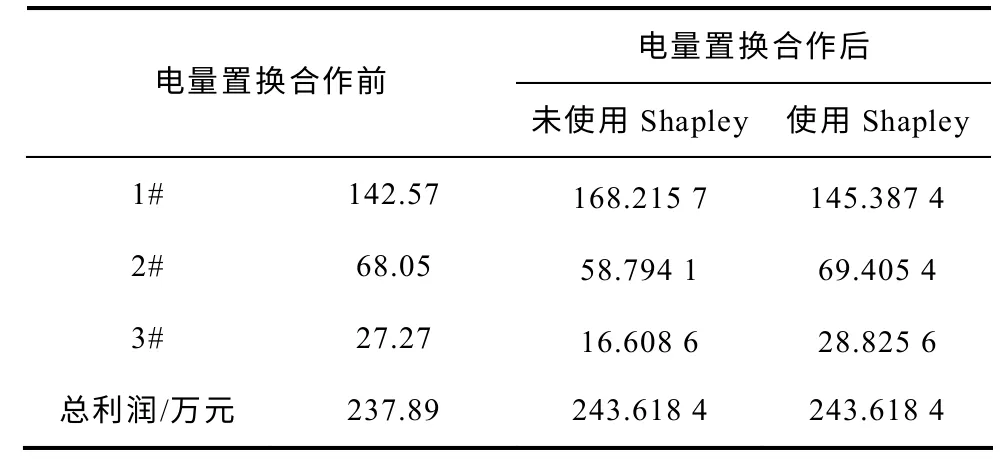
表6 机组间合作前后利润分配结果对比Tab.6 Profits distribution results of units cooperation
通过计算,发现发电量从总成本高的机组转移到了成本低的机组上,2 号机组共转移了830.53MW·h的电量到1 号机组上,3 号机组共转移了1 085.26MW·h的电量到1 号机组上,这使得三台机组的利润发生了变化,1 号机组的利润增加了25.65 万元,2、3 号机组的利润一共减少19.92 万元,三台机组的总利润增加了5.73 万元,这说明发电量的置换对整体有益。当运用Shapley 法对所得收益进行分配后,三台机组与未进行合作时相比分别增加了2.82、1.36、1.55 万元,合作为三台机组都带来了利益的增加。
5 结论
本文在考虑机组污染成本的前提下进行机组发电量的置换,这是一种合作的方式。本文首先建立了考虑污染成本情况下的置换优化模型,然后运用合作博弈模型对合作的盈利进行了分配,使参与的各方的收益都有所增加,通过分析可以得出以下结论:
(1)在成本导向的前提下,通过合作进行的电量置换可以减少总体运营成本,使发电企业获取更多利润。
(2)在降低成本的同时,污染物的排放也会相应减少,该机制不仅促进了机组节能减排积极性,还推动了高能耗、高污染机组退出市场。
[1]中华人民共和国国务院新闻办公室.中国的环境保护(1996-2005).www.gov.cn/zwgk/2006-06/05/content_ 300288.htm.
[2]陈赟,严正.考虑节能减排与网络约束的发电权交易模型[J].电力系统保护与控制,2009,37(12):52-57.Chen Yun,Yan Zheng.Generation rights trade model based on energy-saving,emission-reducing and network constraint[J].Power System Protection and Control,2009,37(12):52-57.
[3]徐致远,罗先觉,牛涛.综合考虑电力市场与节能调度的火电机组组合方案[J].电力系统自动化,2009,33(22):14-17.Xu Zhiyuan,Luo Xianjue,Niu Tao.Thermal unit commitment scheme considering electricity market and energy-saving dispatch[J].Automation of Electric Power Systems,2009,33(22):14-17.
[4]温丽丽,刘俊勇.混合系统中、长期节能调度发电计划的蒙特卡罗模拟[J].电力系统保护与控制,2008,36(24):24-29.Wen Lili,Liu Junyong.Monte Carlo simulation of medium and long-term generation plan in hybrid power system based on environmental/economic dispatch[J].Power System Protection and Control,2008,36(24):24-29.
[5]邹颖.河北南网发电节能调度优化研究[D].保定:华北电力大学(河北),2007.
[6]苏鹏,刘天琪,赵国波,等 基于改进粒子群算法的节能调度下多目标负荷最优分配[J].电网技术,2009,33(5):48-53.Su Peng,Liu Tianqi,Zhao Guobo,et al.An improved particle swarm optimization based multi-objective load dispatch under energy conservation dispatching[J].Power System Technology,2009,33(5):48-53.
[7]Li Shujin,Zhang Qiang.A simplified expression of the Shapley function for fuzzy game[J].European Journal of Operational Research,2009,196(1):234-245.
[8]喻洁,李方兴,李扬,等.互联区域多目标发电调度的协同优化策略[J].电力系统自动化,2009,33(2):30-33.Yu Jie,Li Fangxing,Li Yang,et al.A coordinated optimization strategy for multi-objective generation dispatch in interconnected areas[J].Automation of Electric Power Systems,2009,33(2):30-33.
[9]谢国辉,张粒子,邵志刚,等.改进Shapley 值在协同报价利润分配中的应用[J].华东电力,2009,37(2):232-235.Xie Guohui,Zhang Lizi,Shao Zhigang,et al.Application of improved Shapley value to profit distribution for collaborative bidding[J].East China Electric Power,2009,37(2):232-235.
[10]谭忠富,陈广娟,赵建保,等.以节能调度为导向的发电侧与售电侧峰谷分时电价联合优化模型[J].中国电机工程学报,2009,29(1):55-60.Tan Zhongfu,Chen Guangjuan,Zhao Jianbao,et al.Optimization model for designing peak-valley time-of-use power price of generation side and sale side at the direction of energy conservation dispatch[J].Proceedings of the CSEE,2009,29(1):55-60.
[11]Abido M A.Environmental/economic power dispatch using multi-objective evolutionary algorithms[J].IEEE Transactions on Power Systems,2003,18(4):1529-1536.
[12]尚金成.基于节能减排的发电权交易理论及应用(一)发电权交易理论[J].电力系统自动化,2009,33(12):46-52.Shang Jincheng.Generation right exchange theory and its applications based on energy-saving and emission-reducing part one generation right exchange theory[J].Automation of Electric Power Systems,2009,33(12):46-52.
[13]喻洁,李扬,夏安邦.兼顾环境保护与经济效益的发电调度分布式优化策略[J].中国电机工程学报,2009,29(16):63-68.Yu Jie,Li Yang,Xia Anbang.Distributed optimization of generation dispatch schedule considering environmental protection and economic profits[J].Proceedings of the CSEE,2009,29(16):63-68.
[14]彭春华.综合环境保护及竞价风险的发电侧经济运行[J].中国电机工程学报,2008,28(28):97-102.Peng Chunhua.Economic operation problem of generating side considering environmental protection and bidding risk[J].Proceedings of the CSEE,2008,28(28):97-102.
[15]谭忠富,李莉,王建军,等.多智能体代理下电力双边谈判中的模糊贝叶斯学习模型[J].中国电机工程学报,2009,29(7):106-113.Tan Zhongfu,Li Li,Wang Jianjun,et al.A fuzzy bayesian learning model in agent-based electric power bilateral negotiation[J].Proceedings of the CSEE,2009,29(7):106-113.
