220kV垂直双分裂导线粘连机理仿真
2012-07-06何小新喻剑辉周文俊
张 飚 何小新 喻剑辉 胡 蓉 杨 丹 周文俊
(1.武汉大学电气工程学院 武汉 430072 2.武汉大学动力与机械学院 武汉 430072)
1 引言
垂直排列双分裂导线粘连是指由于外界因素引起子导线间的距离变小,在输送大电流时如果受到大风、覆冰或者高温气候影响,分裂子导线局部会在瞬时十分接近,导致子导线之间的电磁吸引力加大,当吸引力大到某一程度时便会引起子导线局部粘连,而局部粘连又使紧靠粘连点的子导线之间的距离进一步缩小,相互间的电磁力加大,导致粘连不断延伸,直至导线悬挂处。分裂导线粘连后,电晕起始电压降低,线路局部对地电容减小、感抗增大,导致输电线路线损增加,输送能力降低。同时子导线粘连过程中的鞭击也容易导致导线磨损,甚至引起断股、断线事故,危害输电线路的安全运行。由于垂直排列双分裂导线输电线路具有不需间隔棒等优点,在无覆冰地区220kV 输电线路上得到广泛应用,但是近年来随着电力负荷的增长、气候条件的变化,垂直排列双分裂导线粘连故障时有发生,广东、浙江、云南、江西、福建、江苏等省市相继报道了所在地区220kV 垂直双分裂输电线路出现的子导线粘连现象,严重影响了电力生产安全。因此,开展对220kV 垂直排列双分裂导线粘连机理的研究具有实际意义。
针对垂直双分裂导线粘连现象,国内电力生产部门、科研机构和高等院校先后展开了研究,对于导线粘连的形成及影响因素有了一定的认识。广东省东莞、佛山供电局的研究表明大风、子导线材质、温差差异、负荷电流和分裂导线间间距等是子导线发生粘连故障的影响因素[1,2]。武汉大学和华南理工大学研究人员分别利用数学模型分析了多种因素对子导线伸长和最小间距的影响,计算了不同条件下子导线粘连的临界电流值[3,4]。福建省电力勘测设计院和福州电业局分析了子导线粘连产生的原因和对电网的影响,提出处理或预防子导线粘连的措施[5-7]。浙江省电力设计院提出了导线粘连的稳定区与不稳定区的概念,考虑了静电排斥力以及悬垂线夹对粘连的影响[8,9]。云南[10]、宁夏[11]、江苏[12]、江西[13]和广东[14,15]等地的电力生技部门也针对具体线路的粘连原因进行了分析和研究。
由于垂直双分裂导线粘连现象是一个涵括电磁学、热学和力学的复杂问题,有关这一现象的机理研究并不成熟,已有的研究多为定性分析,也未开展实验研究。国外对于载流导体之间的相互吸引力和排斥力计算的基本原则已经形成[16,17],但目前尚未见到针对双分裂导线粘连现象的试验研究成果,因此有必要对以上研究工作的不足进行补充和深入。
本文以220kV 垂直双分裂输电线路的耐张段为研究对象,基于悬链线方程和应力状态方程对分裂导线建立粘连数学模型,利用云南省 220kV粘连线路的现场调研结果,结合在户外大型试验场的试验观测数据对数学模型进行校验与修正,应用Matlab 开发220kV 垂直双分裂导线粘连故障仿真软件,分析导致粘连的各项因素,获得不同档距、高差、弧垂、子导线间距以及外力作用下的导线粘连的临界电流。为线路设计和故障线路的改造提供技术支持,保障电力生产的安全运行。
2 垂直双分裂导线粘连的数学模型
双分裂导线粘连标志为上、下子导线十分接近甚至相碰。两者之间的距离可用两导线的弧垂差来表示,它取决于档距内上、下子导线的悬垂函数和应力状态方程。本文以220kV 垂直排列双分裂输电线路的耐张段作为仿真研究的对象,根据耐张段的结构特点,细分为连续档和孤立档两种类型,分别建立数学模型反映子导线间的实际间距与相关要素的关系,获得不同条件下子导线粘连的临界电流值。
2.1 连续档垂直双分裂导线
对耐张段间悬挂悬垂绝缘子串的直线杆塔的连续档中,由于两塔间距较大,导线刚性对导线悬垂状态影响相对变小,可将导线假定为一柔索,其上作用的荷载均指向下方且沿导线长度均匀分布,如图1 所示,由此导出架空线悬垂函数为悬链线型,它的近似式为斜抛物线公式,即假定导线比载γ沿两悬挂点的连线均匀分布。记两悬挂点间的高差为h,垂直于比载作用方向的投影距离为档距l,两悬挂点连线与X轴间的夹角为高差角β,导线轴线应力的水平分量为σ0,则坐标原点位于左侧悬挂点处的斜抛物线方程为[18]


图1 架空电线近似为斜抛物线的受力图Fig.1 Force diagram of overhead transmission line(tilt parabola)
不同气象条件下的导线应力变化可通过应力状态方程计算,即已知某一气象条件下的导线应力、比载、气温及待求气象条件下的比载、气温时,利用导线的弹性伸长及温度伸长在两种气象状态下原始线长不变的原则,求得待求气象条件下的导线应力。考虑到同一耐张段内各连续档的导线水平应力是按照同一值架设的,当气象条件变化时,由于各档的档距及高差不一定相同,各档应力变化就不完全相同,从而使直线杆塔上出现不平衡张力差,使悬垂绝缘子串产生偏斜,偏斜结果又使各档应力趋于基本相同,该应力为耐张段内的代表应力。基于以上考虑得到档距中央斜抛物线近似应力状态方程式为[19]

式中,下标m,n分别表示已知状态和待求状态下的参数;σc、t分别表示档距中央的导线应力和环境温度;E、∂表示导线的弹性系数和温度伸长系数;lr、βr分别为耐张段内的代表档距和代表高差角;
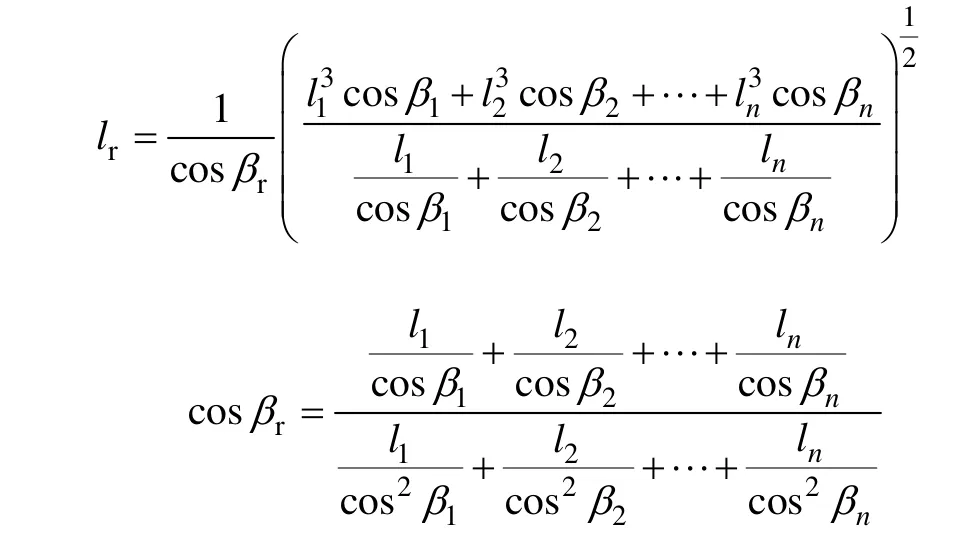
li和βi分别为耐张段内各档的档距和高差角(i=1,…,n)。
连续不等高档的档距中央最大弧垂为
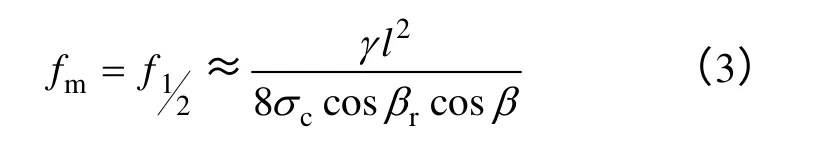
式中,l和β分别为该计算档的档距和高差角。
2.2 孤立档垂直双分裂导线
大跨越、大高差档多采用孤立档,即档距两端为耐张型杆塔,导线两端用耐张线夹通过耐张绝缘子串悬挂在杆塔上,该档导线弧垂、应力不受邻档的影响。由于耐张绝缘子串的单位荷载远大于导线的单位荷载,会对导线的应力、弧垂、线长计算产生影响,对孤立档的计算,做如下假设[20]:
(1)导线和耐张绝缘子串为理想柔索。
(2)导线两侧耐张绝缘子串相同,实际长度为λ,其水平投影长度为λ0=λcosβ。荷载G均匀分布。
(3)导线单位长度上的比载γ沿两悬挂点连线均匀分布,并假定导线所占档距l1=l-2λ0保持不变。
当孤立档两端具有等长等荷载耐张绝缘子串,由于两端的耐张绝缘子串水平投影长度相差很小,且保持各自的荷载不变,档距中央弧垂为

式中,γs为绝缘子串比载,γs=G/(λA);A为导线截面积。
当仅一段有耐张绝缘子串,档距内的最大弧垂处的xm及fm为

当两种状态均为无风或低风速的气象条件时,不考虑施工过牵引及杆塔挠度的因素,按斜抛物线方程求得导线的应力状态方程式为[21]

式中,下标m、n分别表示已知状态和待求状态下的参数;K为线长参数,当两端具有等长等荷载耐张绝缘子串时:

仅一段有耐张绝缘子串时
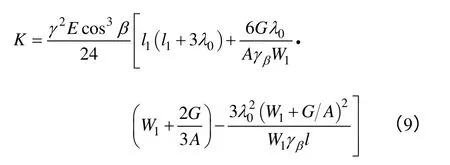
式中,γβ为导线水平投影比载,γβ=γ/cosβ;W1为导线单位截面上的荷载,W1=γl1/cosβ。
2.3 电磁力比载
在弧垂与档距比较小的情况下,将上、下两子导线近似为两根完全平行的直导线。则在垂直排列的双分裂导线中分别通过同向电流I1和I2时,子导线单位长度、单位截面上所受的电磁力比载γd为[22]

式中,d为子导线之间的距离。
仿真计算中假设电磁力沿竖直方向并沿导线均匀分布。则上、下子导线电磁力比载大小相等,方向相反,与导线自重比载γg叠加后可分别求出上、下子导线总比载。

2.4 覆冰比载
输电导线覆冰后,在竖直方向比载增大,覆冰比载为

式中,b为覆冰厚度;D为导线外径。
3 仿真计算过程
3.1 计算流程和粘连判断标准
临界粘连电流采用迭代法求解,其计算流程为:
(1)选定初始状态的比载(不包括电磁力比载)和水平应力作为迭代初始点。初始点在迭代过程中始终保持不变。
(2)当导线中通过一定大小的电流增加时,电磁力比载增加,通过应力状态方程式求出新状态下档距中央导线应力值,再根据新状态下比载及应力值,利用悬链线方程,分别计算两子导线弧垂和最低点间距,随着子导线间距的变化,上、下子导线的电磁力比载将发生变化。重新计算两子导线弧垂及间距值,在新的间距值下求解电磁力比载及相应的导线应力,直至两子导线间距值d收敛。
式中,d0为子导线间距初始值;fmup和fmdown分别为上、下子导线档中弧垂。
流程(2)判断收敛后的子导线间距值,若大于单导线直径,则导线未粘连,增加电流,转入流程(2)循环计算;否则导线粘连,计算结束。
3.2 电磁力比载修正系数
3.2.1 分量的影响修正系数Kup、Kdown
由于上、下两子导线之间电磁力比载的实际方向垂直于导线的切线方向,其水平分量的存在将改变导线应力的水平方向分量,导致上子导线弧垂增大,而下子导线弧垂减小,加速双分裂子导线之间的粘连。因此在原计算模型的基础上引入电磁力比载水平分量影响系数Kup、Kdown分别对上、下子导线弧垂计算,式(3)、式(4)和式(6)进行修正,如式(6)修正式如下:
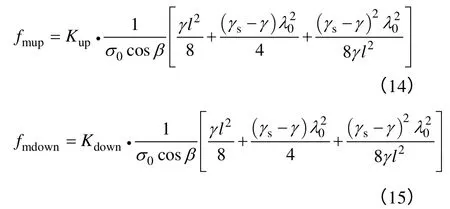
根据试验数据,在电流为 1 000A 时,Kup=1.012 5,Kdown=0.987 5,则

利用系数Kup、Kdown可分别对上、下子导线弧垂计算值进行修正以考虑电磁力比载的水平分量对水平应力的影响,该系数是基于LGJ—300/40×2导线真型试验数据得出,导线规格不同时,电磁力比载水平分量对水平应力的影响大小不同,Kup、Kdown的取值应根据试验数据决定。
3.2.2 动载系数K2
从临界粘连电流求解流程来看,每次迭代的初始点不变,由电磁力比载的改变,求解新的平衡状态下的应力及弧垂。这一静态计算的过程,并未考虑导线在粘连过程中具有一定的惯性及动量。实际情况下的导线粘连从静止状态到相向运动,以及相向运动后恢复到静止状态,是一个动态过程,因此,静态计算将造成临界粘连电流值偏大。在模型中引入动载系数对电磁力比载进行修正,基于 LGJ—300/40×2 导线真型试验数据取K2=1.1,则

4 模型验证与仿真计算结果
4.1 真型试验平台构建
为了验证与修正粘连数学模型,在国网电力科学研究院(武汉)户外试验场搭建了双分裂导线粘连真型试验平台,进行了多种工况下导线粘连试验。
考虑到220kV 输电线路的电力负荷大,很难直接在电网上进行试验,必须考虑等效的试验方法。在户外大型试验场搭建与实际输电线路一致的双分裂输电线路试验段,通过串联电容器全补偿使试验线路基本呈电阻性,利用0~1 500A 连续可调的电源向垂直双分裂导线供电,在低电压下进行大电流的导线粘连试验,再现垂直双分裂输电线路粘连过程,测量临界粘连电流,分析导线弧垂、子导线间距、高差、导线振动等因素对导线粘连的影响。
试验用耐张段的两门型塔塔距为230m,两端悬挂点高差 0~60m 可调,双分裂导线的型号为LGJ—300/40,线路弧垂、高差、子导线间距等参数根据试验方案的安排进行调整。试验所用主要设备包括:250kVA(380V/0~380V)移卷式调压器、CXB—17.5 升流器多台、BKMJ 0.88—117—1 和BZMJ0.45—30—1 补偿电容器多台、电流互感器、T24—A.V 电磁式电流表、YE3817 拉压力传感器、DSZ2 水平仪、YJV22—8.7/15 1×50 电力电缆、RCCR3ILRSCL2 红外测温仪、FFJQ—405 间隔棒多个、钳形电流表、示波器等。试验持续近1 个月,部分试验结果见表1。
4.2 数学模型验证
在同样条件下利用垂直双分裂导线粘连的数学模型进行了仿真计算,结果见表1。

表1 不同工况下的真型试验数据与计算结果比对Tab.1 Comparison of the prototype model test and calculation of different working condition
由表1 可见,各个工况下临界粘连电流计算值与试验值误差不超过15%。误差产生的原因有模型和试验数据误差两方面:悬链线模型将导线假定为一根处处铰接的柔软链条,而实际上钢芯铝绞线的刚性在粘连过程中起到了一定的作用,上述假定在一定程度上影响计算结果的精确性;试验观测数据受环境和条件的影响,如测导线温度的水银温度计和红外测温读数不一致,回路总电流与子导线电流之和不一致等,甚至在同一天进行的两组试验,上午和中午进行初始弧垂测量时的环境温度差别较大,加之中午时导线通流后发热,导致导线温度高于环境温度,而导线温度对弧垂有明显的影响,这些都影响了观测数据的准确性。
4.3 计算结果与讨论
以双分裂导线LGJ—300/40×2 为例,对临界粘连电流与相关因素的定量关系进行仿真计算。
子导线间距与临界粘连电流的关系曲线如图2所示。从图2 可见,在连续档内,无风或微风,高差为0,档距依次为100m、200m、300m 时,随着子导线间距增大,临界粘连电流随之增大,随着档距的增大,临界粘连电流减小。
导线在不同档距下临界粘连电流计算结果如图3 所示,随着档距增大后,临界粘连电流逐渐减小。在档距较小时,临界粘连电流随档距增大而减小的幅度更大。

图2 子导线间距与临界粘连电流关系曲线Fig.2 Bundle spacing critical adhesion current relation curve
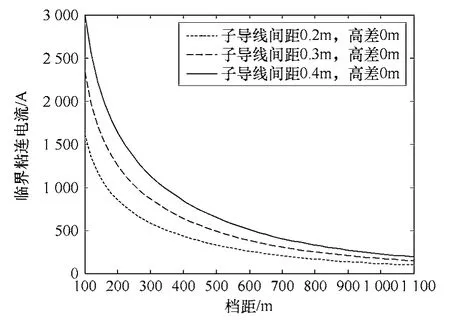
图3 输电线路档距与临界粘连电流关系曲线Fig.3 Transmission line span critical adhesion current relation curve
临界粘连电流与高差的关系曲线如图4 所示。从图4 可见,在档距为250m 连续档内,子导线间距分别为0.4m、0.3m 时,临界粘连电流与高差的变化关系曲线近似平行。随着高差从0 增大至125m,临界粘连电流减小的程度不足150A。而子导线间距从0.4m 减小至0.3m,临界粘连电流减小约300A。由此可知子导线间距较高差对临界粘连电流的影响更大。

图4 导线的高差与临界粘连电流关系曲线Fig.4 Altitude difference critical adhesion current relation curve
临界粘连电流与环境温度关系曲线如图 5 所示。从图5 可见,档距为250m 连续档,子导线间距为0.4m,高差分别为0m、50m 和100m 时,随着环境温度升高,临界粘连电流逐渐减小,但是减小的幅度并不大。环境温度从-10℃上升至40℃,临界粘连电流减小幅度不超过100A。在高差较大时,临界粘连电流随环境温度变化的更大。

图5 不同环境温度下的临界粘连电流Fig.5 Ambient temperature critical adhesion current relation curve
在不同程度的覆冰情况下临界粘连电流与子导线间距关系计算结果如图6 所示。从图6 可见,覆冰后临界粘连电流有所减小,但是减小的幅度不大。随着子导线间距的增大、覆冰厚度加大时,临界粘连电流在减小。

图6 覆冰后临界粘连电流与子导线间距关系曲线Fig.6 Icing bundle spacing critical adhesion current relation curve
利用另一种导线LGJ—500/45×2 进行的计算表明,在其他条件完全相同时,LGJ—500/45×2 导线的临界粘连电流较LGJ—300/40×2 导线略大,而且随着档距、子导线间距的减小,两种型号导线的临界粘连电流趋于接近。
仿真分析表明,尽管影响分裂导线粘连的因素很多,但归根结底是作用于子导线上的附加载荷。电流、子导线间距以及覆冰决定导线比载的大小。环境温度、电流、散热条件影响导线温度的高低,而导线温度变化则改变弧垂。档距、高差、设计弧垂以及弧垂施工误差则反映在导线张力与比载的变化上。
5 应用实例
云南省电网公司普洱供电局220kV 墨戈II 回线N231—N232 档运行中发生粘连,停电后粘连故障仍然不能排除,需要进行改造,决定根据仿真计算的结果形成线路改造的技术方案。
该档两端为直线塔,导线型号为LGJ—500/45×2,档距1030m,高差168.8m,设计弧垂72.6m,粘连相为C 相,塔头绝缘子型号U70BP,粘连时的负荷约140MW。对故障线路进行初步分析确定在人工排除故障后,再加装间隔棒以防止其再次粘连,同时起到抑制档内导线微风振动的作用。通过加装阻尼间隔棒来同时抑制档内导线微风振动和防止粘连故障的再次发生是一种有效的方法,但如何用最少的间隔棒达到抑制档内导线微风振动和防止粘连故障是技术改造方案的关键。
对云南省普洱供电局220kV 垂直双分裂输电线路采用的导线LGJ—500/45×2 进行加装间隔棒的计算,按最大次档距计算,该导线最大运行电流为1 500A,热温极限电流为1 830A,计算过程基于以下几点假设:
(1)加装间隔棒后,间隔棒安装处上下子导线间距值固定。
(2)按照最恶劣的情况进行计算,即加装间隔棒后次档距内的子导线最小间距值等于安装前子导线最小间距值。
(3)线路实际运行电流不应大于线路最大允许运行电流。
基于以上假设,计算各种工况下满足临界粘连电流小于线路最大运行电流的最大次档距,即临界次档距。计算结果见表2。由表2 数据可以得出在子导线间距分别为0.1m、0.2m、0.3m 和0.4m 时,临界次档距依次取90m、180m、260m、340m。

表2 LGJ—500/45×2 导线最大次档距计算Tab.2 Transmission line LGJ—500/45×2 subspan maximum calculation
运行单位应在人工排除故障后,根据子导线间距实测值,对应表3 选择合适的布置方式,加装间隔棒以防止其再次粘连。若人工排除故障后子导线间距小于0.1m,此时子导线间距已经严重不满足设计要求。建议运行单位采用分别调整上、下子导线弧垂的方式,将子导线间距调整到设计值0.4m。
以方案3 为例,墨戈II 回线N231—N232 档间隔棒的布置如图7 所示。

表3 三种技术改造方案比较Tab.3 Comparison of 3 disposing methods

图7 墨戈II 回线N231-N232 档间隔棒安装位置示意图Fig.7 Mo-Ge transmission line II N231-N232 spacers setup
6 结论
(1)本文进行的试验和仿真对现有研究的不足进行了的深入补充。
(2)本文以试验观测、理论分析和计算机仿真相结合,分析垂直双分裂导线粘连机理,建立了双分裂导线粘连数学模型,并基于试验结果进行模型修正,开发出220kV 垂直双分裂导线粘连故障模拟分析软件。
(3)粘连故障线路技术改造应用实践表明,根据仿真结果提出的改造方案具有很好效果,得到运行部门的好评,也验证了本文建立数学模型和计算方法的有效性。
[1]杨挺.220kV 输电线路垂直双分裂导线粘连成因及处理方法[J].广东电力,2005,18(1):58-61.Yang Ting.Cause analysis and disposal route of vertical-arrayed double-bundled transmission line[J].Guangdong Electric Power,2005,18(1):58-61.
[2]杨兆安,武利会.220kV 输电线路垂直双分裂导线粘连的原因分析[J].广东电力,2005,18(12):72-74.Yang Zhaoan,Wu Lihui.Cause analysis of 220kV vertical-arrayed twin-bundled transmission line conglutination[J].Guangdong Electric Power,2005,18(12):73-74.
[3]刘正权,霍锋.220kV 垂直排列双分裂导线粘连现象分析[J].高电压技术,2006,32(11):61-63.Liu Zhengquan,Huo Feng.Analysis on vertical-arrayed double-bundled transmission line conglutination phenomena of 220kV transmission line[J].High Voltage Engineering,2006,32(11):61-63.
[4]雷鸣,刘刚,杨挺.220kV 架空分裂导线的应力动态分析[J].电工电能新技术,2009,28(3):50-53.Lei Ming,Liu Gang,Yang Ting.Dynamic analysis on stress of overhead vertical-arrayed double-bundled transmission line[J].Advanced Technology of Electrical Engineering and Energy,2009,28(3):50-53.
[5]余朝胜.浅析220kV 输电线路垂直双分裂导线粘结问题[J].电力设计,2006(2):48-51.Yu Chaosheng.Analysis of lead felting in 220kV vertical-arrayed double-bundled transmission lines[J].Electric Power Survey & Design,2006(2):48-51.
[6]魏芳斌.输电线路子导线粘连原因分析[J].福建电力与电工,2006,26(1):38-39.Wei Fangbing.Cause analysis of vertical-arrayed double-bundled transmission line conglutination[J].Fujian Electric Power and Electrical Engineering,2006,26(1):38-39.
[7]杨高光辉.220kV 垂直双分裂导线粘连原因及整改措施[J].湖南电力,2009,29(5):42-44.Yang Gao-guanghui.Cause analysis for 220kV vertical arrangement twin bundled lines Conglutination and countermeasures[J].Hunan Electric Power,2009,29(5):42-44.
[8]姚耀明.220kV 垂直排列双分裂导线粘连的分析与研究[J].浙江电力,2006(6):49-52.Yao Yaoming.Analysis on conglutination phenomena of vertical-arrayed double-bundled transmission line of 220kV[J].Zhejiang Electric Power,2006(6):49-52.
[9]包建强.220kV 架空输电线路相双分裂垂直排列导线粘连原因分析及技术防范措施[J].电力设备,2009,9(5):76-78.Bao Jianqiang.Case study and technical countermeas-ures of conglutination with double phases for 220 kV vertical-arrayed twin-bundled transmission line overhead transmission line[J].Electrical Equipment,2009,9(5):76-78.
[10]潘基书,陈杰.垂直双分裂导线粘连原因分析[J].云南电力技术,2007,35(3):30-32.Pan Jishu,Chen Jie.Cause analysis of vertical twin bundled line conglutination[J].Yunnan Electric Power,2007,35(3):30-32.
[11]胡江涛.220kV 小四甲乙线路垂直双分裂子导线粘结问题的分析及解决方案[J].宁夏电力,2007(3):19-21.Hu Jiangtao.Analysis and solving schemes for conglutination of 220kv vertical-arrayed double-bundled transmission line Xiaosijiayi[J].Ningxia Electric Power,2007(3):19-21.
[12]姜海波,叶勇.双分裂输电线路导线粘连成因及处理方法[J].江苏电机工程,2007,26(4):49-51.Jiang Haibo,Ye Yong.Cause analysis and disposal of twin bundled line conglutination[J].Jiangsu Electrical Engineering,2007,26(4):49-51.
[13]沈亚红.架空输电线路双分裂导线粘连原因及维护方法[J].江西电力职业技术学院学报,2008,21(3):35-37.Shen Yahong.Causes analysis and disposal of vertical-arrayed double-bundled transmission line conglutination[J].Journal of Jiangxi Vocational and Technical College of Electricity,2008,21(3):35-37.
[14]樊灵孟.220kV 垂直排列双分裂导线粘连现象分析[J].高电压技术,2004,30(6):27-29.Fan Lingmeng.Analyses on conglutination phenomena of 220kV vertical-arrayed double-bundled transmi-ssion-lines[J].High Voltage Engineering,2004,30(6):27-29.
[15]罗锋.双分裂导线粘连问题的分析与处理[J].广东科技,2008(12):134-136.Luo Feng.Analysis of transmission twin conductor bundle conglutination[J].Guangdong Electric Power,2008(12):134-136.
[16]E D Charles.Mechanical forces on current-carrying conductors[J].Proceedings of the IEE,1963,110(9):1671-1677.
[17]P R Mehta,R L Swart.Generalized formulation for electromagnetic forces on current-carrying conductors[J].IEEE Transactions on Power Apparatus And Systems,1967,86(2):155-165.
[18]李博之.高压架空输电线路架线施工计算原理[M].北京:中国电力出版社,2008.
[19]黄向平.输电线路架空线水平应力方程解的探讨[J].水利科技,2002(1):60-61.Huang Xiangping.Discuss on solution of aerial transmission lines level stress equation[J].Hydraulic Science and Technology,2002(1):60-61.
[20]吕永乐.孤立档架空导线应力与弧垂计算分析[J].甘肃科技,2008,24(13):58-60.Lü Yongle.The stress and sag calculated of overhead conductor in isolated span[J].Gansu Science and Technology,2008,24(13):58-60.
[21]韦世平.导线应力状态方程新解法[J].上海电力,2000(2):50-51.Wei Shiping.New solution of state equation of lead stress[J].Shanghai Electric Power,2000(2):50-51.
[22]张三慧.电磁学[M].北京:清华大学出版社,2003.
