基于多时段同步测量信息的T接线路参数在线测量
2012-07-06牛胜锁梁志瑞张建华苏海锋
牛胜锁 梁志瑞 张建华 苏海锋
(华北电力大学新能源电力系统国家重点实验室 保定 071003)
1 引言
线路参数通常采用设计值或经验值。由于部分线路的设计运行条件与实际运行条件之间存在差别,且元件自身也在局部、缓慢地变化,因此线路参数的设计值与真实值之间可能存在较大的差值。电力系统状态估计、潮流计算、网损分析和继电保护整定计算等都要求线路参数足够准确,因此,提高线路参数测量的准确性对电网的安全稳定运行具有重大意义。
随着广域测量系统(Wide Area Measurement System,WAMS)在电力系统应用越来越广泛,基于线路两端同步测量信息的线路参数在线测量取得了一定发展[1-4],另外,一些具有同步测量功能的电能质量监测系统及便携式可灵活组网的广域测量系统[5]的应用,也为线路参数的在线测量提供了条件。目前,相关研究工作主要集中在基于线路双端同步信息的参数测量[6-10],而对含有T 接的线路,因T接点的电压及电流不能直接测量,未有有效算法可进行测量。本文基于不同负荷时段的同步测量信息,对T 接线的线路正序参数进行在线测量,推导了相应理论算法。并且推导了一种分析精度较高的加窗插值傅里叶算法,将其应用于同步采样数据的分析,克服了在电网频率发生波动时由于固定采样频率导致的频谱泄漏问题[11-15],提高了线路参数在线测量的准确度。
2 T 接线路参数在线测量理论算法
关于线路的等效电路,当长度较长(>300km)时,一般采用均匀分布参数电路,而对于中等长度线路(100~300km)和短线路(<100km),一般采用集中参数电路[16]。有T 接的线路其各段线路长度一般不会太长,因此采用集中参数电路,分中等长度线路和短线路两种情况进行线路参数测量算法的推导。
2.1 中等长度线路
对于中等长度线路,各段线路模型采用π形等效电路。T 接线路模型等效电路如图1 所示。

图1 T接线路等效电路Fig.1 Equivalent circuit of T-connection transmission line

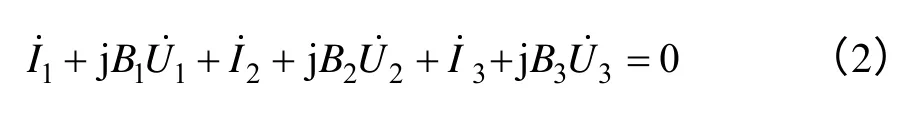
由其他2 时段同步数据可得类同方程,由此可得如下方程组(3 个潮流时段的选择需保证方程满秩):

因式(1)做了近似处理,因此,解方程组(3)可得B1、B2和B3的初次近似解,记为:和。


由式(1)得式(3)的准确表达式为

将求得的各支路参数初次解代入式(4)得

利用测得的同步信息,通过以上两次迭代求解,得到的T 形接线各个参数值具有较高的准确度。
2.2 短线路
对于短线路,一般可忽略线路的电纳B,式(5)变为

求解式(8)线性方程组即可得各段线路的Z参数。
经仿真验证,当测量数据准确时,经过二次迭代得到的线路参数具有很高的准确度。实际中,电网频率总是在一定范围内波动。PMU 为了保证异地采样的同步性一般按某一固定频率采样,从而在利用FFT 分析数据时易造成数据的非整周期截断,进而产生频谱泄漏和栅栏效应,对最终参数测量结果带来较大误差。为了解决该问题,本文推导了一种加窗插值FFT 算法。
3 基于加窗插值FFT的采样数据分析
利用加窗插值FFT 算法可以较好地解决由于数据的非整周期截断产生的频谱泄漏现象。为降低频谱泄漏对信号分析带来的误差,应选择旁瓣峰值电平小且旁瓣渐近衰减速率大的窗函数对信号进行处理。本文选择的4 项5 阶Nuttall[17]窗其时域表示为

式中,a0=10/32,a1=15/32,a2=6/32,a3=1/32;n=0,1,…,N-1。
该窗函数的旁瓣峰值为-60.95 dB,旁瓣渐近衰减速率为42dB/oct,该窗在保证较大的旁瓣衰减速率的同时,有较小的旁瓣峰值,适合用于信号分析。
以单一频率信号为例进行分析,设x(t)以采样频率fs均匀采样得到的离散时域信号为

式中,A1、f1、φ1分别为信号的幅值、频率和初相位,n=0,1,…,N-1,N为采样点数。
对x(n)加4 项5 阶Nuttall 窗得到

加窗序列xw(n)的离散傅里叶变换为

式中,k=0,1,…,N-1,Δf=fs/N,忽略负频点处频峰的旁瓣影响,得到加窗信号的离散傅里叶变换表达式为

式中,W(k)为窗函数的离散傅里叶变换,表达式为

考虑到N≫1,式(13)可近似表示为

对信号非同步采样时,信号的频率kΔf很难正好位于抽样频点上,即k一般不是整数。设在峰值频点附近抽样得到的幅值最大谱线为ka,其左边谱线为ka-1,右边谱线为ka+1,记δ=k-ka,则有-0.5<δ<0.5。准确地求得δ是求解问题的关键,而δ的大小与ka-1、ka和ka+1三条谱线的幅值|X(ka-1)|、|X(ka)|和|X(ka+1)|密切相关,记

由式(12)和式(14)可得

由式(14)和式(16)可得α=(δ+4)/(4-δ),经变形整理可得

通过式(15)和式(17)求得δ后,可求得信号频率

信号的幅值和相位也可通过关于δ的修正函数求得,由式(12)和式(14)可得

相位的修正公式可表示为

为了验证以上插值FFT 算法的有效性,采用文献[15]给出的信号模型进行仿真实验,该信号无噪声离散信号的表达式为
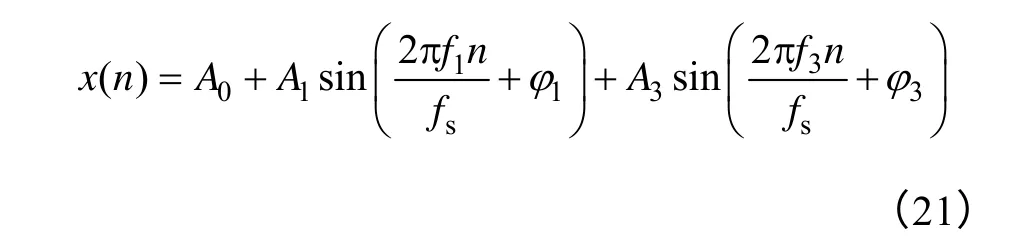
式中,n=0,1,…,N-1,各参数取值为:A0=0.2,A1=6,f1=20.2,φ1=0.1,A3=1,f3=60.6,φ3=0。
式(21)已被众多文献用来验证算法的有效性。本文取:fs=1 000Hz,N=256。在Matlab 环境下仿真,本文算法与加矩形窗[14]、Hanning 窗[14]、Blackman-harris 窗[15]双谱线插值FFT 进行对比,各算法计算结果的绝对误差见表1。表1 仿真结果表明,本文算法相对于经典加窗插值FFT 算法有更高的分析精度,用于线路参数的在线测量可获得更好的效果。
4 仿真验证
4.1 电网频率变动对算法的影响
在Matlab 环境下搭建如图1 所示的含T 形接线的三相电路模型,在节点1 加电源,在节点2 和节点3 加负荷,电压等级取为110kV,测量数据和线路参数取标幺值,UB=110kV,SB=100MVA,各支路参数取值见表2。

表1 不同加窗插值FFT 算法结果的误差比较Tab.1 Comparison of simulation results using different window interpolation FFT algorithms

表2 仿真电路中各参数的真值Tab.2 Truth-values of the artificial circuit parameter
通过改变节点2 和节点3 负荷的大小,得到3种不同潮流时段的离散同步采样数据。对信号的采样频率取10kHz,数据长度取2 000 点,对采样数据利用第3 节所述加窗插值FFT 算法进行分析,得到三相基波电压、电流相量,用对称分量法求得正序分量,按第2 节方法计算T 接线路参数。电网频率在49.50~50.50Hz 变动时各参数测量结果的相对误差见表3。

表3 不同电网频率下测量结果的相对误差Tab.3 Relative error of measurement under different frequency
从表3 数据可以看出,当电网频率在49.5~50.5Hz 变动时,线路参数测量都具有较高的准确度,电阻的测量误差相对较大,但其最大误差也小于0.15%。
4.2 白噪声对算法的影响
在实际测量中,测得的数据都是含有白噪声的。为了验证算法在采样数据含有白噪声情况下的有效性,进行了仿真,模型同前,电网频率取50.50Hz,对测量的三相电压和电流离散采样信号加入高斯白噪声,不同信噪比下线路参数测量结果相对误差以第1 段线路为例列出,结果见表4。

表4 不同信噪比下测量结果的相对误差Tab.4 Relative error of measurement under different SNR
由表4 数据可以看出,信噪比较低(<50dB)时,各参数测量误差均较大。当信噪比大于60dB时,R和X的测量误差均小于0.5%,而B的测量准确度受信噪比影响较大,但在信噪比大于60dB 时其误差小于5%。
5 现场实际运行
利用研制的广域测量系统对河北南网一处含T接线路进行了在线测量,线路示意图如图2 所示,支路1 为220 kV 变电站的一条出线,支路2 和支路3 分别为2 座110 kV 变电站的进线,各段线路型号及长度标于图3 中。线路参数的设计值见表5。

图2 被测的T 接线示意图Fig.2 Schematic diagram of the measured T-connection line

表5 T 接线参数设计值Tab.5 Design values of the T-connection line parameters
便携式PMU 安装于3 个变电站,进行了一段时间的同步测量。PMU 每隔5min 进行一次同步采样,并将数据通过GPRS 无线网络传送至数据处理中心。监测完成后由数据处理中心自动筛选负荷差异较大时段的同步采样数据,进行线路参数的计算,因线路长度较短,忽略B参数,若干次测量结果及其平均值见表6。

表6 T 接线参数实测结果Tab.6 Measurement results of the T-connection line parameters
通过实际测量发现,单次测量值在一定范围内波动,尤其是电阻值较小的R2和R3波动相对较大,通过求平均值可获得相对较为稳定的测量结果,因此,取其平均值作为最终测量值。
通过对比在线测量值和设计值发现,两者存在一定差别,电阻相差约在6%~10%,电抗相差约在2%~5%。分析其原因,在于两个方面:①随着线路的运行老化及环境的变化,设计值偏离其真实值;②由于系统PT、CT的误差及PMU的测量误差,导致在线测量值与真实值之间存在差别。
为了比较参数在线测量值和设计值哪个更接近真实值,利用SCADA 系统提供的数据进行验证,由SCADA 系统获取的与T 接线3 端相关的视在功率S(注入母线为正)和线电压U的一组数据见表7。

表7 T 接线相关的SCADA 数据Tab.7 Data of T-connection line obtained from SCADA
根据节点2 和节点3的SCADA 数据分别利用线路的设计参数和实测参数计算节点1的U和S,与SCADA 系统提供的节点1的U和S对比。利用线路设计参数计算得到的节点1的线电压、有功和无功量与 SCADA 提供的对应值之差为:ΔU1=0.35kV,ΔP1=346kW,ΔQ1=203kvar;利用线路实测参数计算得到的节点1的线电压、有功和无功量与SCADA 提供的对应值之差为:ΔU1=0.21kV,ΔP1=318kW,ΔQ1=159kVar。由此可见,线路参数取在线测量值时,3 个变电站SCADA 数据的吻合度比线路参数取设计值要好,验证了在线测量值的准确可靠。
6 结论
本文提出的利用含T 接输电线路三端多时段同步测量信息进参数在线测量的方法,经过了河北南网110 kV 含T 接线路正序参数带电测量的检验,证明方法是正确可行的,测量结果能够满足工程要求。
本文所提方法对三绕组变压器及其他电力系统元件参数的在线测量也有一定借鉴意义。
[1]陈允平,张承学,胡志坚.以 GPS 为基础的线路参数带电测量[J].电力系统自动化,1998,22(6):43-45.Chen Yunping,Zhang Chengxue,Hu Zhijian.Zero-sequence parameter measurement under operation of transmission line with mutual inductance based on GPS technology[J].Automation of Electric Power Systems,1998,22(6):43-45.
[2]Borda C,Olarte A,Diaz H.PMU-based line and transformer parameter estimation[C].2009 IEEE Power Systems Conference and Exposition(PSCE2009),Seattle,Washington,USA,2009:1-8.
[3]王茂海,鲍捷,齐霞,等.基于PMU 实测数据的输电线路参数在线估计方法[J].电力系统自动化,2010,34(1):25-27,31.Wang Maohai,Bao Jie,Qi Xia,et al.Online estimation of transmission line parameters based on PMU measurements[J].Automation of Electric Power Systems,2010,34(1):25-27,31.
[4]于淼.基于同步相量测量技术的线路参数在线辨识[D].天津:天津大学,2005.
[5]Liang Zhirui,Niu Shengsuo,Su Haifeng,et al.Research of flexible wide-area measurement and analysis system in power system[C].2010 International Conference on Electricity Distribution(CICED 2010),Nanjing,China,2010:1-4.
[6]柴京慧,李书敏,何桦.基于PMU 及多时间断面的输电网参数估计[J].电力系统自动化,2009,33(11):49-52.Chai Jinghui,Li Shumin,He Hua.Parameter estimation based on PMU and multi-cases of SCADA for electricity transmission network[J].Automation of Electric Power Systems,2009,33(11):49-52.
[7]李钦,项凤雏,颜伟,等.基于SCADA 及PMU 多时段量测信息的独立线路参数估计方法[J].电网技术,2011,35(2):105-109.Li Qin,Xiang Fengchu,Yan Wei,et al.An approach to estimate parameters of single transmission line based on multi-interval information measured by SCADA and phasor measurement units[J].Power System Technology,2011,35(2):105-109.
[8]李澍森,陈晓燕,吴彦皎,等.多回平行输电线路参数带电测量[J].电力系统自动化,2009,33(22):84-87,97.Li Shusen,Chen Xiaoyan,Wu Yanjiao,et al.Live line measurement of several parallel transmission lines[J].Automation of Electric Power Systems,2009,33(22):84-87,97.
[9]胡志坚,陈允平,徐玮,等.基于微分方程的互感线路参数带电测量研究与实现[J].中国电机工程学报,2005,25(2):28-33.Hu Zhijian,Chen Yunping,Xu Wei,et al.Principles and realization of live line measurement of parameters of transmission lines with mutual inductance based on differential equations[J].Proceedings of the CSEE,2005,25(2):28-33.
[10]Yuan Liao,Kezunovic.Online optimal transmission line parameter estimation for relaying applications[J].IEEE Transactions on Power Delivery,2009,24(1):96-102.
[11]Andria G,Savino M,Trotta A.Windows and interpolation algorithms to improve electric measurement accuracy[J].IEEE Transactions on Instrumentation and Measurement,1989,38(8):856-863.
[12]Jain Vijay K,Collins Willim L.High-accuracy analog measurements via interpolated FFT[J].IEEE Transactions on Instrumentation and Measurement,1979,28(2):113-122.
[13]潘文,钱俞寿,周鹗.基于加窗插值FFT的电力谐波测量理论(Ⅱ)—双插值FFT 理论[J].电工技术学报,1994,9(2):53-56.Pan Wen,Qian Yushou,Zhou E.Power harmonies measurement based on windows and interpolated FFT(Ⅱ)—dual interpolated FFT algorithms[J].Transactions of China Electrotechnical Society,1994,9(2):53-56.
[14]庞浩,李东霞,俎云霄,等.应用 FFT 进行电力系统谐波分析的改进算法[J].中国电机工程学报,2003,23(6):49-54.Pang Hao,Li Dongxia,Zu Yunxiao,et al.An improved algorithm for harmonic analysis of power system using FFT technique[J].Proceedings of the CSEE,2003,23(6):49-54.
[15]许珉,张鸿博.基于Blackman-harris 窗的加窗FFT 插值修正算法[J].郑州大学学报(工学版),2005,26(4):99-101.Xu Min,Zhang Hongbo.The correction algorithm based on the Blackman-harris windows and interpolated FFT[J].Journal of Zhengzhou University(Engineering Science),2005,26(4):99-101.
[16]陈珩.电力系统稳态分析[M].北京:中国电力出版社,2007.
[17]Nuttall A H.Some windows with a very good sidelobe behavior[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1981,29(1):84-91.
