基于液流电池储能的光伏发电系统容量配置及成本分析
2012-07-06胡国珍段善旭陈昌松
胡国珍 段善旭 蔡 涛 陈昌松
(1.华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074 2.湖北理工学院电气学院 黄石 435003)
1 引言
光伏发电容易受气候、环境等因素的影响,其输出具有随机性和不稳定性,为提高供电质量,保障供电可靠性,在设计光伏发电系统时必须考虑能量储能单元的配置[1,2]。
光伏发电系统或混合发电系统通常采用铅酸蓄电池(Lead-Acid Batteries,LAB)作为储能单元,但由于铅酸蓄电池存在充放电周期长、寿命短以及环境污染等问题,使其在可再生能源发电系统中推广应用受到较大限制。如在光伏发电系统中,通常采用的能量管理策略是将多余的能量存储在蓄电池中,常规充电方法使蓄电池充满须耗时5~6h,而通常能量过剩只出现在正午光伏发电输出功率峰值时,峰值时间仅持续约2~3h,因而采用铅酸蓄电池作为储能单元使光伏发电功率无法得到有效利用。相关机构已展开其他储能方式应用在光伏发电系统中的研究,文献[3]研究了燃料电池配合电解液储能在混合发电系统中的应用,但燃料电池动态响应较慢,且容量/价格比较低,增加了系统运行成本。文献[4]提出将超级电容应用于光伏发电系统中,但超级电容存在体积过大、若使用不当极易造成电解液泄露等缺点。
全钒液流电池(Vanadium Redox Batteries,VRB)是一种新的能量储能电池,其具有能量效率高、蓄电容量大、使用寿命长、循环寿命高、超深度放电不引起电池的不可逆损伤、电池部件材料性能稳定、易于回收以及系统运行安全和环境友好等特点[5,6],因此其可应用在可再生能源发电系统中,且可作为长期储能单元。目前针对液流电池的研究主要集中在电化学特性方面,将其应用在可再生能源发电系统中的研究较少。文献[7,8]提出将全钒液流电池应用于光伏发电系统中,主要侧重于研究全钒液流电池特性。文献[9,10]基于仿真分析研究了液流电池用于风力发电系统中,用于平抑风力发电波动。以上文献对全钒液流电池与可再生能源(风、光)的容量配置、运行经济性评估以及能量管理等问题均考虑甚少,但随着全钒液流电池的推广应用,业内已开始关注这些问题。
合理的容量配置是保证光伏发电系统供电可靠性的一个重要因素,在独立光伏发电系统中,通常采用的方法是依靠满足负荷需求的自治天数,系统供电可靠性完全取决于储能容量的大小。这种方法未考虑光伏输出功率、储能单元以及负荷之间的能量交换关系,只考虑极限天气条件下的自治天数,因此也不存在容量优化问题。本文采用一种基于负荷缺电率(Loss of Power Supply Probability,LPSP)指标来衡量供电可靠性的容量配置方法[11],重点研究全钒液流电池应用于独立光伏发电系统中的容量配置问题,同时与铅酸蓄电池进行了比较分析。在此基础上,从经济性角度分析了系统单位运行成本,并以系统成本最小化为目标对系统容量进行了优化配置。这种方法既权衡了光伏发电的波动和负荷的变化,又考虑了光伏发电单元与储能单元之间的能量管理。
2 光伏发电系统建模

图1 光伏发电系统Fig.1 PV generation system
如图1 所示,带储能单元的光伏发电系统主要由光伏阵列、储能单元和负荷3 个单元以及相应变换器组成,能量流动在这3 个单元间进行。DC-DC 变换器C1 主要用于提升光伏组件输出电压,同时完成最大功率跟踪(MPPT)功能;C2为双向DC-DC 变换器,用于维持直流母线电压恒定以及对储能单元进行充放电控制;DC-AC 逆变器C3 用于将直流电能变换为负荷需求的相应频率和电压等级的交流电能。容量配置主要针对系统能量流进行管理,下文建立了光伏发电单元和储能单元的功率模型。
2.1 光伏发电单元建模
光伏发电的输出具有随机性,其组件的输出功率受辐照度、组件光照面积、光电转换效率以及温度的影响,其输出功率可表示为
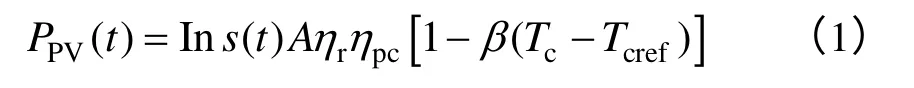
式中,ηr为组件光电转换效率;β为温度系数;Tc为环境温度;Tcref为环境参考温度;ηpc为直流变换环节MPPT 效率;Ins(t)为辐照度,W/m2;A为光伏组件面积。
2.2 全钒液流电池建模
全钒液流储能电池是一种电能储存装置,主要由电池模块、电解质溶液和电解质溶液储存输送体系以及能量管理控制系统等组成[12]。

全钒液流电池容量与功率独立设计,能量由活性化学物质和溶液罐容积决定,功率由电极板面积和电池尺寸决定。其输出电压主要受温度、荷电状态等因素影响,输出方程为 式中,Vcell为单体电池输出电压;Vequ为电极等效电动势;R为极间等效电阻;T为电池工作温度;F为法拉第常数;SOC为荷电状态。全钒液流电池损耗Ppara主要由固定损耗Pflxed(电极板腐蚀而产生的损耗)和溶液泵损耗两部分组成。
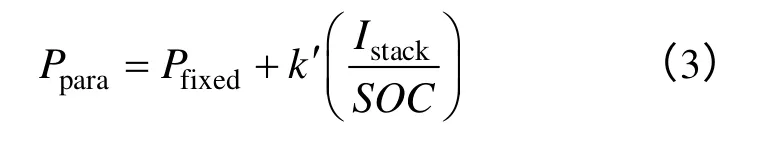
式中,Istack为极间电流;k′为损耗系数。因此,由式(2)和式(3)可得出液流电池输出功率为

2.3 铅酸蓄电池建模
目前相关文献已建立了多种铅酸蓄电池模型,常规模型中电池容量可表示为

式中,LABC为铅酸蓄电池实际容量;为铅酸蓄电池额定容量;δc为铅酸蓄电池温度系数,通常取δc=0.6%;TLAB为实际工作温度。
3 容量配置方法
光伏发电系统与储能单元容量配置目标是为满足在一定负荷条件下,系统能量的供需平衡。一定时间内光伏发电系统产生能量W可表示为

式中,P(t)为一定时间序列n下系统输出功率。容量配置方法主要是对储能单元的能量管理。当负荷需求功率Pload(t)大于光伏发电功率Pgen(t)时,储能单元通过C2 释放能量以满足系统能量差值,一定时间内储能单元能量为
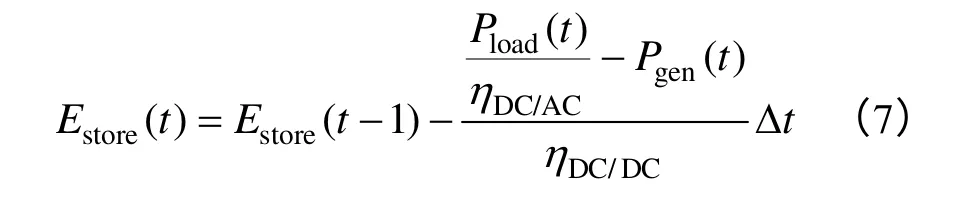
当负荷功率需求小于光伏发电功率时,光伏发电系统多余能量供给蓄电池,通过C2 向蓄电池充电,一定时间内储能单元能量为

式中,ηDC/AC为变换器C3 效率;ηDC/DC为变换器C2 效率。
本文采用负荷缺电率(LPSP)指标来确定储能单元容量配置。负荷缺电率表示一定时间内光伏发电系统不能满足负荷功率需求的概率。单位时间内负荷能量欠缺可表示为

由于负荷能量欠缺为正的量纲,因此分析时取LPS(t)≥0,满足供电要求时LPS(t)=0。
负荷缺电率函数定义为

LPSP依据用户负荷和当地电网要求进行取值,LPSP=0 表示系统在一定运行时间内发电功率能有效满足负荷需求,LPSP=1 则表示系统发电功率无法满足负荷需求。
4 系统运行成本组成
系统运行经济性主要通过其单位成本LCE分析来体现。LCE分析主要考虑初始安装成本、维护费用、置换成本等因素,定义LCE

式中,Cm为运行总成本;CRF为资本回收周期;Egen为年发电量。运行成本和资本回收周期可由式(12)和式(13)计算

式中,r为资本折旧率;Cinit为初始安装成本;Cmaintance为维护成本;Creplace为置换成本。
铅酸蓄电池与全钒液流电池的结构和制造工艺的差异性决定了其成本组成不同。铅酸蓄电池结构简单,其电极和电解液为一体,不含控制系统,费用固定,更换时须一次性全部更换。而全钒液流电池功率和容量分开设计,其费用主要由电极、电解液、循环泵、控制系统等组成,更换时须更换电解液和泵等部件。全钒液流电池初始成本Ccapital可定义为[13]
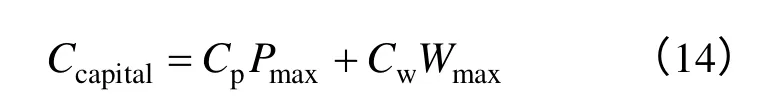
式中,Cp为储能单元单位功率运行成本;Cw为储能单元单位容量运行成本;Pmax为储能单元输出最大功率;Wmax为储能单元输出最大容量。根据铅酸蓄电池结构,Cp为0,因此其初始成本组成可简化为

5 系统容量配置分析
传统铅酸蓄电池与液流电池在工作特性上有显著差异,使其应用在光伏发电系统中有较大区别,两种储能单元在进行容量配置上的差异主要体现在放电深度(DOD)、自放电率以及充放电效率上,见表1。表1 给出了全钒液流电池和铅酸蓄电池容量配置算法中的相关参数[9]。为体现差异性,式(7)和式(8)可修正为

约束条件

式中,δ为储能单元自放电率;ηmd为变换器效率C2 与储能单元放电效率乘积;ηmc为变换器效率C2与储能单元充电效率乘积;SOCmax为最大可利用荷电状态。

表1 两种电池参数差异Tab.1 Difference of these two kinds of batteries
储能单元SOC随系统充放电变化而变化,主要与电池初始状态、充放电电流和充放电时间有关。考虑这些因素,某一时刻t+1 储能单元SOC可表示为

式中,ηbat为电池充放电效率;Vbat为电池端电压;Ibat为电池充放电电流,可表示为

以华中地区某一光伏电站为例,结合该电站相关统计数据进行系统容量配置分析。图2 所示为华中地区(东经114°,北纬30°)年辐照度分布曲线,图3 为该电站典型用户日负荷曲线,这里假定年负荷曲线保持相同。图4 为该地区月平均温度曲线。

图2 年辐照度Fig.2 Hourly average radiation

图3 日负荷曲线Fig.3 Daily average demand of a typical residence
图4 月平均温度曲线Fig.4 Monthly average temperature
根据统计数据,以小时为单位按一年8 760h 来计算光伏发电单元的发电功率,同时结合负荷情况采用修正后的容量配置方式(见式(16))计算储能单元应发出或吸收的储能容量;然后根据不同时刻的光伏发电功率,以固定步长配置满足一定约束条件下不同容量的储能单元,最后以公式(10)计算不同配置下的负荷缺电率LPSP,从而可得出光伏发电功率和储能单元能量匹配关系。这里针对铅酸蓄电池和全钒液流电池进行对比分析。图5 为采用铅酸蓄电池作为储能单元的光伏发电系统容量配置关系曲线,其中ELAB为铅酸蓄电池配置容量;图6 为采用全钒液流电池作为储能单元的光伏发电系统容量配置关系曲线,其中EVRB为液流电池配置容量。
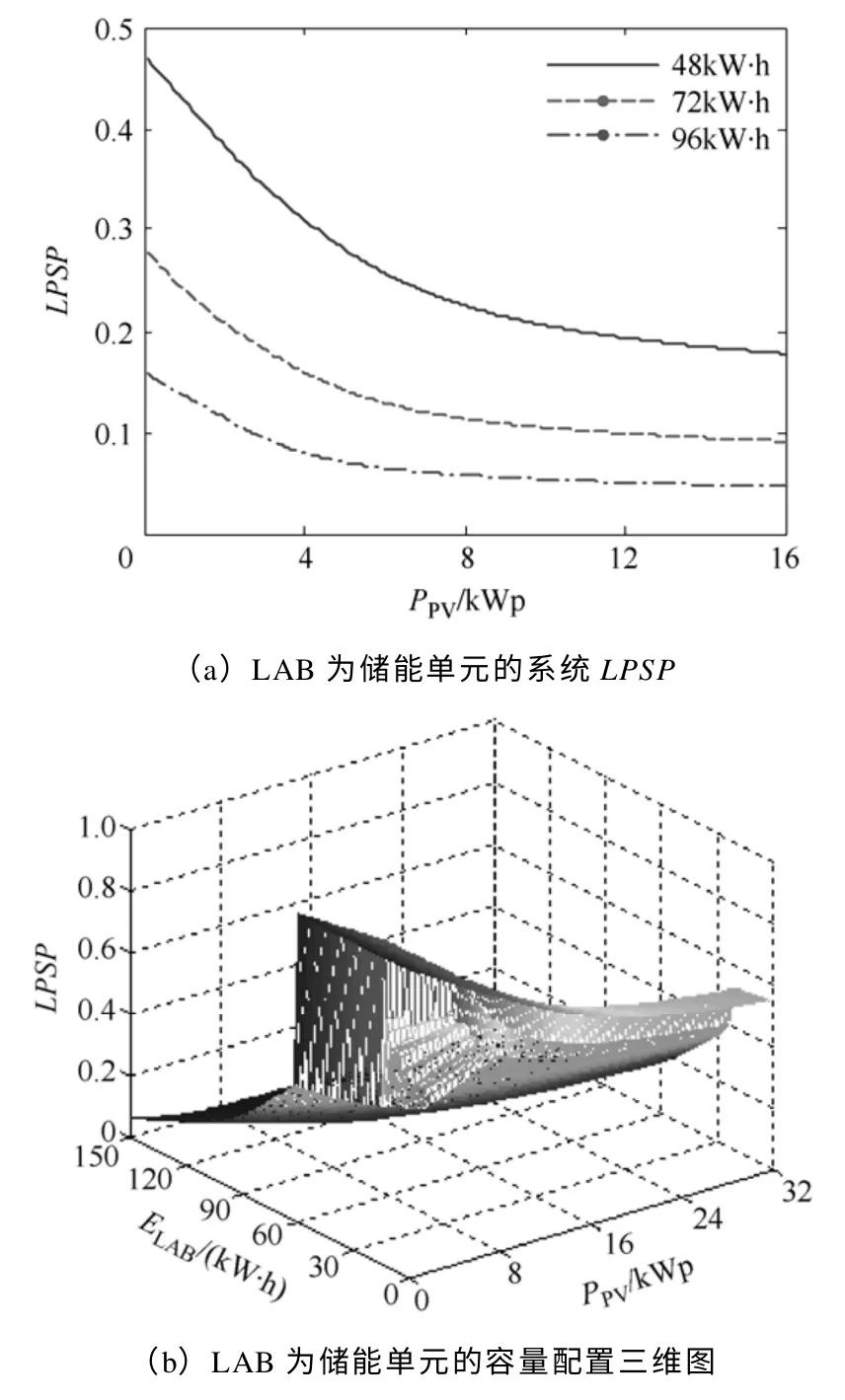
图5 LAB 为储能单元的系统容量配置Fig.5 Sizing combination of PV system with LAB

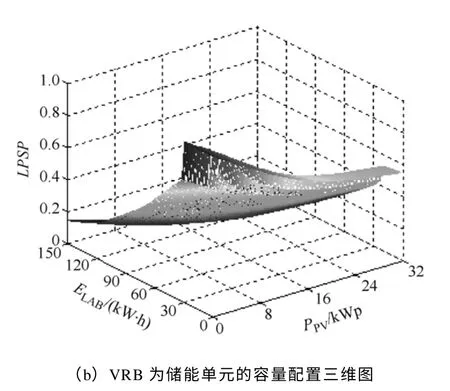
图6 VRB 为储能单元的系统容量配置Fig.6 Sizing combination of PV system with VRB
由图5 和图6 可看出,在一定负载条件下,系统配置光伏组件容量越大,所需储能单元越小,同时相应的LPSP也就越小。在储能单元和光伏组件容量确定的条件下,采用液流电池作为储能单元,系统LPSP较低,供电可靠性高。例如在光伏组件输出功率为12kW的情况下,以全钒液流电池作为储能单元,配置储能容量为72kW·h(约两天储能容量)时,系统LPSP为0.1,当储能容量增加到96kW·h时,系统LPSP可提高到0.025。而如果采用铅酸蓄电池作为储能单元,配置72kW·h 和96kW·h的储能容量,系统LPSP分别为0.15 和0.08。这种差异主要是由于两种储能单元性能参数的差异而导致实际供能不同造成的。在保持相同LPSP和储能单元容量条件下,相对于铅酸蓄电池,采用液流电池作为储能单元可减小光伏组件容量配置。从图中也可看出,增大储能单元容量对提高系统供电可靠性的作用明显优于增大光伏组件容量。
6 成本分析及优化配置
6.1 额定光伏容量成本分析
根据第5 节介绍的全钒液流电池与铅酸蓄电池成本构成的差异性,表2 给出了两者相关费用[14]。铅酸蓄电池超出工作寿命则直接替换,因此在其工作寿命之内其置换成本为零,而全钒液流电池在其工作寿命之内还须考虑由于泵损耗而造成的置换费用。取年利率r=5%,根据系统各组件运行寿命可得出全钒液流电池、铅酸蓄电池的资本回收因子分别为0.080 2 和0.231。

表2 两种电池运行费用Tab.2 Operation capital of VRB and LAB
结合表1、表2 进行仿真,图7 给出了不同容量下光伏发电系统单位成本。
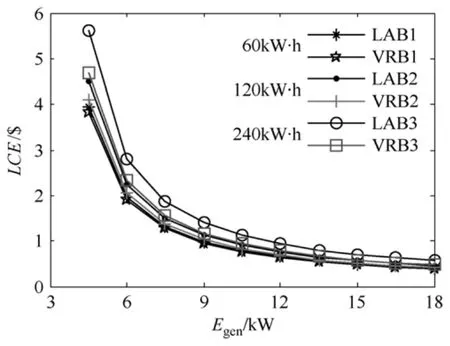
图7 不同容量配置下光伏发电系统LCEFig.7 LCE of PV system with different sizing combinations
表3 对额定光伏发电容量(18kW)下配置不同容量铅酸蓄电池和全钒液流电池单位费用进行了比较。
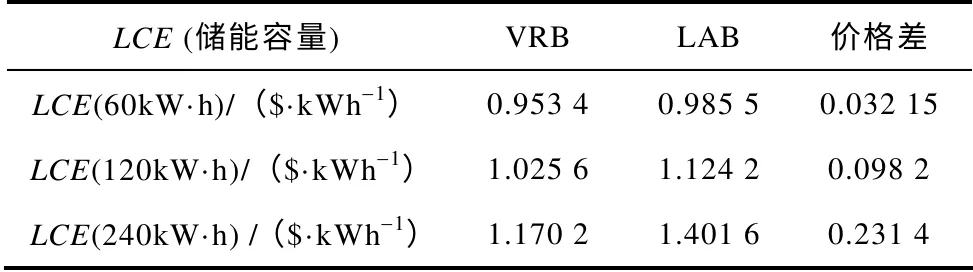
表3 额定光伏容量下不同储能容量单位成本 Tab.3 LCE of different storage combination for a desired PV sizing
由表3 可看出在一定负荷条件下配置相同容量的全钒液流电池的光伏发电系统单位成本花费低于相应容量的蓄电池发电系统,配置储能单元容量越大,采用全钒液流电池作为储能单元的系统单位运行成本花费优势越明显。但由于液流电池功率和容量分开设计,功率部分占据了一定的固定费用,在低容量配置情况下液流电池并不占优势,图8 给出了光伏额定功率为18kW 不同容量配置下两种储能单元单位成本费用的差异。从图8 可看出,当配置储能容量较低时即在光伏额定功率为18kW 时配置储能容量低于30kW·h,采用液流电池储能单位成本费用较高,实际分析中可知,过低的储能单元容量会使系统可靠性较差,且不能满足此时的负荷条件下要求。根据前述成本分析方法也可进一步计算分析不同光伏功率等级和负荷条件下的单位成本费用,相对于铅酸电池储能,采用液流电池储能,配置储能容量越大,系统单位运行成本越低,经济性越明显,由此可看出液流电池储能在规模化储能方面具有优势。

图8 两种储能单元单位费用比较Fig.8 LCE comparison of these two energy storage
可进一步分析在额定光伏发电容量下满足一定LPSP要求(LPSP=0.1)的容量配置及单位成本花费,见表4。
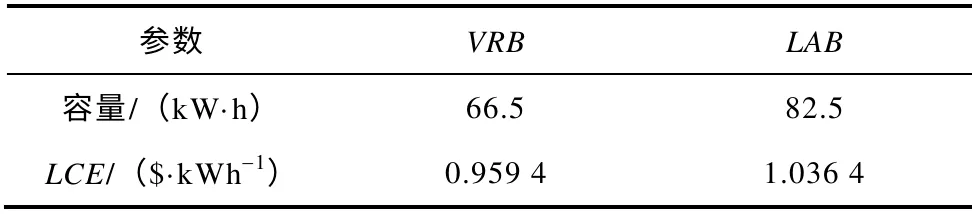
表4 额定光伏容量配置(LPSP=0.1)及成本Tab.4 LCE for a desired PV sizing(LPSP=0.1)
由以上分析可看出,额定光伏发电容量下,采用液流电池作为储能单元,在满足一定负荷条件下,其单位运行费用低于铅酸蓄电池,应用在光伏发电系统中具有较好的经济性。
6.2 优化配置
在实际容量配置中,设计和优化光伏组件容量和储能单元容量配置必须综合考虑负荷、光照以及系统负荷缺电率等因素,才能使系统具有较好的经济性,上节主要分析了额定光伏容量下的光伏发电系统的容量配置,此种配置从经济角度考虑并非最优。为最优化系统配置,以经济性为目标,结合式(14),可定义基于液流电池储能的光伏发电系统经济目标函数如下

式中,Csys为系统总成本;Csm为储能单元容量;CPV为光伏发电单元容量;Closs为系统总损耗;γ为液流电池功率等级;δPV为光伏发电单元单位成本。系统优化目标为单位时间内总成本最小,这里假定系统总损耗为固定值。由第5 节分析可知,一定LPSP条件下,光伏组件成本和储能单元成本互为单调关系,即随着光伏组件容量增加(减小)储能单元容量减小(增大),因此针对系统总成本寻优可考虑为 单极值点求解问题,满足:,可得到最优容量配置,即在系统总损耗一定的情况下,系统满足
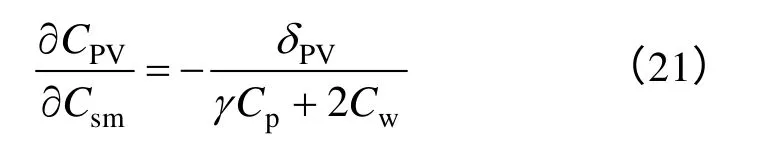
可获得系统运行最小成本。
根据以上优化配置原理,假定满足系统LPSP为0.1的条件下,对系统进行优化配置,图9 给出了采用全钒液流电池作为储能单元的优化配置曲线。图中切线斜率为,与曲线相交点即为满足系统总运行费用最小的工作点。

图9 光伏发电系统优化配置Fig.9 Optimal sizing of PV system with VRB
由图9 可知,满足一定LPSP(0.1)和负荷(图3 所示)情况下,采用全钒液流电池(γ=10kW)的光伏发电系统优化配置容量为15kW/75kW·h,系统单元费用为$0.93,低于额定光伏容量配置下的单位成本费用。
7 结论
采用负荷缺电率指标研究了光伏发电系统容量配置。通过比较全钒液流电池和铅酸蓄电池特性和运行成本差异,分析了两种电池应用于光伏发电系统中的容量配置问题。全钒液流电池因其优越的电池特性,应用在光伏发电系统中具有较好的经济性。本文采用的分析方法可进一步研究扩展到大规模光伏发电领域,为光伏电站建设中的容量配置提供理论依据。
[1]Chiang S J,Chang K T,Yen C Y.Residential photovoltaic energy storage system[J].IEEE Transactions on Industrial Electronics,1998,45(3):385-390.
[2]Carrasco J M,Franquelo L G,Bialasiewicz J T.Power-electronic systems for the grid integration of renewable energy sources:a survey[J].IEEE Transactions on Industrial Electronics,2006,53(4):1002-1016.
[3]Agbossou K,Kolhe M,Hamelin J,et al.Performance of a stand-alone renewable energy system based on energy storage as hydrogen[J].IEEE Transactions on Energy Conversion,2004,19(2):633-640.
[4]Singo T A,Martinez A,Saadate S.Using ultracapacitors to optimize energy storage in a photovoltaic system[C].International Symposium on Power Electronics,Electrical Drives,Automation and Motion,2008:229-234.
[5]Li M H,Funaki T,Hikihara T.A study of output terminal voltage modeling for Redox flow battery based on charge and discharge experiments[C].Power Conversion Conference-Nagoya,2007:221-225.
[6]Rydh C J.Environmental assessment of vanadium redox and lead-acid batteries for stationary energy storage[J].Journal of Power Sources,1999,80(1-2):21-29.
[7]Joerissen L,Garche J,Fabjan Ch,et al.Possible use of vanadium redox-flow batteries for energy storage in small grids and stand-alone photovoltaic systems[J].Journal of Power Sources,2004,127(1-2):98-104.
[8]Fabjan Ch,Garche J,Harrer B,et al.The vanadium redox-battery:an efficient storage unit for photovoltaic systems[J].Electrochemical Acta,2001,47(5):825-831.
[9]Barote L,Weissbach R,Teodorescu R.Stand-alone wind system with vanadium Redox battery energy storage[C].11th International Conference on Optimization of Electrical and Electronic Equipment,2008:407-412.
[10]Lone S A,Mufti Mairaj-ud-Din.Integrating a Redox flow battery system with a wind-diesel power system[C].International Conference on Power Electronics,Drives and Energy Systems,2006:1-6.
[11]Borowy B S,Salameh Z M.Methodology for optimally sizing the combination of a battery bank and PV array in a wind/PV hybrid system[J].IEEE Transactions on Energy Conversion,1996,11(2):367-375.
[12]Chahwan J,Abbey C,Joos G,et al.VRB modelling for the study of output terminal voltages,internal losses and performance[C].IEEE Canada Electrical Power Conference,2007:387-392.
[13]Chacra F A,Bastard P,Fleury G,et al.Impact of energy storage costs on economical performance in a distribution substation[J].IEEE Transactions on Power System,2005,20(2):684-690.
[14]Chacra F A,Bastard P,Fleury G,et al.Energy storage associated to wind farms in a two-tariff structure bidding tender[C].IEEE Russia Power Tech,2005:1-5.
