常利率下的再保险风险模型的破产概率

陈 丽

(重庆大学数学与统计学院，重庆 401331)

风险过程的破产理论是非寿险精算理论研究的一个经典专题，破产概率是度量风险的重要指标，因此对破产概率的研究是保险学中的重要研究课题。破产论的研究源于瑞典精算师Lundberg的博士论文，不过他的工作不符合现代数学的严格标准。最早的经典风险模型是由Cramer于1930年提出的。后来，许多学者通过在经典模型中引入一些对模型有影响的因素，对经典风险模型进行推广。比如利率因素［1-4］、再保险因素［4-7］等。文献［1-7］仅仅考虑了利率或再保险因素对保险公司的单一影响，但实际情况是，保险公司需要考虑利率等许多因素造成的综合影响。因此，本文同时考虑利率和再保险的双重影响，利用递推的方法，结合微分方程得到连续时间风险模型的破产概率表达式及其Lundberg上界，并且给出了在特殊情形下其破产概率的具体表达式。

1 再保险风险模型

首先给出Cramer-Lundberg经典风险模型。定义:索赔时间间隔序列为第n次索赔时刻，并约定T0=0;{Yn，n≥1}为第n次索赔额，N(t)=sup{n:Tn≤t}为到时刻t的总索赔次数。假设:{Xn，n≥1}和{Yn，n≥1}均为独立同分布的非负随机序列，其分布函数分别为G(x)=Pr{X≤x}和F(y)=Pr{Y≤y}，且G(0)=F(0)=0，{N(t)，t≥0}是一个强度为λ的齐次Poisson过程。

经典风险模型的盈余过程为U(t)=u+ct-S(t)，t≥0，其中:为保险公司的初始盈余;c为单位时间保费率。

在经典风险模型基础上，很多学者引入了再保险，即原保险人将部分风险转移给再保险人，同时需支付给再保险人相应的保费，于是原保险人的盈余过程相应地变为

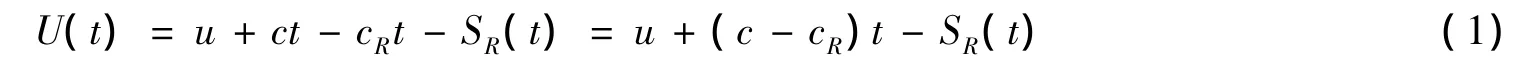
一般情况下采用期望值保费原理，即 c=(1+θ)λE(Y)，cR=(1+ξ)λE［Y-Z(Y)］，θ和ξ分别为原保险和再保险的安全负载(假定ξ≥θ＞0，否则会存在套利的机会)，于是式(1)相应变为

为简化记号，令m=λ{(1+θ)E(Y)-(1+ξ)E［Y-Z(Y)］}，盈余过程 (2)变为 U(t)=u+mt-SR(t)。为了保证保险公司存在一定的利润，需假定:E［Z(Y)］＜mE(X)。

在上述再保险风险模型的基础上，本文考虑利率风险。设常数利息力δ≥0，破产时刻与破产概率分别为，其中 Uδ(t)表示 t时刻的盈余。该模型的盈余过程为

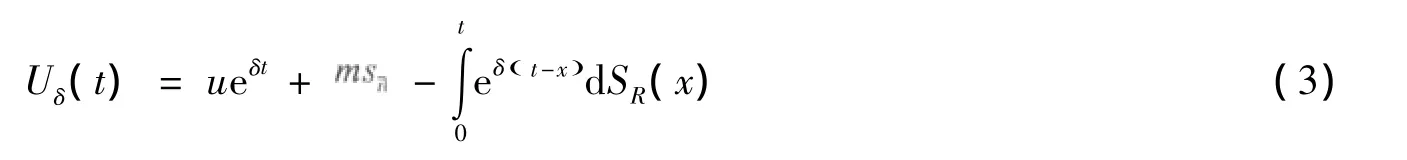
2 主要结果

定理1 存在唯一正常数R，使得成立。

证明令，易知的凸性，可知，存在唯一的正常数R，使得h(R)=1，R称为Lundberg调节系数。

定理2 对于盈余过程 (3)，设R为定理1中的常数，则 ψδ(u)≤e-Ru，即得到破产概率的Lundberg上界。

证明设 ψδ(u;n)为第 n次索赔前破产的概率，则有令 β-1=则，且

下面采用归纳法证明 ψδ(u;n)≤e-Ru。

令X1和Y1分别为第1次索赔的时间间隔和索赔额，有

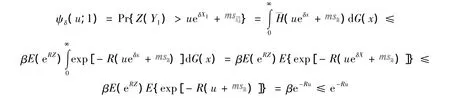
假设 ψδ(u;n)≤e-Ru，下证 ψδ(u;n+1)≤e-Ru。事实上

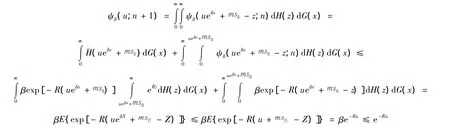
由归纳法可知，任意n≥1，ψδ(u;n)≤e-Ru，于是有

定理3 对于盈余过程(3)，其破产概率满足如下积分方程

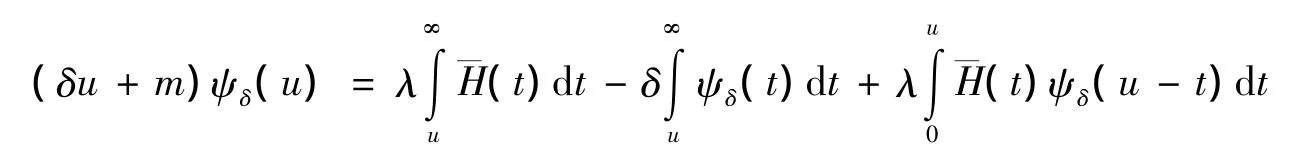
其中H(z)为Z(Y)的分布函数。

证明考虑一个很小时间区间［0，t］，假定在该区间内，最多只可能发生1次索赔，对生存概率进行分解，有

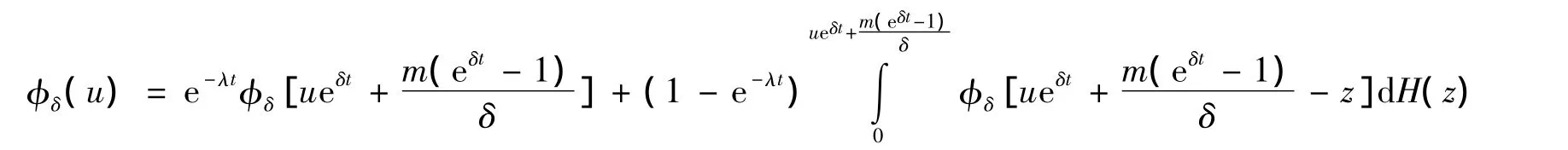
两边关于t求导，有

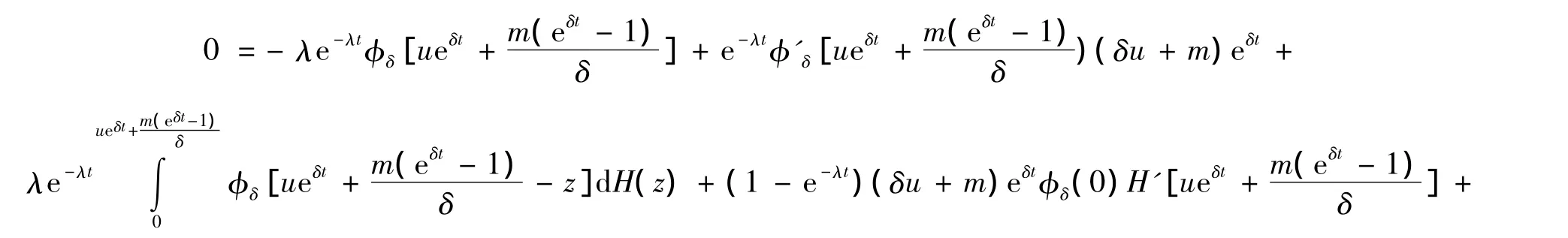
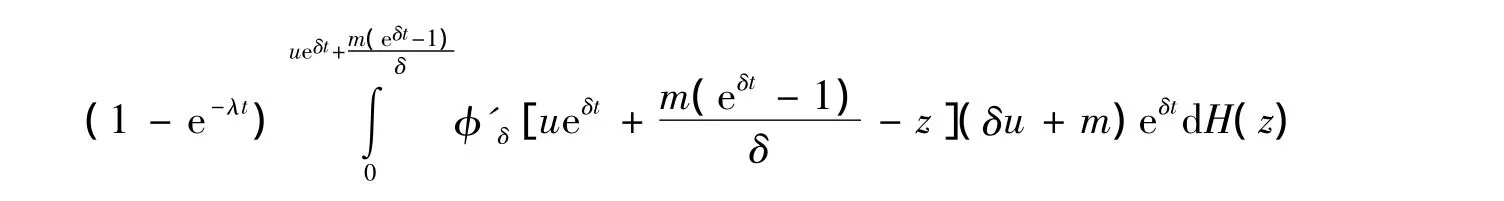
对上式，令t→0，整理得到

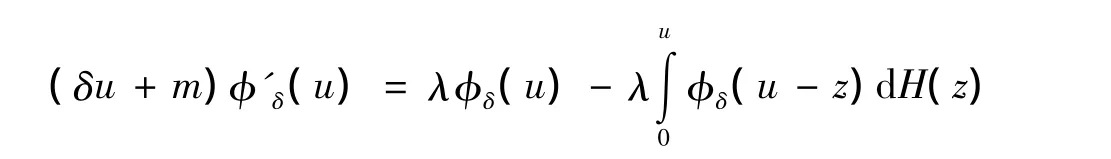
对上式用 t代替 u，并在区间［0，u］积分有

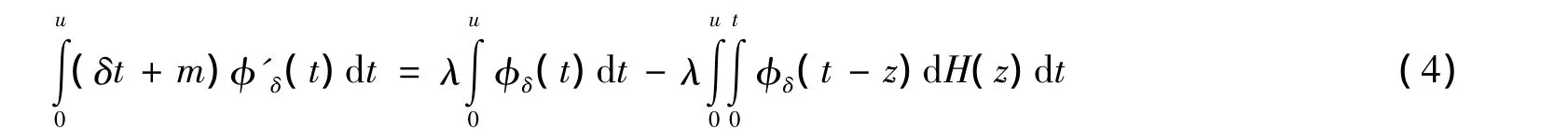
对上式，左右两边分别进行化简，因为

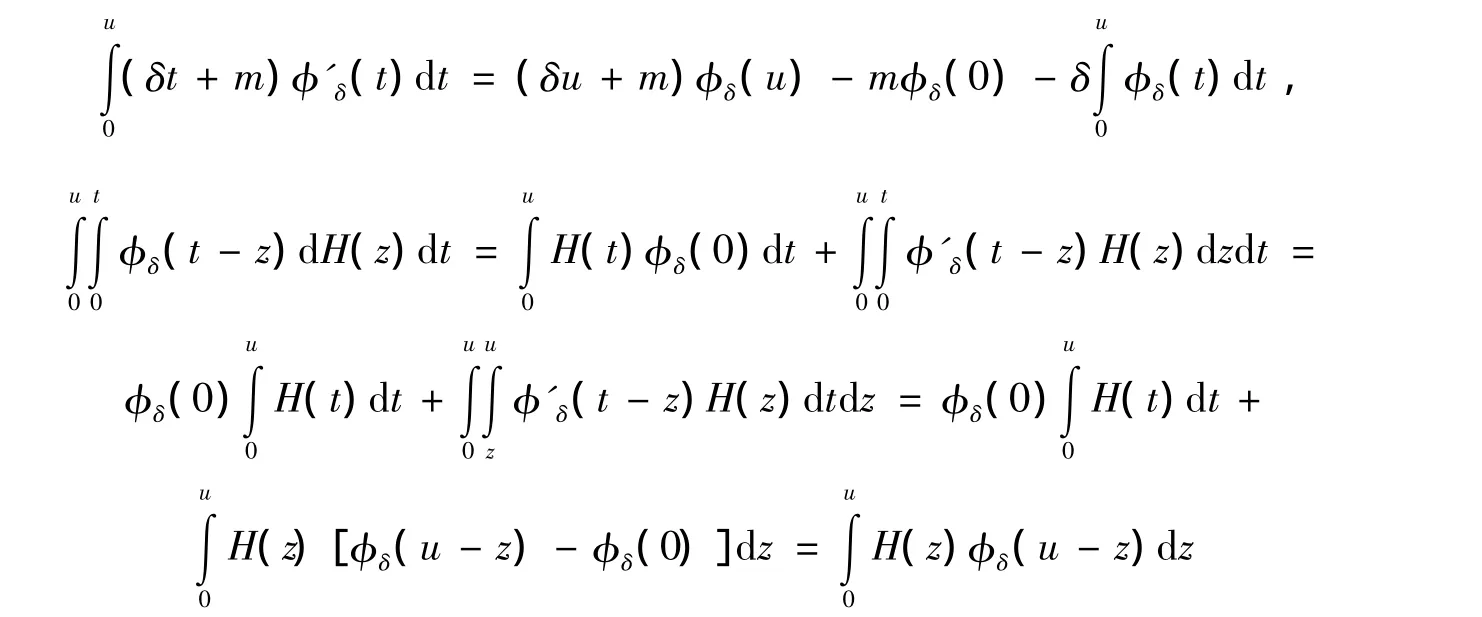
所以，式(4)变为

根据破产概率 ψδ(u)=1-φδ(u)，上式进一步变为

由定理2 可知，ψδ(u)≤e-Ru，故当 u→∞ 时，(δu+m)ψδ(u)→0。

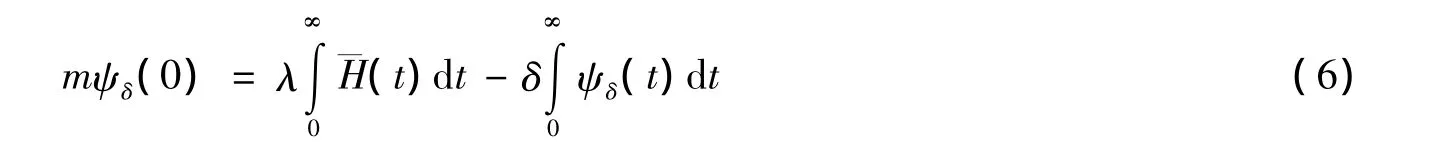
对式(5)两边取极限(u→∞)，有将式(6)代入式(5)，得到破产概率的积分表达式

注:

3 实例

下面给出在经典风险模型中，在索赔额服从指数分布，再保险类型为成数再保险情形下，原保险人破产概率的表达式。

考虑经典风险模型，假定:①被保险人的损失服从参数为β的指数分布，即Y～exp(β);②再保险形式为参数为α的成数(比例)再保险，Z(Y)=αY，0≤α≤1。由假定①和②知，原保险人的损失分布函数为

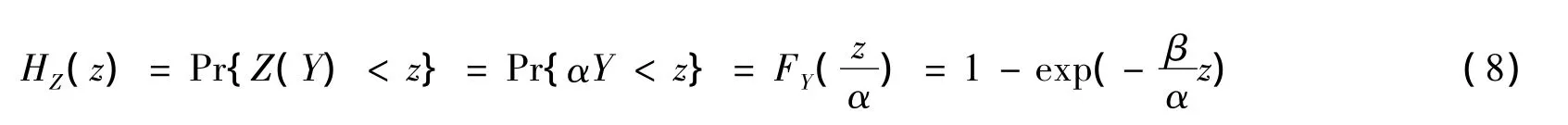
对式(7)进行变形，有

将式(8)代入式(9)，可得

上式两边关于u求导，整理得

对上式关于u求导，得

注:若不考虑利率及再保险，即 δ=0，α=1，m=c=λ(1+θ)E(Y)，则 式(12)变为

由式(6)可知 ψ(0)=1/(1+θ)，且由定理 2有，于是方程 (13)的解为 ψ(u)=，这就是经典风险模型中索赔额服从指数分布的破产概率表达式［8］。

4 结束语

本文围绕经典风险模型盈余过程U(t)=u+ct-S(t)进行研究，将该模型进行推广，引入了再保险和利率的影响，将原来模型中的保费收入以及索赔均进行了相应的改进，使得改进后的模型更加符合实际，且更具一般性。如将本文的模型条件特殊化，即回到了经典风险模型。

［1］Cai J.Discrete time risk models under rates of interest［J］.Probability in the Engineering and Information Sciences，2002，16:309-324.

［2］Cai J，Dickson D.Upper bounds for ultimate ruin probabilities in the Sparre Andersen model with interest［J］.Insurance:Mathematics and Economics，2003，32:61-71.

［3］Cai J，Dickson D.Ruin Probabilities with a Markov chain interest model［J］.Insurance:Mathematics and Economics，2004，35:513-525.

［4］刘东海，刘再明.利率相依的离散时间风险模型的破产问题［J］.经济数学，2008，25(2):126-131.

［5］Dickson D，Waters H.Reinsurance and ruin［J］.Insurance:Mathematics and Economics，1996，19:61-80.

［6］Liang Z，Guo J.Optimal proportional reinsurance and ruin probability［J］.Stochastic Models，2007，23(2):333-350.

［7］Liang Z，Guo J.Upper bound for ruin probabilities under optimal investment and proportional reinsurance［J］.Applied Stochastic Models in Business and Industry，2008，24(2):109-128.

［8］吴岚，王燕.风险理论［M］.北京:中国财政经济出版社，2006.