Mathieu方程与束流冷却对同步运动的影响
2012-07-05罗晓华何为
罗晓华 何为
(1.重庆交通大学 图书馆,重庆 400074;2.重庆大学 电气工程学院,重庆 400044)
其中e是电子电荷,h是谐波数,V是加速电压,E是同步粒子能量,β=v/c是粒子无量纲速度。不失一般性,考虑φs=0的稳态 (stationary state)情形。当φs=0时,方程 (1)退化为
1944年,苏联物理学家维克斯勒 (次年,麦克米兰)发现,在高频电场中运动的带电粒子具有保持相位稳定的能力,并指出适当选择同步相位,即可实现非同步粒子的能量补偿。从此,加速器的能量上限实现了质的突破,质子能量从当初的107eV量级提升到当今的1013eV量级。遗憾的是束流能量和束流强度不能兼得。正是这对矛盾激励着人们不断对加速器技术进行探索,并取得了一个又一个的突破,储存环技术和束流冷却技术便是典型的例子。直到今天,加速器的束流动力学问题依然是人们关注的重要问题之一[1-14]。本文关心的正是束流冷却对同步运动的影响。值得注意的是,随着人们认识能力的不断提高,先后认识了束流动力学的线性、非线性和复杂性,而本文就试图利用Mathieu方程的稳定区和不稳定区 (禁带)来讨论系统的稳定性。为此,在经典力学框架内,把周期冷却的同步运动方程化为Mathieu方程,系统呈现出一系列稳定区和不稳定区;对可能存在的一阶不稳定区进行了讨论,用摄动法导出了它的边界曲线和禁带宽度,并讨论了禁带穿越和同步运动的稳定性,导出了束流冷却一次谐波振幅的临界值。
1 运动方程
束流冷却通常是在环形加速器 (比如同步加速器、储存环等)的一个或几个直线段上安装冷却器来实现的。当粒子通过冷却器时,用一束冷 (发射度小)的电子同它一道运动,并将整个离子束浸泡其中。如果选择电子的速度与离子速度相等,离子和电子在运动方向保持同步,同时它们之间还将通过“热”运动彼交换横向能量,使得比较热的离子束逐渐变冷。换句话说,由于束流冷却,离子的Betatron振荡将逐渐衰减,而同步振荡也将逐渐衰减。
在理想情况下,如果选择相位φ和动量分散系数δ为正则坐标,θ为独立变数,粒子同步运动方程可表示为[7,13-14]

其中e是电子电荷,h是谐波数,V是加速电压,E是同步粒子能量,β=v/c是粒子无量纲速度。不失一般性,考虑φs=0的稳态 (stationary state)情形。当φs=0时,方程 (1)退化为

设系统的冷却系数为μ(θ),对于动量分散为δ的粒子束,经过“长度”为Δθ的冷却后,衰减量Δδ可表示为 Δδ= -μ(θ)δΔθ。于是,正则方程 (2)可化为[7]

或

其中
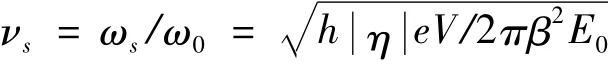

其中ε是小参数,仅表示伴随项是O(ε)级小量。将μ(θ)按Fourier级数展开
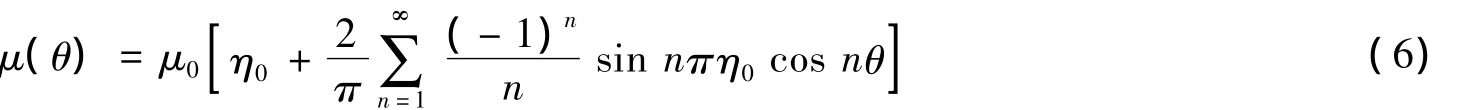
其中Δθ是冷却器“长度”,而η0=Δθ/2π是冷却器的相对长度。令

方程 (5)可进一步化为

其中

式中略去了ε2项。这就是只关心弱冷却情况,而μ(θ)由式 (6)给出。将式 (6)和 (9)带入方程(8),可得粒子同步运动方程

其中

是由于周期冷却产生的n次谐波振幅。方程 (10)是一般的Hill方程,它的系数包含了所有Fourier分量,这个系统将存在和共振与差共振。但是由于这些组合共振都比较弱,感兴趣的是整数共振或半整数共振。由式 (10)可得n次谐波激励的同步运动方程为

2 系统的稳定性
作变数变换

方程 (12)化为

其中参数

方程 (14)是一个标准的Mathieu方程。一次项的系数`是φ的周期函数。根据Flogue定理,方程 (14)的解具有如下性质
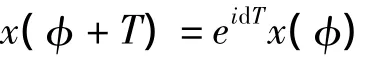
其中d是加速器格子周期,而T是粒子运动周期。粒子在周期中场运动时,它的能量将分裂成带。事实上,系统的稳定性与参数 (q,ε)的分布有关,在参数 (q,ε)平面上,系统出现了一系列稳定和不稳定区。当→0时,如果q>0,系统是稳定的;q<0系统不稳定。不过,随着的增加,即使q<0,系统也可能是稳定的。由于方程 (14)包含振动部分cos 2φ,在q>0的右半平面内出现了一系列稳定区和不稳定区。当→0时,这些不稳定区退化为一点,且全都落在ε=0的横轴上,这些点由方程

给出,并分别称为一阶、二阶、三阶等不稳定区。对于一次谐波 (n=1)激励,由式 (15),(16)可知,这些不稳定区对应于νs=1/2,1,3/2,…,共振。这就是说,由于束流冷却将激发出不同阶次的整数共振或半整数共振。图1给出了数值结果。一般说来,在参数 (q,ε)平面上,这种稳定和不稳定区有无限多个。对于具体情况只有一个或少数几个稳定区和不稳定区起作用。下面对一阶不稳定区(νs=1/2)做进一步分析。
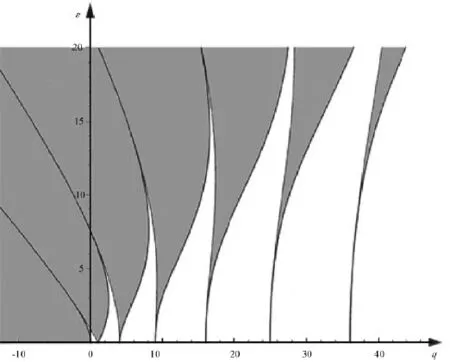
图1 Mathieu方程的稳定与不稳定区 (阴影区域)
3 Mathieu方程的一阶不稳定区及其禁带宽度
利用摄动法[15-16]求解方程 (14)。注意到方程 (14)中的 (是一个小参数,可将x和q按它展开
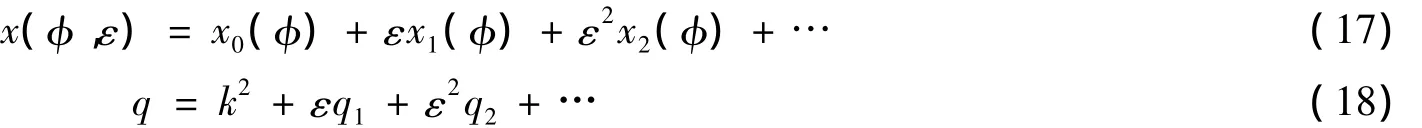
将式 (17)和 (18)代入方程 (14),比较 (的同次幂系数,可得逐次近似方程
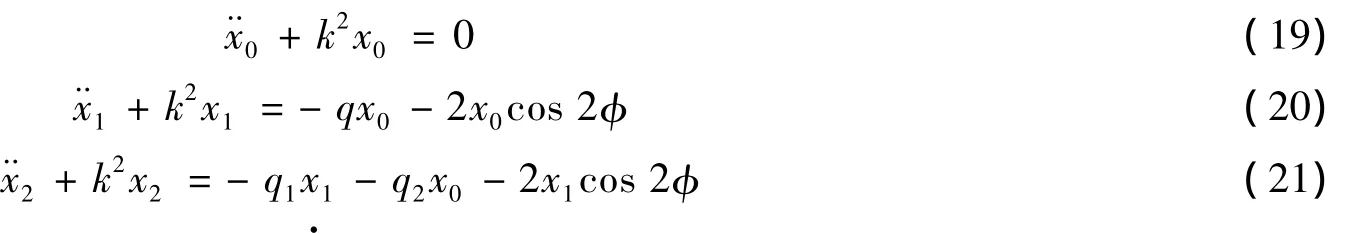
方程 (19)的解可表示为

上式表明,当k为偶数时,x0是周期为π的周期函数,当k为奇数时,x0是周期为2π的周期函数。我们以k=1为例,求禁带的边界方程和相应的解。
将式 (22)代入方程 (20),并令k=1,可得
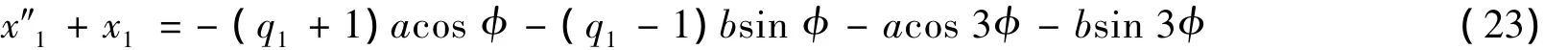
消去方程中的久期项,要求

于是方程 (23)化为

联立求解方程 (24)和 (25),可得

和
航空发动机装配过程数据能够映射为任务、物料、工艺、质量4个视图上的对应信息,分别回答了“由谁在何时来执行哪个任务”、“对哪些物料进行装配”、“如何装配”和“记录哪些质量信息”的问题,4个视图之间存在的逻辑关联关系如图2所示。

于是,方程 (26)的解可表示为

或

将式 (27)、(29)代入方程 (21),可得二级近似方程
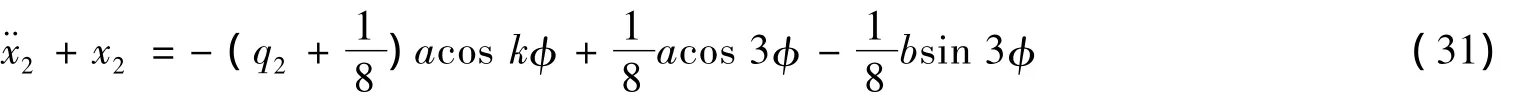
消去久期项,可得

精确到二次近似,一阶不稳定区的一条边界曲线和这条边界曲线上的解可表示为

同样,将式 (28)、(30)代入方程 (21),并用类似的方法,可求得一阶不稳定区的另一条边界曲线和这条边界曲线上的解为

由式 (33)和 (35),可求得一阶不稳定区的禁带宽度

4 系统的临界性质
注意到当谐波数n=1时,由式 (15)可知,同步运动的Betatron频率可表示为=q/4。微分该式,由式 (37)可将一阶不稳定区的禁带宽度表示为

再注意到粒子穿越禁带时振幅呈指数增长,设φ0(因而x0)是粒子进入禁带时的“初始”振幅,穿越禁带后的振幅φ(因而x)可表示为

其中θ是粒子在禁带中转过的角度 (或“停留”的时间)。当φ满足条件
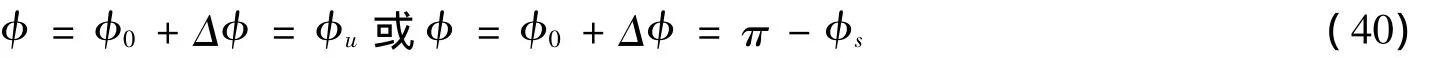
时,系统处于临界状态,其中φu和π-φs是同步运动的两个不稳定点,φs是系统的同步相位 (在本文中φs=0)。换句话说,当离子穿越禁带,相位呈指数增长,如果相位的振幅φ<φu和φ<π-φs,系统是稳定的,否则系统不稳定。由式 (15)、(16)和 (38)可得束流冷却的一次谐波振幅临界值

或

其中ωs是同步粒子振荡频率,Tc是同步粒子穿越禁带的临界时间。当δ1<δ1c系统是稳定的,否则系统不稳定。
5 结语
由于冷却效应,同步运动方程化为了参数激励的Matheiu方程,由于参数激励,系统出现了一系列稳定和不稳定区。这就是说,由于束流冷却,系统的同步运动将在νs=1/2,1,3/2,…,处出现共振。本文从系统的正则方程出发,在经典力学框架内和弱冷却近似下,把粒子的同步运动方程化为Mathieu方程,利用摄动法导出了一阶不稳定区 (νs=1/2)的边界曲线和禁带宽度。指出了由于冷却效应,当粒子穿越禁带后的相位φ=φ0+Δφ等于不稳定相位时,粒子处于临界状态,并由此导出了束流冷却的一次谐波激励振幅的临界值或。当 δ1< δ1c时,系统是稳定的,否则系统不稳定。
[1]Dumas H S,Ellison J A,Vogt M.First-Order Averaging Principles for Maps with Applications to Accelerator Beam Dynamics[J].SIAM J Appl Dyn Syst,2004,3(4):409 -432.
[2]罗诗裕,邵明珠,胡西多.二维晶化束的平均场概念与单粒子模型(I)[J].高能物理与核物理,2004,28(1):96-99.
[3]胡西多,罗诗裕,邵明珠,等.二维晶化束的平均场概念与单粒子模型(II)[J].高能物理与核物理,2004,28(2):196-199.
[4]Derbenev Y.Six - dimensional muon beam cooling using a homogeneous absorber:Concepts,beam dynamics,cooling decrements,and equilibrium emittances in a helical dipole channel[J].Phys Rev ST Accel Beams,2008,5:041002.(20 pages)
[5]Qiang J,Lidia S,Ryne R D,et al.Three-dimensional quasistatic model for high brightness beam dynamics simulation[J].Phys Rev ST Accel Beams,2006,9:044204.(10 pages)
[6]Helmut Wiedemann.Particle accelerator physics[M].Berlin:Springer,2007:215 -221.
[7]Lee S Y.Accelerator Physics[M].2nd ed.Shanghai:Fudan University Press,2006:288 -295.
[8]Schroeder C B,Shadwick B A,Esarey E.Radiative damping and electron beam dynamics in plasma- based accelerators[J].Phys Rev E,2006,74:026501.(14 pages)
[9]Ferrario M,Alesini D,Bacci A,et al.Measurement of the Double Emittance Minimum in the Beam Dynamics of the Sparc High-Brightness Photoinjector[J].Phys Rev Lett,2007,99:234801.(5 pages)
[10]Stokes R H,Crandall K R,Stovall J E.Rf quadrupole beam dynamics[J].IEEE Transactions on Nuclear Science,2007,26(3):3469-3471.
[11]Zhang Z L,Jameson R A,Zhao H W,et al.Beam dynamics design of an RFQ for a planned accelerator,which uses a direct plasma injection scheme[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment,2008,592(3):197 -200.
[12]Piel C,Dunkel K,Kremer F,Pekeler M.Phase 1 Commissioning Status of the 40 MeV Proton/Deuteron Accelerator SARAF[C]//Proceeding of EPAC08.Genoa:2008.
[13]范丽仙,罗诗裕,邵明珠.正弦平方势与环形加速器的弯晶束流引出[J].原子核物理评论,2011,28(1):63-67.
[14]肖慧娟,罗诗裕,邵明珠.多尺度法与准等时同步加速器粒子纵向运动的稳定性[J].原子核物理评论,2011,28(3):300-304.
[15]Nayfeh A H.Introduction to Peturbation Techniques[M].New Youks:John Wiley& Sons,1981:226-240.
[16]罗诗裕,邵明珠,罗晓华.正弦平方势与应变超晶格位错动力学[J].中国科学:物理学,力学和天文学,2010,40(2):207-212.
