《易经》学说的现代群论解释
2012-07-05熊辉蔡思洁
熊辉 蔡思洁
(东莞理工学院 计算机学院,广东东莞 523808)
1 八卦与九宫的代数性质
九宫图是阶数最低的纵横图,又名三阶幻方。据曲安京考证[1],最早提到九宫图形制的文字大约见于西汉时期的纬书,如《易乾凿度》称:
太乙取其数以行九宫,四正四维皆合于十五。
文王后天八卦图中的卦象排列有这样的歌词来帮助记忆:
一数坎兮二数坤,三震四巽数中分。
五寄中宫六乾是,七兑八艮九离门。
大德南怀瑾感叹曰:由此歌谣,古人教育方法之高明可见一斑。
后天八卦所对应的排列方式其实就是九宫阵,用现代的矩阵表示就是

在该矩阵中,除了相对的两个卦加起来合而为十和任何一行,一列、主对角线、副对角线上的三数之和都是十五之外,它还满足很多代数恒等式。把每行的三个数字分别合为一个三位数,如第一行、第二行、第三行分别为618、753、294;再把从左到右每行的三个数字从右到左分别合为一个三位数,如第一行、第二行、第三行分别为816、357、492。简单的计算就能验证到,他们不但和相等,而且平方和也相等,列表如下:
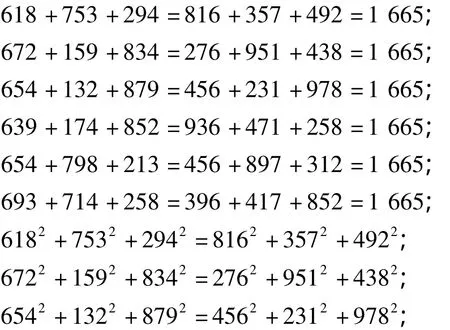
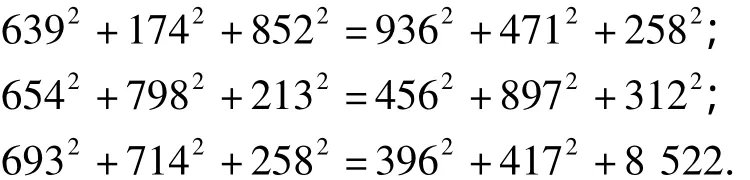
此外,该方阵还有更令人叹为观止的性质,就是矩阵在乘方后,会保持某种不变性。有关这一运算性质的详细叙述请参阅文献 [2]。本文的主要目的,是希望把这些不变性纳入“近世代数”的范畴,并建立相应的代数群,利用代数群论的知识,来给八卦九宫中的这些算法一个现代数学和科学上的合理解释。
2 消息运算群
1~9这九个数字组成的三阶方阵总共有9!=362 880种,但只有其中的八种满足以上的代数恒等式(这些恒等式本文中合称之为九宫性质)。为什么刚好是八种而不是其他数目,这可能是个很耐人寻味的问题。因为八不但是八卦的总卦数,也是具有代表性的方位的总数,更是90度旋转变换和镜面反射的种类之和。
在建立群论之前,首先简单介绍一下代数群的数学概念[3]。
定义1 设A是一个非空集合,如果对任意两个元素α1,α1∈A,都满足α1◦α1=α∈A,则称“◦”是一个定义在A上的代数运算。如果对任意α∈A,都满足σ(α)∈A,则称“σ”是一个定义在A上的代数变换。
例1 由于任意两个整数相加或相乘还是整数,所以普通的加法和乘法是定义在整数集合上的一个代数运算。
例2 设σ1(α)=2·α,其中·为普通乘法。因为偶数乘以2仍旧是偶数,因此σ1是偶数集合上的代数变换。
定义2 设A是一个非空集合,如果在A上满足以下三点:
1)A上的代数运算对任意元素a,b,c∈A满足结合律:
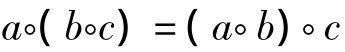
2)A中有唯一的元素e,称为单位元,且对任意元素a∈A满足

3)A对任意元素a∈A,A中都有唯一的元素a-1,称为a的逆元,且满足
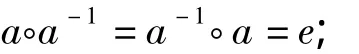
则称A对于运算◦成为一个群。如果对任意元素a,b∈A还满足
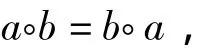
则称A是一个交换群或Abel群。
在阴爻和阳爻中每次任取一爻,连取三次就可以得到八卦。设集合
B={乾,兑,离,震,巽,坎,艮,坤}。
令阳爻为1,阴爻为0,从初位到上位依次把八卦转换成二进制,则消息运算可重新定义如下。定义3 设B是如上的八卦二进制集合
B={111,110,101,100,011,010,001,000},
任取其中的两个元素,定义一种消息运算◦,表示对应位的数字相加,然后重新组成一个三位二进制数,即得到一个新卦。需要注意的是,在二进制中,1+1=10,取个位的话则为1+1=0,然后向前进一位,如果进位后变成四位数的话,则取后三位。
例3 取离卦 (101)和艮卦 (001),根据消息运算,有
101◦001=(1+0)(0+0)(1+1)=100(即艮卦)。
取兑卦 (110)和离卦 (101),根据消息运算,有
110◦101=(1+1)(1+0)(0+1)=1 011=011(即巽卦)。
定理1 设B是如上的八卦二进制集合,则对于消息运算◦,B是一个Abel群。
证明 对于任意两个元素,由于普通加法满足交换率,因此只要B是一个群的话,则必然也是一个交换群,即Abel群。因此,只要证明B是一个群就可以了。因普通加法满足结合律,因此消息运算◦也满足结合律。
由于坤卦α1=000在加法中不起作用,即与其它卦α1,…,α8做消息运算后满足
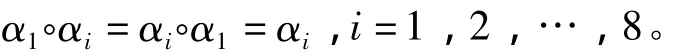
因此坤卦是B的单位元。另外,由于1+0=1,0+1=1,0+0=0,1+1=0。
因此对应于单位元坤卦来说,每个卦在集合居中都有唯一的逆元。如乾卦的逆元为艮卦,兑卦的逆元为坎卦,离卦的逆元为巽卦,震卦的逆元为震卦自身,坤卦的逆元也是坤卦自身。
八卦群的这一性质可以用另外一个也恰好有八个元素的Abel群来印证。设

在集合S中定义一种代数运算◦,记为⊗,得出的乘积是正常乘法之积的后五位数,如:

简单的验证就可以发现,交换率和结合率对这种变态乘法仍然成立,即

这个集合S满足“封闭性”,即任意两个元素经过⊗运算后,得到的“积”仍旧属于S;且由于
90 625⊗90 625=90 625,
因此称90 625单位元。另外,集合S可以完全由其中任一元素通过⊗运算单独“生”出来,如取21 875,先定义an为a×a×… ×a(共n个相乘)乘积的最后五位数,则有

由于八次方后得到单位元,因此再乘方的话就会产生循环。也就是说,这个集合或代数群只有八个元素。群S和八卦群B有很多相似之处,因此从具体的角度而言,可以用群S来研究八卦群的性质。群S可以由其中任何一个元素全部衍生出来,最后归于单位元90 625;而八卦群B也可以从其中任一个元素生出来,并且也最后归于单位元坤卦。从乾卦开始,对应二进制数每次递减1,直到等于0,这就是坤卦。这一过程其实就相当于上述群S中的乘方运算。这一对应实例似乎可以说明,八卦体系如果采用近世代数中的群论来研究的话,应该可以找到新的生机和新的科学与哲学意义。
3 代数变换群
前文说过,满足九宫性质的三阶方阵只有八种,这暗合着八卦的种类,但这也许只是个巧合。在这一小节里,要建立一个正交变换群,这个群里也刚好只有八个元素,并可以一一对应到八种三阶幻方。显然,八种三阶幻方都是都过(1)式的矩阵A多次逆时针转置或行行交换与列列交换而产生的,下面,我们将从群论的角度来说明这一过程。
以正方形的中心点为坐标原点,建立直角坐标系,如图1所示。根据这个图和坐标系,定义一种代数变换 (见定义1),称为正交变换。
定义4 设A是一个非空集合,σ是一个定义在A上的代数变换,如果该变换还保证原图中任意两点之间的距离在经过σ变换后能保持不变,则该变换称为正交变换。
由正交变换的性质,不难看出,正方形关于坐标原点恰好有八种正交变换。设变换σ1表示逆时针旋转90度,变幻σ2表示关于镜面反射。则这八种正交变换可以组成一个八元素的集合,即

图1 从正方形的中心点为坐标原点,建立直角坐标系

如果对上图中的直角坐标系定义上北下南、左西右东,则恒等变换就相当于乾卦在西北方的八卦图。而变换σ21,即旋转180度,这时的卦图方位就是中国古代经典的上南下北、左东右西。
三阶方阵中满足九宫性质的矩阵只有八种,其根本的数学原理,是由自然数的性质决定了,但其体现形式是多种多样的。在众多的体现形式中,最具有现代数学和科学意义的,就是用近世代数的群论的方法,构造代数运算群和代数变换群。
[1]曲安京.中国古代科学技术史纲:数学卷[M].沈阳:辽宁教育出版社,2000:378.
[2]熊辉.代数与中国古代经典[M].北京:中国出版集团,2010.
[3]北京大学数学系.高等代数[M].2版.北京:高等教育出版社,1999.
