强拟闭集与强拟连续

吴耀强

(宿迁学院教师教育系,江苏 宿迁 223800)

强拟闭集与强拟连续

吴耀强

(宿迁学院教师教育系,江苏 宿迁 223800)

利用半闭集引入强拟闭集概念,研究了半开集、强拟开集、强拟闭集概念之间的关系,得到了强拟闭集是连续闭映射下的不变量及其相关性质;最后给出强拟连续概念并得到其等价刻画.

拓扑空间;半开集;强拟闭集;强拟连续

1 引言

自一般拓扑学产生以来,许多拓扑学者在开集这一概念的基础上,引入了一些近似开集的概念,如Levine、Stone、Mashhour等先后分别引入半开集、正则开集、准开集等概念,研究半开集等近似开集理论已成为一般拓扑学中重要的专题,并且得到了一些好的结果.那么,我们能否采用半开集概念加以定义其它近似开集？回答是肯定的,同时这无疑是全新的研究方式.本文基于半开集定义了一种新的近似开集—强拟闭集,并由强拟闭集概念进一步引入了强拟开集、强拟连续等概念,得到许多有趣的结果.文中引入的这些概念的名称可能在其他文献中出现过,但它们的内涵却不尽相同.

2 强拟闭集

本文中X是非空集合,(X,T)是拓扑空间,用T与F分别表示X的开集族与闭集族,若A⊂X,用A°和A-分别表示为A的内部和闭包,本文未申明的概念与记号均引自文献[1-3].

定义2.1设(X,T)是拓扑空间,A,B⊂X,

(1)[1]如果存在开集U,使得U⊂A⊂U-,则称A为半开集,以SO(X)表示半开集族;

(2)[2]若X-B∈SO(X),则称B为半闭集,以SC(X)表示半闭集族.

注2.1文献[2]给出半闭集的等价定义:设(X,T)是拓扑空间,B⊂X,

(1)X-B∈SC(X)⇔存在闭集F,使得F°⊂B⊂F;

(2)X-B∈SC(X)⇔B⊃B-°.

定义2.2设(X,T)是拓扑空间,C⊂X,如果存在半闭集B,使得B°-⊂C⊂B,则称C为强拟闭集,以SPC(X)表示强拟闭集族.

定理2.1设(X,T)是拓扑空间,C⊂X,C∈SPC(X)⇔C⊃C-°-.

证明若C⊃C-°-,由定义2.2易得C∈SPC(X);反之,设C∈SPC(X),则存在半闭集B,使得B°-⊂C⊂B,又B∈SC(X),由注2.1知B⊃B-°,这样B-°-=(B-°)°-⊂B°-,有C⊃B-°-,又由于B⊃C,易得B°-⊃C°-,故C⊃C-°-.

引理2.1[3]设(X,T)是拓扑空间,E⊂X,则E°′=E′-,E′°=E-′,E′表示E的余集.

注2.2(1)由引理2.1我们可以把强拟闭集的余集定义为强拟开集,则由B°-⊂C⊂B,可得B′⊂C′⊂(B°)-′=(B′)-°,即D为强拟开集当且仅当存在半开集A使得A⊂D⊂A-°,并以SPO(X)表示强拟开集族;

(2)显然T⊂SPO(X)⊂SO(X);F⊂SPC(X)⊂SC(X);

(3)设(X,T)是拓扑空间,D⊂X,D∈SPO(X)⇔D⊂D°-°.

定理2.2设(X,T)是拓扑空间,{Cγ}γ∈Γ是X的一个强拟闭集族(其中指标集Γ非空),则∩γ∈ΓCγ为强拟闭;对偶地,若{Dγ}γ∈Γ是X的一个强拟开集族,则∪γ∈ΓDγ为强拟开.

证明由于任意γ∈Γ,Cγ∈SPC(X),则存在Bγ∈SC(X),使得B°-γ⊂Cγ⊂Bγ,进而∩γ∈ΓB°-γ⊂∩γ∈ΓCγ⊂∩γ∈ΓBγ,又∩γ∈ΓB°-γ⊃(∩γ∈ΓB°γ)-,且∩γ∈ΓB°γ⊃(∩γ∈ΓBγ)°,故

易知∩γ∈ΓBγ∈SC(X),从而∩γ∈ΓCγ∈SPC(X).

命题2.1设(X,T)是拓扑空间,C∈SPC(X),且C°-⊂E⊂C,则E∈SPC(X).

证明由于C∈SPC(X),根据注2.2知C⊂SC(X),使得C°-⊂E⊂C,有E∈SPC(X).

定理2.3设B={Bα}是拓扑空间(X,T)的一个子集族,满足i)F⊂B;ii)若B∈B,且B°-⊂C⊂B,则C∈B.那么SPC(X)⊂B;且SPC(X)是满足i)与ii)最小集族.

证明设E∈SPC(X),则存在半闭集F,使得F°-⊂E⊂F;又F∈SC(X),则存在闭集U,使得U°⊂F⊂U,可得U°-⊂F°-,故U°-⊂F°-⊂E⊂F⊂U,由i)得U∈B;再由ii)可得E∈B,所以SPC(X)⊂B.

假设A={Aα}为任意一个满足i)与ii)的拓扑空间X的一个子集族,则有F⊂A,所以A包含了所有闭集;另外,设A∈SPC(X),则存在半闭集F,使得F°-⊂A⊂F;所以A∈A,即A包含了所有的强拟闭集.

定理2.4设Y是(X,T)的一个子空间,且C⊂Y⊂X,若C∈SPC(X),则C∈SPC(Y).

证明设C∈SPC(X),则存在半闭集B,使得B°-⊂C⊂B;且C⊂Y⊂X,这样可得B°-∩Y⊂C∩Y=C⊂B∩Y;下证B∩Y为子空间Y中的半闭集.事实上,由于B是半闭集,则存在闭集F,使得F°-⊂B⊂F;进而F°∩Y⊂B∩Y⊂F∩Y;根据F°=F°(Y)∩Y°,(这里F°(Y)表示F在子空间Y中的内部,下同)即得(F∩Y)°(Y)⊂F°∩Y,所以(F∩Y)°(Y)⊂B∩Y⊂F∩Y,令U=F∩Y,显然U为Y中的闭集,且U°(Y)⊂B∩Y⊂U,故B∩Y为子空间Y中的半闭集.

此外,由于B°-∩Y=(B°)-(Y),且B°=B)°(Y)∩Y°,则

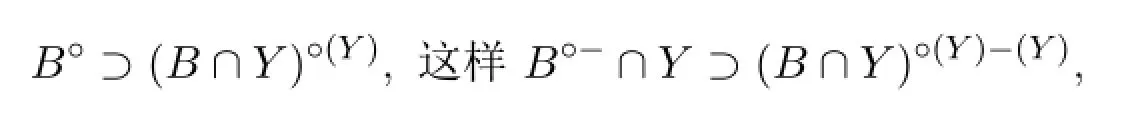
进而(B∩Y)°(Y)-(Y)⊂C⊂B∩Y,由前知B∩Y为子空间Y中的半闭集,所以C∈SPC(Y).

注2.3定理2.4之逆不真.例如:令

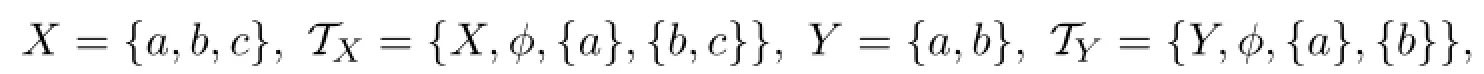
取C={b},显然C°⊂Y⊂X,且C为Y中闭集,也为Y中强拟闭集,但C-°-={b,c}/⊂C,根据定理2.1可知C/∈SPC(Y).

命题2.2设(X,T)是拓扑空间,则有下列结论:(1)若F是闭集,则F-F°为X中无处稠密子集,即其闭包不含内点;(2)[2]若U是开集,则U-U为X中无处稠密子集;(3)若F是X中的无处稠密子集,则F′为X中的稠密子集.

证明(1)由于F-F°=F∩(F°)′,易知F与(F°)′均为X中的闭集,进而F-F°为X中的闭集,故(F-F°)-°=(F-F°)°=∅;

(2)证明见文献[2];

(3)由设知F-′-=X,则F-′为稠密子集,又F-′=F′°⊂F′,即F-′-⊂F′-,故F′-=X.

定理2.5设C是拓扑空间(X,T)的强拟闭集,则有下列结论:(1)存在集合F与U,使得C=F°-∪U,其中F与U满足:①F∈F;②U为无处稠密子集;③C=F°-∩U=∅. (2)存在集合F与T,使得C=F∩T,其中F与T满足:①F∈F;②T为稠密子集;③F∪T=X.(3)存在集合F与S,使得C=F-S,其中F与S满足:①F∈F;②S为无处稠密子集;③S⊂F.

证明由设知C∈SPC(X),则存在半闭集B,使得B°-⊂C⊂B;又B∈SC(X),则存在闭集F,使得F°⊂B⊂F,从而有F°-⊂B°-⊂C⊂B⊂F.(1)由于C=F°-∪(C-F°-),记U=C-F°-,则F°-∩U=∅.下证U为X中无处稠密子集.事实上U⊂F-F°-⊂F-F°,由命题2.2(1)知F-F°为X中无处稠密子集,故U为X中无处稠密子集.

(2)由于C=F∩(C∪F′),记T=C∪F′,则F′⊂C′⊂F°-′⊂F°′⊂F′-.另外由于C′=F′∪(C′-F′),记V=C′-F′,可得V⊂F′--F′.由命题2.2(2)知F′--F′为X中无处稠密子集,故V为X中无处稠密子集.又由于V′=(C′-F′)′=C∪F′=T,于是根据命题2.2(3)即知T为X中稠密子集,且F∪T=F∪(C-F′)=F∪F′∪C=X.

(3)由于C=F-(F-C),记S=F-C,则S⊂F,且S⊂F-F°-⊂F-F°,由引理2.2(1)知F-F°为X中无处稠密子集,故S为X中无处稠密子集.

注2.4上述结论的逆不真.仅以结论(3)为例说明.

例设X是实数空间,C={x|0≤x≤2}-{1}.令F={x|0≤x≤2},S={1}为X中无处稠密子集,且S⊂F,即满足定理2.5(3)的条件①、②、③,但是

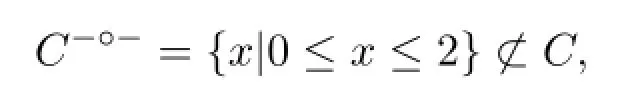
根据定理2.1可知C/∈SPC(X).

定理2.6设(X1,T1),(X2,T2)是两个拓扑空间,X1×X2为它们的拓扑积空间,若A1和A2分别为X1和X2上的强拟闭(开)集,则A1×A2是X1×X2上的强拟闭(开)集.

证明仅证强拟闭集情形.设Ai(i=1,2)分别为Xi(i=1,2)的强拟闭集,则存在Bi∈SC(Xi)(i=1,2),使得B°-i⊂Ai⊂Bi(i=1,2),则又Bi∈SC(Xi)(i=1,2),则存在Fi∈Fi(i=1,2),使得F°i⊂Bi⊂Fi(i=1,2),有

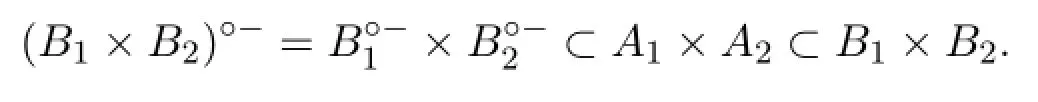
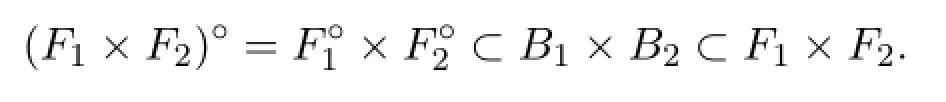
进而B1×B2为X1×X2上的半闭集,故A1×A2是X1×X2上的强拟闭集.

定理2.7设(X,TX),(Y,TY)拓是两个拓扑空间,f:X→Y是连续闭映射,A⊂X,则有下列结论成立:(1)半闭集是连续闭映射下的不变量,即A是(X,TX)中半闭集,则f(A)是(Y,TY)中半闭集;(2)强拟闭集是连续闭映射下的不变量,即A是(X,TX)中强拟闭集,则f(A)是(Y,TY)中强拟闭集.

证明(1)由于A∈SC(X),则∃F∈F,使得F°⊂A⊂F,故f(F°)⊂f(A)⊂f(F),由f连续,易得(f(F))°⊂f(A)⊂f(F),又f为闭映射,则f(F)∈FY,故f(A)∈SC(Y).

(2)由于A∈SPC(X),则∃G∈SC(X),使得G°-⊂A⊂G,故f(G°-)⊂f(A)⊂f(G),由于f(G°)⊂f(G°-),有((f(G))°)-⊂(f(G°-))-,题设f为闭映射,则f(G°-)为闭集,即(f(G°-))-=f(G°-),这样(f(G°))-⊂f(A)⊂f(G),又f连续,则(f(G))°⊂f(G°),,于是(f(G))°-⊂f(A)⊂f(G),由定理2.6(1)可知f(G)∈SC(Y),故f(A)∈SPC(Y).

注2.5定理1.7中条件”闭映射”不可省去,否则上述结论不成立.例如:设X是实数空间,令Y={a,b,c},TY={Y,φ,{a},{b,c}},定义映射f:X→Y,这里∀x∈X,f(x)=b.这样f([0,1])={b},易验证{b}/∈SC(Y),{b}/∈SPC(Y),显然[0,1]是X中闭集,当然也是X中半闭集和强拟闭集.

3 强拟连续

定义3.1[3]设(X,TX),(Y,TY)拓是两个拓扑空间,映射f:X→Y,如果对于Y中任何一个开集U的原像f-1(U)是X中的一个开集,则称f是从X到Y一个连续映射.

定义3.2设(X,TX),(Y,TY)拓是两个拓扑空间,映射f:X→Y,如果对于Y中任何一个闭集F的原像f-1(F)是X中的一个强拟闭集,则称f是从X到Y一个强拟连续映射.

注3.5显然f是从X到Y一个连续映射,则f也是一个强拟连续映射.反之未必一定成立.例如:设X=Y=[0,2],定义映射f(x)=2(0≤x≤1),f(x)=0(1≤x≤2),易验证f在[0,2]上为强拟连续映射,显然f在[0,2]上不为连续映射.

定理3.1设(X,TX)与(Y,TY)是两个拓扑空间,映射f:X→Y,f是强拟连续映射⇔对于Y中任何一个强拟开集O,f-1(O)是X中强拟开集.

证明设O是Y中任意一个开集,令F=O′,则F是Y中一个闭集,由于f是强拟连续映射,由定义3.2知,f-1(F)是X中的一个强拟闭集,根据引理2.1注2(1)知(f-1(F))′是X中的一个强拟开集;又f-1(O)=f-1(F′)=(f-1(F))′,故f-1(O)是X中强拟开集.

反之,设F是Y中任意一个闭集,令O=F′,则O是Y中一个开集,由设可得f-1(O)是X中强拟开集,根据引理2.1注2(1)知(f-1(O))′是X中的一个强拟闭集;又

从而f-1(F)是X中强拟闭集,故f是强拟连续映射.

定理3.2设(X,TX)与(Y,TY)是两个拓扑空间,映射f:X→Y,f是强拟连续映射⇔对于Y中任何一个开集V,f(p)∈V,存在X中强拟开集B,使得p∈B,f(B)⊂V.

证明设V是Y中任意一个开集,由于f是强拟连续映射,根据定理3.1知f-1(V)是X中强拟开集.任取令f(p)∈V,则p∈(f-1V),令B=f-1(V),则

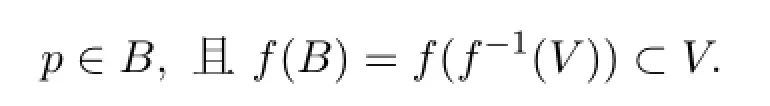
反之,设V是Y中任意一个开集,p∈(f-1V),则f(p)∈V,故存在一个强拟开集Bp,使得p∈Bp,f(Bp)⊂V,这样Bp⊂f-1(f(Bp))⊂f-1(V),故f-1(V)=∪p∈f-1(V)Bp,由定理2.2可知f-1(V)为X的一个强拟开集,根据定理3.1知f为是一个强拟连续映射.

定理3.3设(Xi,TXi)与(Yi,TYi)(i=1,2)是两个拓扑空间,映射fi:Xi→Yi(i=1,2)是强拟连续映射,令f:X1×X2→Y1×Y2,这里f(x1,x2)=(f(x1),f(x2)),则f是强拟连续映射.

根据定理2.6知f-1(V1×V2)为X1×X2的强拟开集.设V是Y1×Y2任意一个开集,由上易知f-1(V)=f-1(∪Bp)=∪f-1(Bp),这里Bp是形如V1×V2的强拟开集,由定理2.2可知f-1(V)为X的一个强拟开集,根据定理3.1知f是一个强拟连续映射.

[1] Levine N. Semi-open sets and semi-continuity in topological spaces[J]. Amer. Math. Monthly, 1963,70(1):36-41.

[2] Crossley S G, Hildebrand S K. Semi-closure[J]. Texas J. Sci., 1971,22(2/3):99-112.

[3]熊金诚.点集拓扑讲义[M].3版.北京:高等教育出版社,2003.

[4]吴耀强.基于半开集的强拟开集运算与性质[J].吉林师范大学学报:自然科学版,2010,31(2):59-62.

Strongly quasi -closed sets and strongly quasi-continuous

Wu Yaoqiang

(Department of Teachers Education, Suqian College, Suqian 223800, China)

First,the concept of strongly quasi-closed sets was introduced by sem i-closed sets,the connections among sem i-open sets,strongly quasi-open sets and strong quasi-closed sets were discussed.Furthermore,the conclusion which strongly quasi-closed setswere invariant under the continuous closed mapping was obtained, some resu lts of strongly quasi-closed setswere given through further research.Finally,the concep t of strongly quasi-continuousm app ing was introduced,then its characterizing theorem was proved.

topological space, semi-open sets, strongly quasi-closed sets, strongly quasi-continuous mapping

O189.11

A

1008-5513(2012)02-0181-05

2010-11-10.

吴耀强(1973-),硕士,副教授,研究方向:拓扑学.

2010 MSC:54A 05