利用改进的(G′/G)-展开法求广义的(2+1)维Boussinesq方程的精确解

赵云梅,杨云杰,将艳

(1.红河学院数学学院,云南 蒙自 661100;2.昆明学院数学系,云南 昆明 650031; 3.思茅师范高等专科学校数学系,云南 普洱 665000)

利用改进的(G′/G)-展开法求广义的(2+1)维Boussinesq方程的精确解

赵云梅1,杨云杰2,将艳3

(1.红河学院数学学院,云南 蒙自 661100;2.昆明学院数学系,云南 昆明 650031; 3.思茅师范高等专科学校数学系,云南 普洱 665000)

利用改进的(G′/G)-展开法,求广义的(2+1)维Boussinesq方程的精确解,得到了该方程含有较多任意参数的用双曲函数、三角函数和有理函数表示的精确解,当双曲函数表示的行波解中参数取特殊值时,便得到广义的(2+1)维Boussinesq方程的孤立波解.

广义的(2+1)维Boussinesq方程;齐次平衡;改进的(G′/G)-展开法;精确解

1 引言

本文研究下列广义的(2+1)维Boussinesq方程[1]:

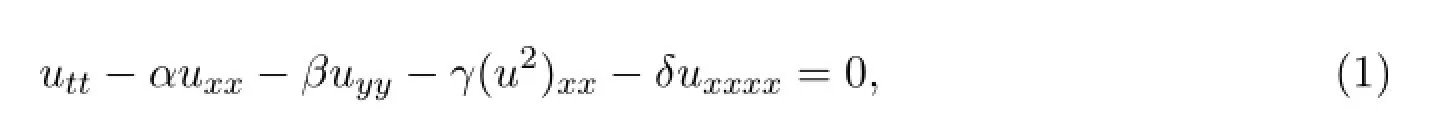
其中α,β,γ和δ是任意常数,γδ/=0.

由于Boussinesq方程在物理学中有很好的应用,故被许多学者用不同的方法研究,如文献[1]用广义的雅可比椭圆函数展开法研究了方程(1),获得了许多行波解,在文献[2]中,利用平面动力系统分支理论,讨论了各种参数状态下行波解的存在性;当α=β=γ=δ=1时,文献[3-5]对其解进行了研究;当α=C20,β=0时,文献[6]利用雅可比椭圆函数展开法对其解进行研究;当α=1,β=1,γ=-3,δ=1时,文献[7]利用广田法对其解进行了研究.

最近,由文献[8]提出了(G′/G)-展开法,并成功地获得了一些非线性演化方程的精确解.大量学者用该方法求解了大量的非线性偏微分方程(组)的精确解,之后出现了许多改进的(G′/G)-展开法[9],广义的(G′/G)-展开法[10]等,本文将利用改进的G′/G-展开法研究广义的(2+1)维Boussinesq方程,从而得到了方程(1)与目前现有文献不同的新精确解.

2 广义的(2+1)维Boussinesq方程的精确解

3 结论

本文利用改进的(G′/G)-展开法,获得了广义的(2+1)维Boussinesq方程的用双曲函数、三角函数和有理函数表示的精确解,其中当双曲函数表示的行波解中参数取特殊值时,便得到广义的(2+1)维Boussinesq方程的孤立波解,本文拓展了原来的(G′/G)-展开法,丰富了广义的(2+1)维Boussinesq方程的解,从求解的过程可以看出,该方法在求解非线性微分方程精确解时具有更直接、更简洁的特点,此法也可以推广到求其他非线性微分方程的精确解.

参考文献

[1]Chen H T, Zhang H Q. New double periodic and multiple soliton solutions of the generalized (2+1)-dimensional Boussinesq equation[J]. Chaos Solitons Fract, 2004,20(4):756-769.

[2]Song M, Shao S G. Exact solitary wave solutions of the generalized (2+1) dimensional Boussinesq equation[J].Applied Mathematics and Computation, 2010,217:3557-3563.

[3] El-Sayed S M, Kaya D. The decomposition method for solving (2+1)-dimensional Boussinesq equation and (3+1)-dimensional KP equation[J]. Appl. Math. Comput, 2004,157(2):523-534.

[4] Abdel Rady A S, Osman E S, Khalfallah M. On soliton solutions of the (2+1) dimensional Boussinesq equation[J]. Appl. Math. Comput., 2009,(5):28.

[5] Chen Y, Yan Z Y, Zhang H Q. New explicit solitary wave solutions for (2+1)-dimensional Boussinesq equation and (3+1)-dimensional KP equation[J]. Phys. Lett. A., 2003,307(2/3):107-113.

[6] Liu S K, Fu Z T, Liu S D, et al. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Phys. Lett. A, 2001,289(1/2):69-74.

[7] Johnson R S. A two-dimensional Boussinesq equation for water waves and some of its solutions[J]. J. Fluid Mech., 1996,323:65-78.

[8] Wang M L.The(G′/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J]. Physics Letters A, 2008,372(4):417-423.

[9] Guo S M, Zhou Y B, Zhao C X. The improved (G′=G)-expansion method and its applications to the Broer- Kaup equations and approximate long water wave equations[J]. Applied Mathematics and Computation,2010, 216:1965-1971.

[10] Zhang S,Wang W,Tong J L.A generalized(G′/G)-expansion method and its application to the (2+1)-dimensional Broer-Kaup equations[J]. Applied Mathematics and Computation, 2009,209:399-404.

Application of the improved(G′/G)-expansion method to exact solutions for generalized (2+1)-dimensional Boussinesq equation

Zhao Yunmei1,Yang Yun jie2,Jiang Yan3
(1. Department of Mathematics, Honghe University, Mengzi 66110, China; 2. Department of Mathematics, Kunming University, Kunming 650031, China; 3. Department of Mathematics, Simao Teachers′ College, Puer 665000, China)

In this paper,the im proved(G′/G)-expansion method is used to construct exact solutions of the generalized(2+1)-dimensional Boussinesq equation.As a resu lt,some new travelling wave solutions involving parameters,exp ressed by three typesof functionswhich are the hyperbolic functions,the trigonometric functions and the rational functions,are obtained.When the param eters are taken as special values,the solitary wave solutions are derived from the hyperbolic function solutions.

generalized(2+1)dimensional Boussinesq equation,homogeneous balance, im p roved(G′/G)-expansion method,exact solution

O175.2

A

1008-5513(2012)02-0176-05

2011-11-03.

国家自然科学基金(11161020);云南省科技厅项目(2011FZ193);昆明学院校级项目(XJ11L021).

赵云梅(1972-),硕士,副教授,研究方向：偏微分方程.

2010 MSC:35Q58,37K 50