局部环上幂等矩阵线性组合广义逆之间的关系

吴炎

(琼州学院理工学院,海南 三亚 572022)

局部环上幂等矩阵线性组合广义逆之间的关系

吴炎

(琼州学院理工学院,海南 三亚 572022)

设R是2为单位的局部环.研究了R上三个两两可换的n阶非零幂等矩阵的线性组合广义逆之间的包含关系,确定了R上一类特殊矩阵广义逆的列表算法.利用这种列表算法和相关的矩阵理论,得到了这些矩阵线性组合广义逆之间的包含关系的充要条件,推广了矩阵自反广义逆的逆反律的相关结果.

局部环;关系;矩阵广义逆;列表算法;矩阵线性组合

1 引言和与预备知识

矩阵广义逆相关问题的研究,在统计学等诸多领域中有着较好的应用.关于矩阵广义逆的逆反律、拓展等相关问题,文献[1-6]已给出了一些有意义的结果.文献[7]在数域上研究并给出了三个幂等矩阵线性组合的可逆性条件,而文献[1-3]研究了域上矩阵积的广义逆及其自反广义逆的逆反律,得到了(AB){1}⊂B{1}A{1},B{1,2}A{1,2}⊂(AB){1,2}等成立的一些条件.受此启发,本文从另一角度,通过确定局部环R上一类特殊矩阵广义逆的列表算法,研究R上三个两两可换的n阶非零幂等矩阵线性组合广义逆之间的包含关系,得到了3个幂等矩阵线性组合的广义逆之间包含关系(aA1+bA2+cA3){1}⊂(aA1){1}+(bA2){1}+(cA3){1}), (aA1+bA2+cA3){1,3}⊂(aA1){1,3}+(bA2){1,3}+cA3{1,3}等成立的充要条件,拓展了上述矩阵广义逆的相关研究,其中a,b,c∈R.

2 一类特殊矩阵广义逆的列表算法

表1 一类特殊矩阵广义逆的列表算法

3 幂等矩阵线性组合的广义逆之间的关系

本节将利用特殊矩阵广义逆的列表算法,在局部环上讨论几个幂等矩阵线性组合广义逆与这些幂等矩阵的纯量乘积矩阵的广义逆之间的包含关系.

以下证明,在上述16种可能情形中,当a,b,c∈R*且a+b+c=0时的8种情形中只有一种存在.而当a,b,c∈R*且a+b+c/=0时的另8种中,只有七种情形存在.依次讨论如下:

若有a,b,c∈R*且a+b+c=0时,而选取a+b,a+c,b+c中至少有一个元为零.譬如设a+b=0,则由a+b+c=0得到c=0与已知条件矛盾;对于a+b,a+c,b+c中a+c=0和b+c=0,或其中至少有两个元素为零的情形,都得到类似的矛盾.故a,b,c∈R*且a+b+c=0时,只有a+b,a+c,b+c∈R*成立,即1)存在.

若a,b,c∈R*且a+b+c/=0时,而选取a+b=a+c=b+c=0,则有a=b=c,且由a+b=0和a=b得到2a=0,而2是R的单位,故有a=0与题设条件矛盾.因此当a,b,c∈R*且a+b+c/=0时,只有上面2)至8)共七种情形存在.故(i)得证.

(ii)在假设条件下,由(i)及(aA1+bA2+cA3){1}/=∅,就有条件1)-8)之一成立.在这些条件中,无论何种情形都有a,b,c∈R*,故由(20)-(22)式及定理2.1(i)得

其次,在所设条件下,由于有条件2)-8)之一成立.此时无论2)-8)的哪个条件成立, aA1+bA2+cA3的标准形(23)式中均有a,b,c,a+b+c∈R*,且a+b,a+c,b+c中每一个元只能取可逆元或零,都适合定理2.1(i)和(ii)条件,故可由定理2.1(ii)中列表算法得到, (aA1+bA2+cA3){1}中任一元素可表为:

对于2)-8)中任何一种情形,由于(24)式成立,故对由(31)式所表示的(aA1+bA2+cA3){1}中任一元F,都有F=F1+F2+F3,其中F1,F2,F3分别是形如(26)-(28)的一个取定的矩阵.因此比较(31)、(26)、(27)、(28)式中右边矩阵的(1,1)位置元,就有(25)式成立.

证明(i)必要性由定理3.1得到,下面再证明充分性.

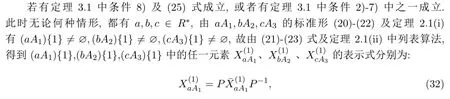
以下要证(24)式成立,只证(43)式中任一取定矩阵fiW可表为:fiW=W1+W2+W3即可,其中W1,W2,W3分别是形如(33)、(35)、(37)式的一个取定矩阵.通过比较(33)、(35)、(37)和(43)式中的对应位置元素易见,在一形如(43)式的矩阵fiW被取定后,可按(33)、(35)、(37)式中元素的以下取法,来确定形如(33)、(35)、(37)式的各自一个取定矩阵W1,W2,W3:

II)(33)、(35)、(37)式中非对角线上元的选取:

当(43)式中元Xij=0(i/=j;i,j=1.2,…,8)时,在(33)、(35)、(37)的矩阵中相应位置上,选取Hij=Yij=Zij=0(i/=j;i,j=1.2,…,8)(Hij,Yij,Zij中已为0的,就保持不变).

当(43)式中元Xij/=0(i/=j;i,j=1.2,…,8)时,由于(33)、(35)、(37)中矩阵的相同位置元Hij,Yij,Zij(i,j=1,2,…,8)中至少有一个为任意选取的矩阵,若有Hij,Yij,Zij(i/= j;i,j=1.2,…,8)中Yij(或Hij或Zij)为任选矩阵,则选取Yij(或Hij或Zij)等于Xij,而其余两个均取0(若已经是0,就保持不变).

依上法选取W1=(Hij),W2=(Yij),W3=(Zij)中元素后,就使得由(43)式所表示的(aA1+bA2+cA3){1}中任一取定元fiW能表成fiW=W1+W2+W3,也即保证(24)式成立.

(ii)用定理2.1(iii)及引理3.1,用类似定理3.1及(i)的方法可证明之.用推论3.1及类似以上方法还可以得到如下较为整齐的结果:

[1] Shinozaki N, Sibuya M. Further results on the reverse order law [J]. Linear Algebra Appl., 1979,27:9-16.

[2] Pierro De A R, Wei Musheng. Reverse order law for re°exive generalized inverse of products of matrices[J].Linear Algebra Appl., 1998,277:299-311.

[3]刘淑丹,游宏.域上矩阵积的广义逆及自反广义逆的逆反律[J].数学年刊:A辑,2004,25(4):523-530.

[4]吴炎.Galois环上特殊矩阵的分类及其应用[M].北京:科学出版社,2006.

[5]吴炎,张宗杰,符晓芳.局部环上矩阵广义逆半群的子集及其性质[J].数学的实践和认识,2011,41(6):168-174.

[6]吴炎,邱发儒,易文静.相似变换下方阵的拓展I-逆及其应用[J].河南大学学报:自然科学版,2010,40(6):565-570.

[7]张俊敏,成立花,李祚.幂等矩阵线性组合的可逆性[J].纯粹数学与应用数学,2007,23(2):231-235.

The relationship between generalized inverse of linear combinations of idempotent matrices over a local ring

Wu Yan

(School of Physics and Engineering, Qiongzhou University, Sanya 572022, China)

Let R be a local ring with 2 is an unit. In this paper, the inclusion relation of the generalized inverse of linear combinations of three nonzero n times n idempotent matrices which are mutually commutative are studied over a local ring R, and the tabulation algorithm for the generalized inverse of a class special matrix are given. Moreover,by using the tabulation algorithm and the relative matrix theory , the necessary and su±cient conditions of inclusion relationships about the generalized inverse of linear combinations of these matrices are obtained, and the relative theory of reverse order law for re°exive generalized inverse of matrix are also generalized.

local ring, relationship, generalized inverse of matrices, the tabulation algorithm, linear combinations of matrices

O151.21

A

1008-5513(2012)02-0155-12

2011-11-14.

海南省自然科学基金(109005);三亚市基金(SY 11036).

吴炎(1964-),教授,研究方向：矩阵与矩阵群及其应用.

2010 MSC:15A 09