二进小波的构造方法研究
2012-07-05吐尔洪江阿布都克力木阿布都许库热阿布都克力木张海英
吐尔洪江·阿布都克力木,阿布都许库热·阿布都克力木,张海英
(1.新疆师范大学数学科学学院,新疆 乌鲁木齐 830054;2.新疆博乐市第七中学,新疆 博乐 833400; 3.新疆工业高等专科学校电气与信息工程系,新疆 乌鲁木齐 830091)
二进小波的构造方法研究
吐尔洪江·阿布都克力木1,阿布都许库热·阿布都克力木2,张海英3
(1.新疆师范大学数学科学学院,新疆 乌鲁木齐 830054;2.新疆博乐市第七中学,新疆 博乐 833400; 3.新疆工业高等专科学校电气与信息工程系,新疆 乌鲁木齐 830091)
提出两种二进小波的构造方法.首先,将Mallat构造的B-样条二进小波推广得到一种构造B-样条二进小波的新方法;其次,基于二进提升方案提出构造二进小波的另一种新方法—–构造定理,并通过调整定理中提升参数的形式、以新的B-样条二进小波作为初始二进小波,具体构造了具有有限长单位脉冲响应、高阶消失矩、线性相位的提升二进小波,这些提升二进小波不能由Sweldens提升方案得到.
二进提升方案;消失矩;二进小波滤波器
1 引言
小波分析作为一种新的有效地图像处理工具已备受关注,与此同时,许多小波的构造方法也被提出.本文提出两种二进小波的构造方法:第一种,通过引入参数,将M allat构造的B-样条二进小波[1]推广得到一种构造B-样条二进小波的新方法;第二种,Sweldens提升方案仅局限于双正交小波的构造[23],对于构造二进小波,这种提升方案无能为力.二进提升方案克服了Sweldens提升方案的局限性,此方案从二进小波出发构造新的二进小波[45]或双正交小波[6],本文基于二进提升方案提出了构造二进小波的一种新方法—–构造定理,用于构造具有高阶消失矩的提升二进小波,并且具体构造了有限长单位脉冲响应、高阶消失矩、线性相位的提升二进小波,而这些提升二进小波却不能由Sweldens提升方案得到.
2 二进小波的构造
定义2.1若
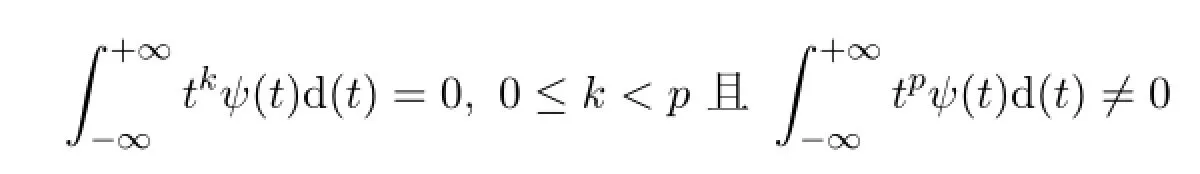
成立,则称ψ(t)为p阶消失矩小波.

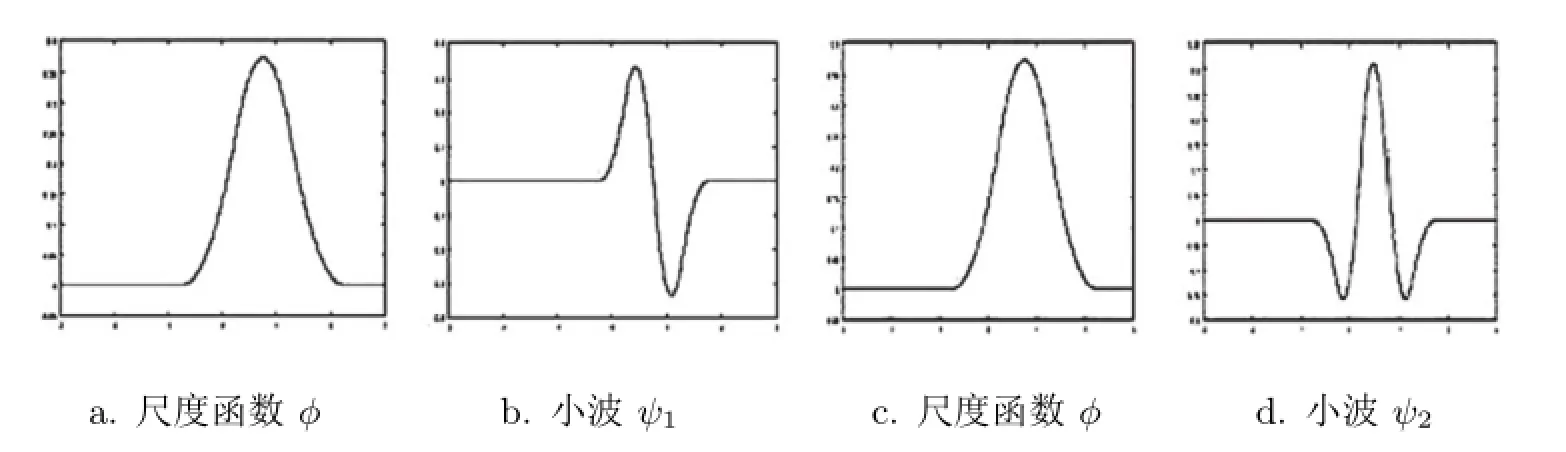
图1 尺度函数φ(t)与小波ψr(t)的图像(r=1,r=2)
2.2 提升二进小波的构造
2.2.1 构造定理
下面提出二进提升方案,此方案以二进小波滤波器作为初始滤波器,用于构造二进小波滤波器或双正交小波滤波器.
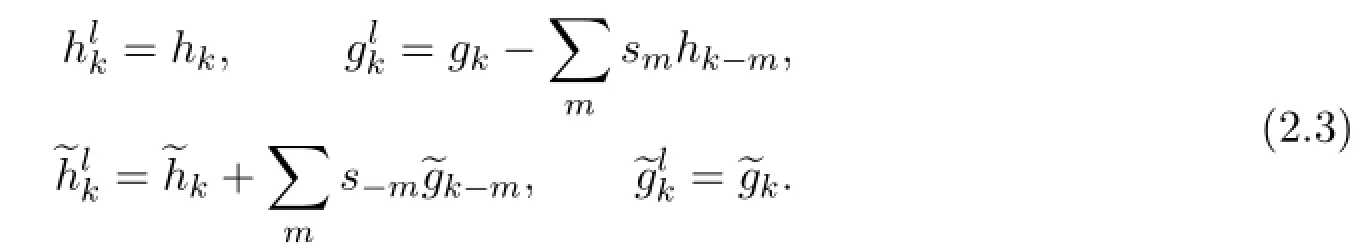
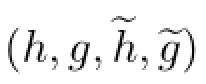
下面的推论说明Sweldens提升方案是二进提升方案的特例,双正交小波空间是二进小波空间的子空间.
推论2.1若滤波器是双正交小波滤波器,在(2.3)式中取s2m+1=0,则(2.3)式为Sweldens提升方案.
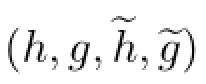
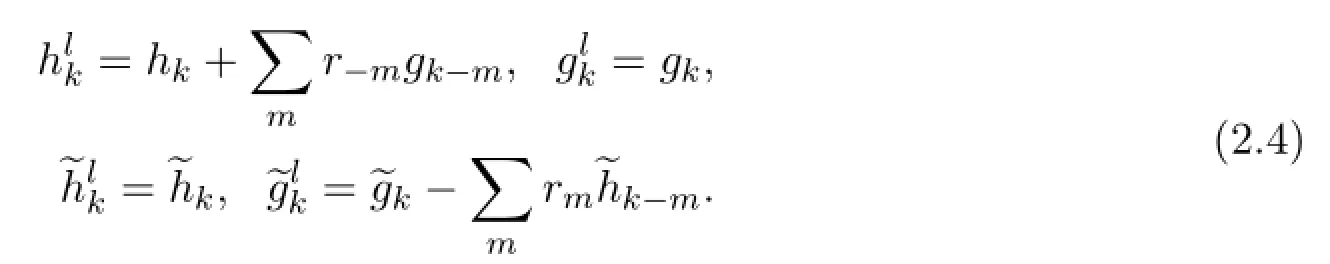
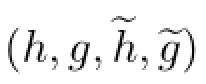
基于二进提升方案,提出如下两个构造定理,运用这两个定理,通过调整提升参数的形式,能够构造具有高阶消失矩的提升二进小波滤波器.

2.2.2 高阶消失矩的提升二进小波的构造
选取某二进小波滤波器作为初始二进小波滤波器,利用定理2.1、定理2.2,构造具有更高阶消失矩的提升二进小波滤波器.本节以2.2.1构造的新的B-样条二进小波滤波器(以r=1,m=2的滤波器为例)作为初始二进小波滤波器.
r=1,m=2的滤波器中g具有1阶消失矩.应用定理2.1,考虑到紧支撑和线性相位的要求,选取适当的提升参数,构造有2阶或更高阶消失矩的滤波器gl.此时,b s(ω)满足条件:

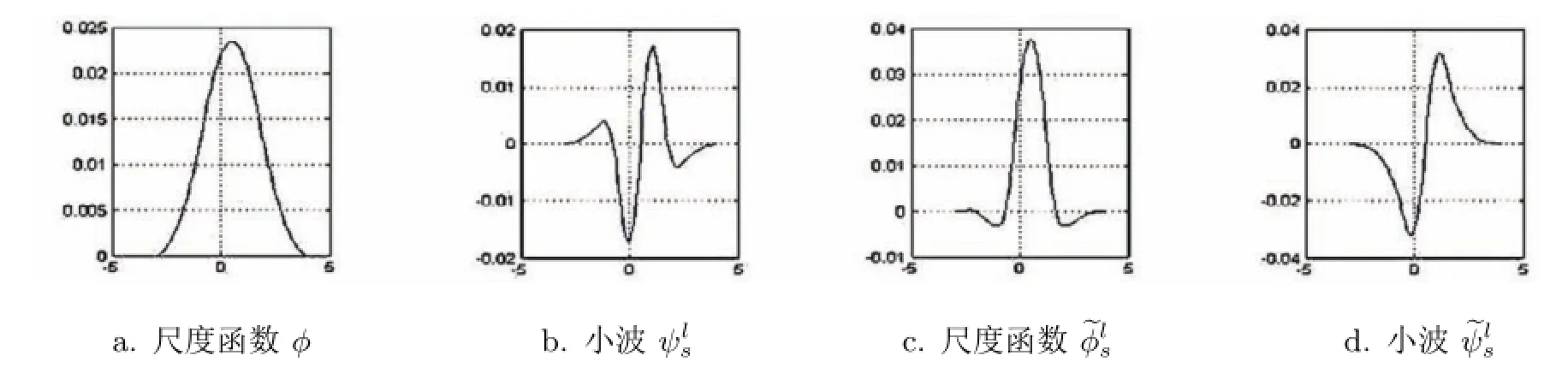
图2 两个尺度函数和小波()的图像

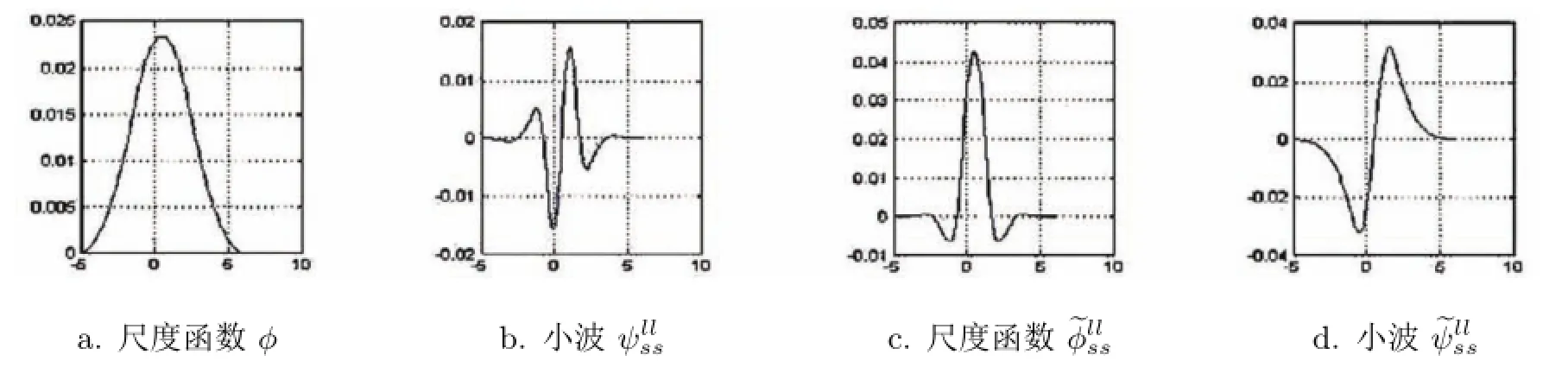
图3 两个尺度函数和小波(φ,ψllss,~φllss,~ψllss)的图像

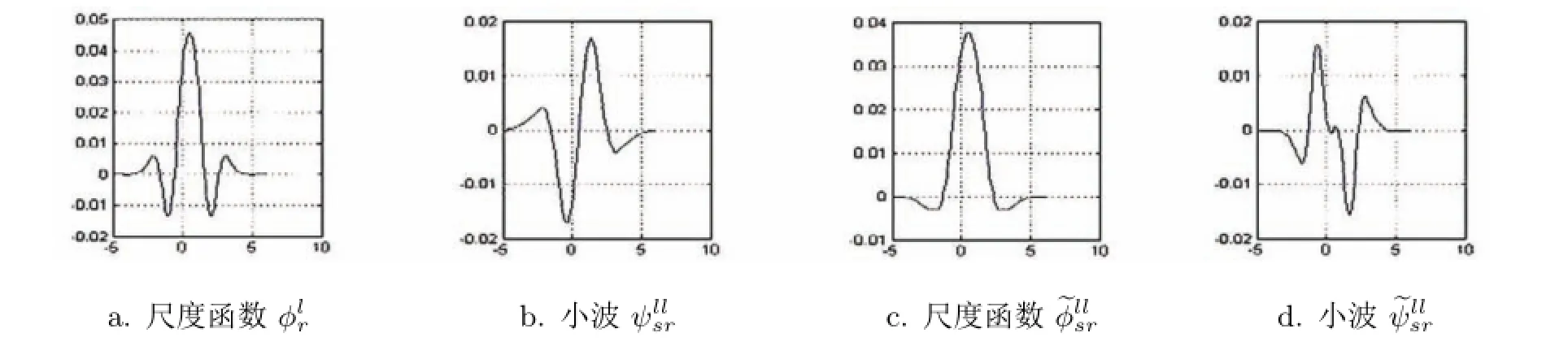
图4 两个尺度函数和小波(φlr,ψllsr,~φllsr,~ψllsr)的图像
此提升过程也适用于r=1,m=1,3,…与r=2,m=1,2,…的B-样条二进小波滤波器.所以从二进小波滤波器出发应用定理2.1、定理2.2,选取适当的提升参数可以构造满足实际需要的各种特性的二进小波滤波器.
3 结论
本文先后提出两种构造二进小波的方法:第一种,通过引入参数,将Mallat构造的B-样条二进小波推广得到新的B-样条二进小波;第二种,在二进提升方案的基础上,基于消失矩条件提出了两个构造定理,用于构造具有高阶消失矩的二进小波滤波器,并且从r=1,m=2的二进小波滤波器出发具体构造了具有有限长单位脉冲响应、高阶消失矩、线性相位的二进小波滤波器.鉴于二进小波变换的平移不变性的特点和本文构造的二进小波滤波器所具有的优点,将其应用于图像增强、边缘检测和特征提取等方面或许会取得更好的图像处理效果.
[1] Mallat S. A Wavelet Tour of Signal Processing[M]. NewYork: Academic Press, 1998.
[2] Sweldens W. The lifting scheme: A construction of second generation wavelets[J]. SIAM J. of Math. Anal.,1997,29(2):511-546.
[3] Sweldens W. The lifting scheme: A custom-design construction of biothogonal wavelets[J]. Appl. Comput. Harmon. Anal., 1996,3(2):186-200.
[4] Turghunjan Abdukirim, Aireti Abulikemu, Taxpulat Eziz. Lifting Dyadic wavelets and design of decom-position filters with short length[J]. IEEE International Conference on Computer Science and Automation Engineering, 2011,1:517-520.
[5] Abdukirim T, Hussain M, Niijima K, et al. The dyadic lifting schemes and the de-noising of digital image[J].International Journal of Wavelets,Multi-resolution and Information Processing, 2008,6(2):331-351.
[6] Abdukirim T, Niijima K, Takano S. Design of biorthogonal wavelet filters using dyadic lifting scheme[J]. Bulletin of Informatics and Cybernetics, 2005,37:123-136.
Study on new construction methods of dyadic wavelet filters
Turghunjan Abdukirim1,Abduxukur Abdukirim2,Zhang Haiying3
(1. School of Mathematical Sciences, Xinjiang Normal University, Urumqi 830054, China;2. Xinjiang Bortala No.7 High School, Bortala 833400, China;3. Electrical and Information Engineering Department, Xinjiang Ploytechnical College, Urumqi 830091, China)
In this paper, we study on two new construction methods of dyadic wavelet filters. One method isthat new B-spline dyadic wavelet filters are obtained by generated B-spline dyadic wavelet filters proposed by Mallat. Other is that two theorems for constructing lifting dyadic wavelet filters with higher number of vanishing moments are proposed based on the dyadic lifting schemes. Meantime we design lifting dyadic wavelet filters with finite impulse response, higher number of vanishing moments and linear phase according to new B-spline dyadic wavelet filters .These lifting filters can not be obtained by Sweldens lifting scheme.
dyadic wavelets, dyadic lifting scheme, vanishing moments
O235
A
1008-5513(2012)02-0149-06
2011-08-01.
国家自然科学基金(10661010);新疆维吾尔自治区自然科学基金(200721104).
吐尔洪江·阿布都克力木(1962-),博士,教授,研究方向:小波分析、数字图像与模式识别.
2010 MSC:94A 15
