带不定权非线性边界的p-Lap lacian问题解的存在性

杨菲菲,章国庆

(上海理工大学理学院,上海 200093)

带不定权非线性边界的p-Lap lacian问题解的存在性

杨菲菲,章国庆

(上海理工大学理学院,上海 200093)

研究了一类带不定权非线性边界的p-Laplacian椭圆方程.获得了当非线性边界的特征值参数小于第二特征值时,该方程存在非平凡解.主要工具为环绕定理.

环绕定理;非线性边界;p-Lap lacian问题

1 引言

为Steklov问题[1].文献[2]证明了问题(1.2)存在一列特征值序列λk→+∞,且其对应的特征函数构成Sobolev空间W1,2(Ω)中的一组完备规范正交基.当p/=2时,文献[3]研究如下特征值问题:

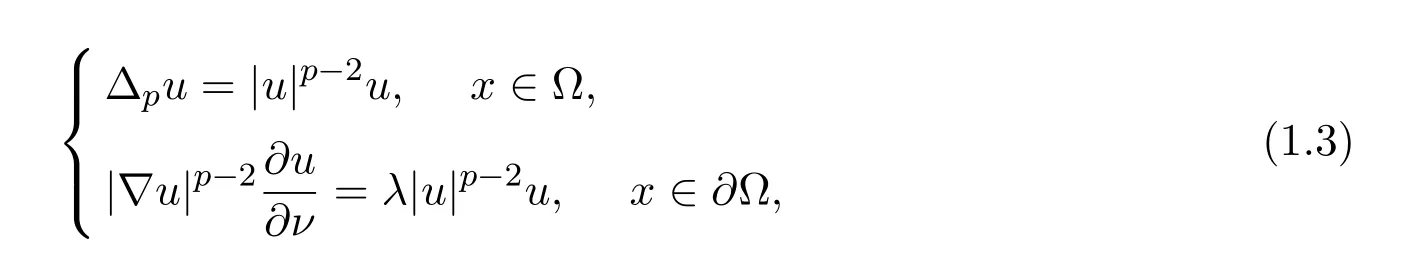
利用L-S临界点定理,证明了问题(1.3)存在变分特征值序列λk→+∞,但是,并不清楚其对应的特征函数是否构成W1,2(Ω)中的一组完备规范基.这给利用环绕定理来讨论带非线性边界的p-Lap lacian问题带来了本质困难.1998年,文献[4]建立了一种新的环绕定理,并研究了

证明了当λ＜λ2时(为第二特征值),问题(1.4)非平凡解的存在性.

本文利用一类带不定权非线性边界的p-Lap lacian特征值问题第二特征值性质以及文献[4]提出的环绕定理,证明了当特征值参数λ小于其第二特征值时,问题(1.1)存在非平凡解.

2 预备知识和主要定理

证明了问题(2.4)的第一特征值λ1的单重性,孤立性,以及所对应的特征函数的不变号性,以及存在一列趋向于无穷大的特征值λk→+∞,同时也证明了第二特征值为

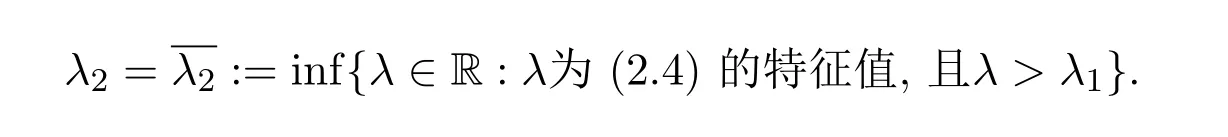
据特征值问题(2.4)的第一特征值和第二特征值的性质,类似文献[4]中的推论2.1,可得:

3 定理2.3的证明

由V(x)满足条件(*)和(H1),可得E(u)∈C1(W1,p;ℝ),则问题(1.1)的弱解即为泛函E(u)的临界点,由条件(H2)易知,0是问题(1.1)的平凡解.

[1]Steklov MW.Sur les p roblemes fondamentaux de la physique mathematique[J].Ann.Sci.Ecole Norm. Sup.,1902,19:455-490.

[2]Auchmuty G.Steklov eigenproblem s and rep resentation of solutions of elliptic boundary value p roblem s[J]. Num er.Funct.Anal.Optim.,2004,25:321-348.

[3]Bonder JF,Rossi JD.Existence results for the p-Lap lacian with nonlinear boundary conditions[J].J.Math. Anal.App l.,2001,263:195-223.

[4]Fan X L,Li Z C.Linking and existence results for perturbations of the p-Lap lacion[J].Nonlinear Anal., 2000,42:1413-1420.

[5]Bonder J F,Rossi J D.A nonlinear eigenvalue problem with indefinite weights related to the Sobolev trace embedding[J].Publ.Mat.,2002,46:221-235.

[6]Xuan B J.Variational Methods:Theory and App lication[M].Hefei:University of Science and Technology of China Press,2006.

[7]Brezis H,Lieb E.A relation between pointw ise convergence of functions and convergence of functionals[J]. Proc.Amer.Math.Soc.,1983,88:486-490.

Existence result for the p-Laplacian problem with nonlinear boundary cond itions

Yang Feifei,Zhang Guoqing
(College of Sciences,University of Shanghai for Science and Technology,Shanghai 200093,China)

In this paper,we consider a class of p-Lap lacian elliptic equation with indefinite weights nonlinear boundary condition.The existence of nontrivial solutions for the equation is obtained when the eigenvalue param eter of the indefinite weight is less than the second eigenvalue.Them ain tool is the linking argum ent.

linking argum ent,non linear boundary condition,p-Lap lacian prob lem

O175.25

A

1008-5513(2012)03-0412-06

2011-05-25.

上海市自然科学基金(11ZR 1424500);上海市重点学科建设项目(S30501).

杨菲菲(1985-),硕士生,研究方向：非线性分析及其应用.

2010 MSC:35J60,47J30