不含5-圈的平面图的无圈边着色

吴燕青,谢德政,赵灿鸟

(1.山西师范大学数学系,山西临汾 041000;2.重庆大学数学与统计学院,重庆 401331)

不含5-圈的平面图的无圈边着色

吴燕青1,2,谢德政2,赵灿鸟2

(1.山西师范大学数学系,山西临汾 041000;2.重庆大学数学与统计学院,重庆 401331)

图G的一个无圈边着色是一个正常的边着色且不含双色的圈.图G的无圈边色数是图G的无圈边着色中所用色数的最小者.本文用反证法得到了不含5-圈的平面图G的无圈边色数的一个上界.

无圈边着色;无圈边色数;平面图

1 引言

本文所考虑的图都是有限简单图.文中未加定义的术语和记号看文献[1].如果图G的一个顶点的度为k(至少为k),称它为G的一个k-顶点(k+-顶点).如果一个图G的一个面的度为3,称它为三角形.一个图G的正常边着色是一个映射φ:E(G)→{1,…,k},使得对每一对相邻的边e1和e2,有φ(e1)/=φ(e2).一个正常的边着色φ被称为是无圈的,如果着色φ中不存在双色的圈.设c:E(G)→{1,…,k}是G的一个无圈边着色,且C={1,…,k}.图G的无圈边色数是G的无圈边着色中所用色数的最小者,用(G)表示.如果一个图G能用k种颜色对它进行无圈边着色,那么称这种着色为G的无圈边k-着色.

2001年,文献[2]提出了无圈边着色猜想(简称AECC):对于任意的图G,有

2 主要结论

如果d(f)=4,那么w′(f)=w(f)=0.如果d(f)≥6.根据(R1),显然w′(f)≥0.

因此,对于x∈V(G)∪F(G),有w′(x)≥0.引理1.1成立.

为了叙述方便,给出以下定义和记号.关于G的一个部分着色c,颜色α∈C对于某条边e称为是候选的,如果e的邻没有被着颜色α.我们用Rc(e)表示在着色c下由边e的候选颜色组成的集合.关于G的一个部分着色c,如果一条路上所着的颜色是由α,β交替出现的最长路,称这条路为(α,β)-最长路.如果一条(α,β)-最长路且它的起点v关联的边和终点u关联的边所着色的颜色都是α,则称这条路为(α,β,vu)-关键路.对uv∈E(G),C(v)表示与顶点v相关联的边在着色c下所着的颜色组成的集合.c(uv)表示uv在着色c下所着的颜色.设Cuv=C(v)-c(uv).如果一个集合S的任何元素在这个集合中可以出现多次并且计算它的元素个数时按重数计算,称S为多重集(multiset)[5].对于x∈S,用DS(x)表示x在多重集S中出现的次数,用‖S‖表示S的元素个数.设S和S′是两个多重集,如果一个多重集S⊎S′包含S与S′中的所有元素且对于x∈S⊎S′,称之为S和S′的并.

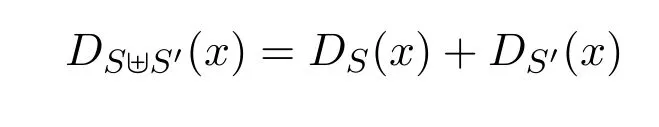
引理1.2[3]假设颜色α和β是图G的一个正常边着色c中的任意两种不同的颜色,那么G中最多有一条(α,β)-最长路包含某一顶点v.

引理1.3[3]设u,i,j,a,b∈V(G),ui,uj,ab∈E(G)且{λ,ξ}⊆C,使得

在G的一个部分无圈着色c下,假设存在一条(λ,ξ,ab)-关键路包含顶点u，着色c′是在c下交换边ui和uj的颜色而其它边的颜色保持不变得到的.如果c′是一个正常的边着色,那么图G在c′下就不再存在任何的(λ,ξ,ab)-关键路.

定理1.1假设图G是一个不含5-圈的平面图,那么χ′a(G)≤Δ(G)+4.

证明假设不成立.设G是含边数最少的一个反例.显然G是连通的且δ(G)≥2.根据引理1.1,G至少包含(A1)-(A3)中的一种结构.设k=Δ(G)+4.设颜色集C为:

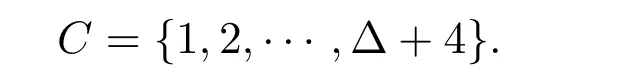
情形1G包含一个3-顶点v,设{v1,v2,v3}=NG(v),其中

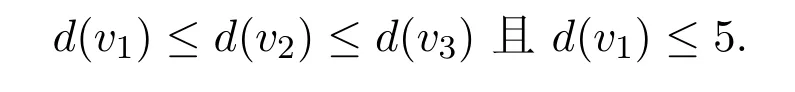
设H=G-vv1,由G的最小性,H有一个无圈边着色c用了k种颜色.假设d(v1)=5.

情形1.1|C(v)∩C(v1)|=0.

由于

所以存在一种颜色α∈C-C(v)∪C(v1),用它给边vv1着色而其它边的颜色保持不变得到着色c′.显然c′是G的一个无圈边k-着色,矛盾.

情形1.2|C(v)∩C(v1)|=1.

设v′1是v1在H中的一个邻,不失一般性,假设c(vv3)=c(v1v′1)=1,c(vv2)=2.不妨设C(v1)={1,3,4,5}.则

否则vv1可着{6,7,…,Δ+4}中的一种颜色而其它边的颜色保持不变得到G的一个无圈边k-着色.此时vv3着3,v1v′1着2和vv1着1而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.

情形1.3

不妨设C(v1)={1,2,3,4}.则{5,6,…,Δ+4}中有一种颜色不在C(v3)中,不妨设5/∈C(v3),用5给vv1着而其它边的颜色保持不变得到G的一个着色c′.如果c′是G的一个无圈边k-着色,矛盾.否则,存在一条(1,5,vv1)-关键路关于着色c.现在重新着vv3用5而其它边的颜色保持不变得到着色c′,根据引理1.2,不再有(1,5,vv3)-关键路关于着色c′.显然着色c′是H的一个无圈边k-着色,正如情形1.2,矛盾.

设ui∈NH(v1),其中i=1,2,3.设Sv是一个多重集且Sv=Cvv2⊎Cvv3⊎Cvv4.

情形2.1|C(v)∩C(v1)|=0.

由于|C(v)∪C(v1)|≤3+Δ(G)-1＜k,所以存在α∈C-C(v)∪C(v1),用它给边vv1着色而其它边的颜色保持不变得到着色c′,显然c′是G的一个无圈边k-着色,矛盾.

情形2.2|C(v)∩C(v1)|=1.

不失一般性,假设c(vv4)=c(v1u1)=1.c(vv2)=2,c(vv3)=3.不妨设C(v1)={1,4,5}.则

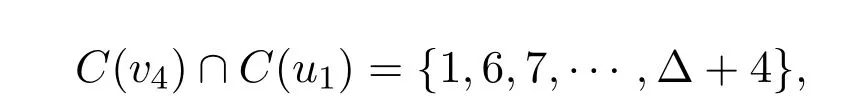
否则vv1可着{6,7,…,Δ+4}中的一种颜色而其它边的颜色保持不变得到G的一个无圈边k-着色.此时vv4着4,v1u1着2和vv1着1而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.

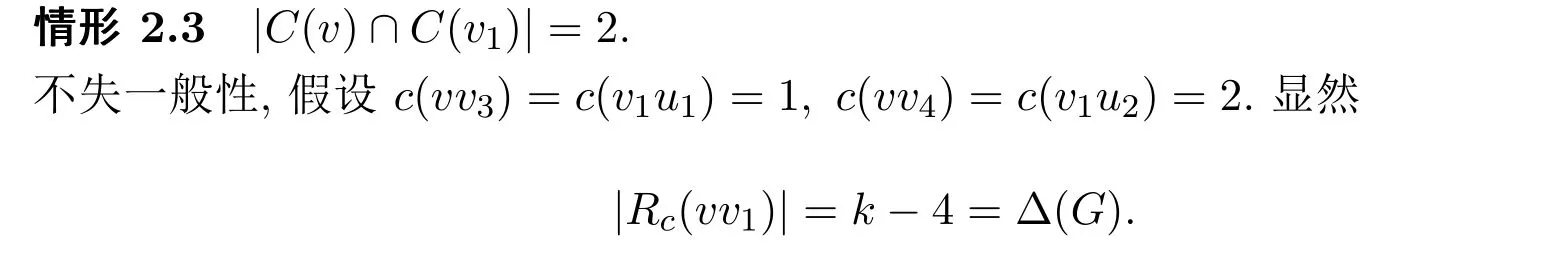
如果存在α∈Rc(vv1),用它给边vv1着色而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.否则,存在一条(1,α,vv1)-关键路或(2,α,vv1)-关键路关于着色c.如果在C(v)中至少有两种颜色在Sv中.由于

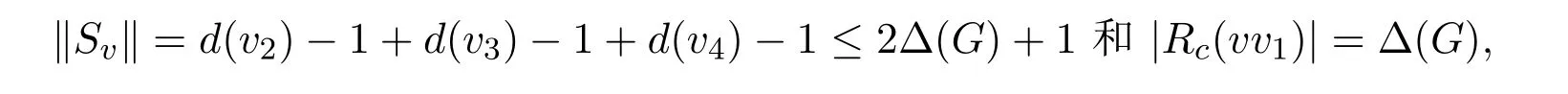
因此存在γ∈Rc(vv1)在Sv中出现恰好一次.假设γ∈C(v3),现在用γ给vv4重新着色而其它边的颜色保持不变得到着色c′,如果c′是H的一个无圈边着色,那么|C′(v)∩C′(v1)|=1.这种情况前面已讨论,矛盾.如果着色c′不是H的一个无圈边着色,显然c′是H的一个正常的边着色且存在一条(1,γ,vv4)-关键路关于着色c.但还存在(1,γ,vv1)-关键路关于着色c,根据引理1.2,矛盾.如果C(v)中至多有一种颜色在Sv中.假设c(vv4)∈Sv.现在交换边vv2和vv3的颜色而其它边的颜色保持不变得到着色c′,显然c′是H的一个无圈边着色.设C1表示由边vv1的候选颜色组成的集合使得它们中的任何一种颜色给边vv1着和颜色1形成关键路.C2与C1类似.根据引理1.3,对于α∈C1不会再存在一条(1,α,vv1)-关键路关于着色c′.如果存在α∈C1,用它给边vv1着色而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.否则,C1⊂C′vv4.因而(C1∪C2)⊂C′vv4,但是|C1∪C2|=Δ(G),这与|C′vv4|≤Δ(G)-1矛盾.

不妨设c(vv2)=1,c(vv3)=2,c(vv4)=3.显然|Rc(vv1)|=k-3=Δ(G)+1.如果存在α∈Rc(vv1),用它给边vv1着色而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.否则,存在一条(1,α,vv1)-关键路或(2,α,vv1)-关键路或(3,α,vv1)-关键路关于着色c.由于‖Sv‖=d(v2)-1+d(v3)-1+d(v4)-1≤2Δ(G)+1,显然存在一种颜色α∈Rc(vv1)在Sv中恰好出现一次.假设α∈C(v4).现在用颜色α给边vv3重新着色而其它边的颜色保持不变得到着色c′.如果c′是H的一个无圈边着色,那么|C′(v)∩C′(v1)|=2,这种情形前面已讨论,矛盾.如果c′不是H的一个无圈边着色,显然c′是H的一个正常的边着色且存在一条(3,α,vv3)-关键路关于着色c,但是,关于着色c还存在一条(3,α,vv1)-关键路,根据引理1.2,矛盾.

下面假设G不包含结构(A 2)和(A 3),根据引理1,那么G一定包含结构(A 1).

情形3G包含一个2-顶点v,设{v1,v2}=NG(v),其中d(v1)≤d(v2).

现在把G的所有2-顶点删掉得到图G′.不失一般性,假设δ(G′)≥2.根据引理1.1,那么G′一定包含(A1)-(A3)中的一种结构,也就是说存在顶点v′∈V(G′),它在G中不满足(A 1)-(A 3)中的任何一种结构,而在G′中满足(A 1)-(A 3)中的一种.设

设u是M中度最小的一个顶点.显然,dG′(u)≤5.设N′(u)={x|x∈NG(u),dG(x)=2}, N′′(u)=NG(u)-N′(u).显然N′′(u)=NG′(u).根据对u的选择,|N′(u)|/=0,因此存在u′∈N′(u).设NG(u′)={u,u′′}且H=G-{uu′}.根据对G的选择,H有一个无圈边k-着色c.设B′(u)={c(ux)|x∈N′(u)},B′′(u)={c(ux)|x∈N′′(u)}.

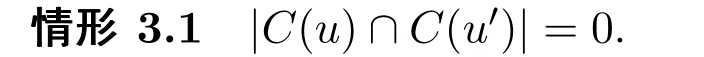
由于|C-C(u)∪C(u′)|≥k-(Δ(G)-1+1)=4,所以存在α∈C-C(u)∪C(u′),用它给边uu′着色而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.

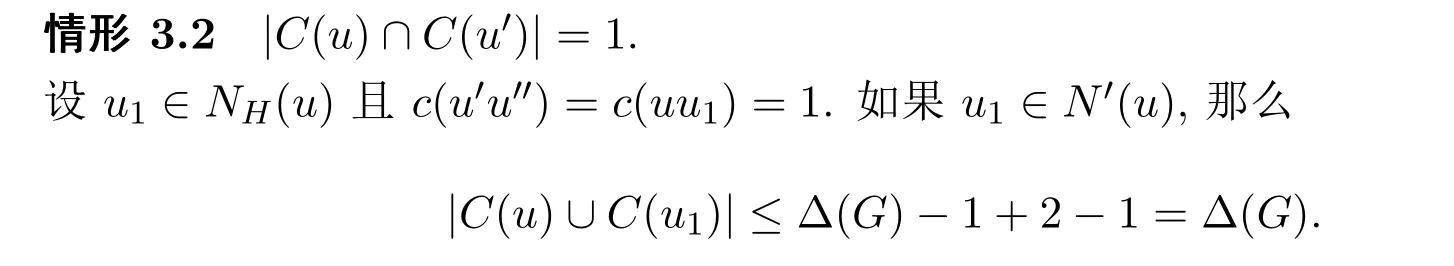
因此存在α∈C-C(u)∪C(u1),用它给边uu′着色其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.如果u1∈N′′(u),下面分两种情况来讨论.

(1)如果dG′(u)≤4,由于

所以存在α∈C-B′′(u)∪C(u′′),用它给边u′u′′重新着色而其它边的颜色保持不变得到着色c′.显然c′是H的一个无圈边着色.如果|C′(u)∩C′(u′)|=0,这种情形前面已讨论,矛盾.

如果|C′(u)∩C′(u′)|=1,那么一定存在一个2-顶点u2∈NH(u)且c′(uu2)=c′(u′u′′).这种情形前面已讨论,矛盾.

(2)如果dG′(u)=5,那么一定存在一个3-顶点y,它与u相邻并且在G中不与2-顶点相邻(在G中不含(A2),而在G′中含(A2)).如果u1=y,由于

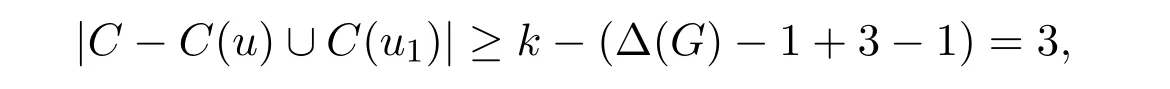
因此存在α∈C-C(u)∪C(u1),用它给边uu′着色而其它边的颜色保持不变得到G的一个无圈边k-着色,矛盾.如果u1/=y,由于

所以存在α∈C-C(u′′)∪B′′(u)c(uy),用它给边u′u′′重新着色而其它边的颜色保持不变得到着色c′.显然c′是H的一个无圈边着色.如果|C′(u)∩C′(u′)|=0,这种情形前面已讨论,矛盾.如果|C′(u)∩C′(u′)|=1,那么一定存在一个2-顶点u2∈NH(u)且c′(uu2)=c′(u′u′′)或者c′(u′u′′)=c′(uy).这种情形前面已讨论,矛盾.

[1]Bondy J A,Murty U SR.Graph Theory with App licattion[M].New York:Macm illan Press,1976.

[2]A lon N,Sudakov B,Zaks A.Acyclic edge colorings of graphs[J].J.Graph Theory,2001,37:157-167.

[3]Basavaraju M,Sunil Chand ran L.Acyclic edge coloring of graphs with m aximum degree 4[J].J.Graph Theory,2009,61:192-209.

[4]Hou J,Wu J,Liu G,et al.Acyclic edge colorings of p lanar graphs and series-parallel graphs[J].Science in China Series A:Mathem atics,2009(3):605-616.

[5]Basavara ju M,Sunil Chandran L.Acyclic edge coloring of p lanar graphs[J].SIAMJ.Discrete Math., 2011,25:463-478.

[6]Dong W,Xu B.Some resu lts on acyclic edge colorings of p lanar graphs[J].Information Processing Letters, 2010,110:887-892.

[7]Borow ieckiM,Fiedorow icz A.Acyclic edge coloring of p lanar graphswithout short cycles[J].Discrete Math., 2010,310:1445-1455.

A cyclic edge coloring of planar graphs without 5-cycles

Wu Yanqing1,2,Xie Dezheng2,Zhao Canniao2
(1.Departm ent of Mathem atics,Shanxi Norm al University,Lin fen 041000,China; 2.College of Mathem atics and Statistics,Chongqing University,Chongqing 401331,China)

An acyclic edge coloring of a graph Gis a proper edge coloring such that there are no bichrom atic cycles.The acyclic edge chromatic number of a graph Gis the least number of colors in an acyclic edge coloring of G.In this paper,an upper bound on the acyclic edge chrom atic number for p lanar graphs without 5-cycles was obtained using p roof of contradiction.

acyclic edge coloring,acyclic edge chromatic number,p lanar graph

O157.5

A

1008-5513(2012)03-0342-07

2010-10-22.

吴燕青(1982-),硕士,助教,研究方向：图论及其应用.

2010 MSC:05C15