具脉冲效应的非自治随机干扰的捕食-食饵系统的研究
2012-07-05谭德君
谭德君
(集美大学教师教育学院,福建厦门 361021)
具脉冲效应的非自治随机干扰的捕食-食饵系统的研究
谭德君
(集美大学教师教育学院,福建厦门 361021)
建立一个具有脉冲效应的非自治随机的比例依赖的捕食-食饵模型,通过研究具有脉冲效应的非自治随机系统与无脉冲效应的非自治随机系统的等价性,证明该模型的有界性,均值一致有界和灭绝性等动力学性质.
脉冲效应;随机扰动;捕食-食饵系统;有界性
1 引言
捕食-食饵系统是一个重要的生态系统,有许多学者对此进行深入研究,得到许多结论[1-2],具有比例依赖功能反应的捕食-食饵系统也得到广泛的研究[3-4].生物种群生活在不断变化的环境中,如:季节的变化,食物供给等,人类的活动,环境的突然变化,如:洪水、地震、海啸时种群产生瞬间的影响,环境的噪音对种群的发展产生不断的影响,所以研究脉冲效应[5-6]和随机环境[7-8]的非自治种群动力学行为,成为现代生物数学的一个主要课题,但是考虑脉冲与环境噪音同时对生态种群作用的成果不多.本文借鉴文献[2,9]的方法,利用具有脉冲效应的非自治随机系统与无脉冲效应的非自治随机系统的等价性,研究具有脉冲效应和随机扰动的非自治捕食-食饵系统的动力学性质.
本文研究具有脉冲效应的非自治随机的与比例依赖功能反应的捕食-食饵系统.
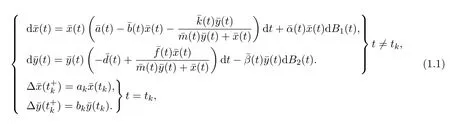

2 主要结果







3 结论
本文给出了具有脉冲扰动和比例依赖功能反应的非自治随机捕食-食饵系统,首先建立一个脉冲扰动和无脉冲扰动的比例依赖功能性反应的非自治随机捕食-食饵系统的平衡关系;其次,利用这种关系通过对无脉冲非自治的随机捕食-食饵系统的研究,得到有脉冲非自治的随机捕食-食饵系统的动力学性质.这种对具有脉冲扰动和随机扰动的生态种群研究的方法是一种特殊的方法,更一般的方法有待进一步研究.
[1]Aziz-A laoui MMA,Daher Okiye M.Boundedness and global stability for a predator-prey model with m odified Leslied Gower and Holling type 2 schem es[J].App l.Math.Lett.,2003,16:1069-1075.
[2]张树文,张耘嘉,谭德君.具脉冲效应和Beddington-DeAnglis功能反应时滞周期捕食系统[J].纯粹数学与应用数学,2010,4:534-540.
[3]Hsa B S,Hwang T W,Kuang Y.Global analysis of the Michaelis-Menten ratio-dependent p redator-p rey system[J].Math.Biol.,2001,42:489-506.
[4]Xu R R,Chen L S.Persistence and global stability for n-species ratio-dependent p redator-p rey system with tim e delay[J].Math.Anal.App l.,2002,275:27-43.
[5]Liu B,Teng Z D,Chen L S.Analysis of predator-prey m odelwith Holling 2 functional response concerning im pu lsive control strategy[J].Com put.App l.Math.,2006,193:347-362.
[6]Nie L L,Teng Z D,Hu L.Existence and stability of periodic solution of a predator-prey m odel state dependent im pulsive affects[J].Com put.App l.Math.,2009,224:544-555.
[7]Jiang D D,Shi N,Li X.Global stability and stochastic perm anence of non-autonom ous logistic equation with random perturbation[J].Math.Anal.App l.,2008,340:588-597.
[8]Ji C J,Jiang D J,Li X Y.Qualitative analysis of a stochastic ratio-dependent predator-prey system[J]. Journal of Com putational and App lied Mathematics.,2011,235:1326-1341.
[9]Li C X.Si J P,Jiang S.Stability of im pu lsive stochastic differential delay system s and its app lication to im pu lsive stochastic neural networks[J].Nonlinear Analysis,2011:74:3099-3111.
[10]K lebaner F F.Introdution to Stochastic Calculus with App lication[M].London:Im perial College Press, 1998.
Study of non-autonom ous predator-prey system with impulsive effects and random perturbation
Tan Dejun
(College of Education of Teacher,Jimei University,Xiamen 361021,China)
A m odel of a non-autonom ous ratio-dependent p redator-p rey system with im pulsive effects and random perturbation is builded.The equivalent relation between the solution of non-autonom ous stochastic differential system with im pu lsive effects and that of a corresponding non autonomous stochastic differential system with im pulsive effect is researched.Moreover,we prove som e dynam ic behavior of this system for the boundedness,uniform ly bounded in them ean and extinction of this system.
im pu lsive effect,random perturbation,predator-prey system,boundedness
0231
A
1008-5513(2012)03-0285-09
2012-02-02.
福建省自然科学基金(2008J0199).
谭德君(1965-),硕士,教授,研究方向:生物数学.
2010 MSC:34D 05,34D 20
