具有多参数的奇摄动非线性边值问题的摄动解

李超,王晓云

(1.中北大学理学院,山西太原 030051;2.山西警官高等专科学校基础部,山西太原 030021)

具有多参数的奇摄动非线性边值问题的摄动解

李超1,王晓云2

(1.中北大学理学院,山西太原 030051;2.山西警官高等专科学校基础部,山西太原 030021)

讨论含多个参数的高阶非线性方程的摄动解,在适当的条件下,先构造出外部解,再根据不同的边界层,利用伸展变量和幂级数展开式理论,构造问题的形式渐近解,最后利用微分不等式理论证明渐近解的一致有效性和渐近形态,把奇摄动非线性问题中的参数推广到多个参数.

非线性;多参数;奇摄动;边值问题;边界层校正

1 引言

对于含小参数非线性系统(奇摄动非线性系统)边界层研究一直是众多致力于非线性系统工作者非常关注的问题[1-6].近几十年来,处理奇摄动非线性系统边界层的很多方法已经陆续被提出,并不断被优化.其中一些经典的方法有边界层法、匹配渐近展开法、多重尺度法等.另外,一些学者还利用微分不等式方法来研究奇摄动非线性系统,如文献[7-15]利用微分不定式等方法研究了奇摄动非线性常微分方程边值问题、反应扩散方程、椭圆型方程边值问题、奇摄动问题的激波层解和大气物理问题等.文献[16]利用微分不等式研究了两个参数的非线性方程的奇摄动解.本文在文献[16]的基础上,讨论了一类具有n个参数的非线性奇摄动边值问题,并证明了解的一致有效性.

考虑如下非线性奇摄动边值问题:

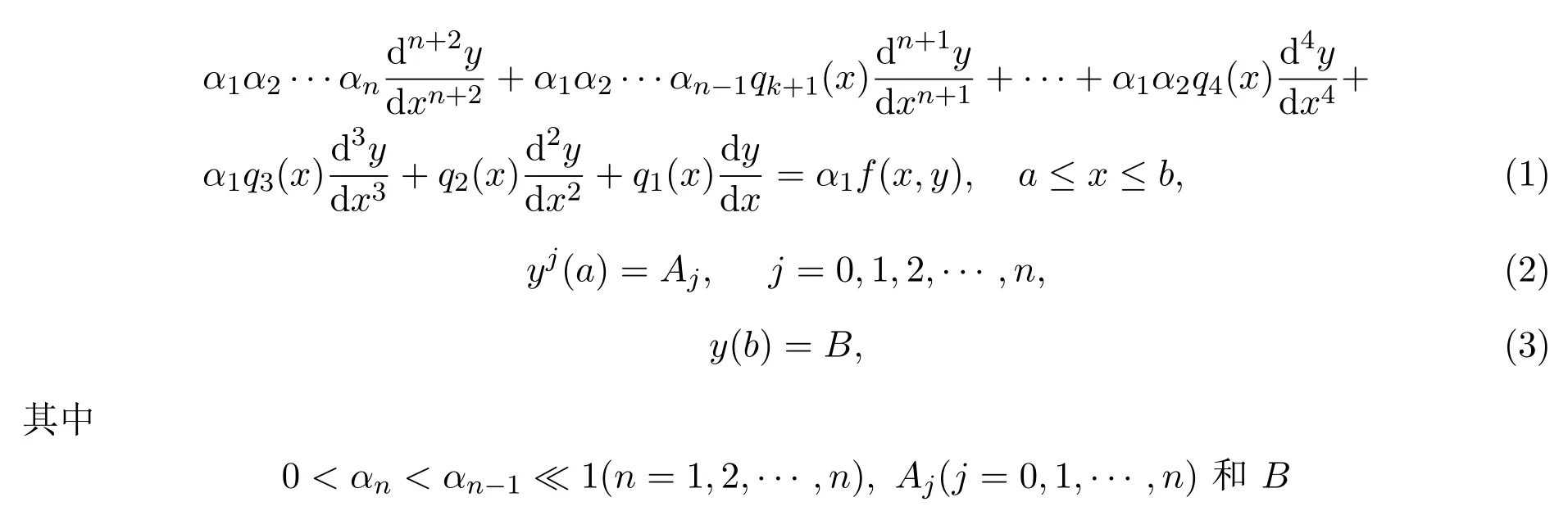
为常数.为了方便,此处把(1)-(3)式记为系统(N).

2 方程的形式渐近解

2.1 外部解

依次可求得

显然,由(9)式得到的解Y0就是退化问题(4)-(5)的解Y0(x),且由(10)式可以依次地得到Yi,这样就得到外部解

但是它并不满足j=1,2,…,n时的边界条件,所以需要构造在x=a附近的第一,第二,…,第n边界层校正项.

2.2 第一边界层校正

为了得到系统(N)形式渐近解的一致有效展开式,下面在不同的边界层引入伸长不同的变量来构造函数.

定义1.1中间方程:方程(1)某一系数趋于零时得到的方程称为中间方程.

现考虑(6)式的中间方程

2.3 第二边界层校正

2.4 第n边界层校正

3 解的一致有效性证明

[1]De Jager EduardusMarie,Jiang Furu.The Theory of Singular Perturbation[M].Am sterdam:North-Holland Publishing Co.,1996.

[2]NiWeim ing,Wei Juncheng.On positive solution concentrating on spheres for the Gierer-Meinhard t system[J].Journal of Differential Equations,2006,221(1):158-189.

[3]Zhang Fu.Coexistence of a pulse and mu ltip le spikes and transition layers in the standing waves of a reation-diffusion system[J].Journal of D ifferential Equations,2004,205(1):77-155.

[4]Khasm inskii Refail Zalmannovich,Yin George.Lim it behavior of two-time-scale diffusion revisited[J]. Journal of D ifferential Equations,2005,212(1):85-113.

[5]Marques Iim a.Existence and asym p totic behavior of solutions for a class of nonlinear ellip tic equationswith Neum ann condition[J].Non linear Analysis,2005,61(1):21-40.

[6]Bobkova A S.The behavior of solutionsmu ltidim ensional singu larly perturbed system with one fast variable[J].Journal of Differential Equations,2005,41(1):23-32.

[7]Mo Jiaqi.A singularly perturbed non linear boundary value p roblem[J].Journal of Mathem atical Analysis and App lications,1993,178(1):289-293.

[8]Mo Jiaqi.Singular perturbation for a class of nonlinear reaction diffusion system[J].Science in China:Ser. A,1989,32(11):1306-1315.

[9]莫嘉琪,朱江.非线性非局部反应扩散方程奇摄动问题[J].应用数学和力学,2003,24(5):446-470.

[10]莫嘉琪,王辉,林万涛.一类具有边界摄动的非线性非局部反应扩散方程奇摄动问题[J].应用数学和力学, 2005,26(12):1507-1510.

[11]Mo Jiaqi.The singu larly perturbed boundary value problem s for higher-order sem ilinear elliptic equation[J]. Advances in Mathem atics,2001,30(2):141-148.

[12]莫嘉琪,王辉.一类非线性激波问题位置的转移[J].应用数学和力学,2005,26(1):53-57.

[13]Mo Jiaqi,Lin Wantao,Zhu Jiang.A variational iteration solvingmethod for ENSO mecham ism[J].Progress in Natural Science,2004,14(12):1126-1128.

[14]Mo Jiaqi,Wang Hui,Lin Wantao,et al.Sea-air oscillator model for Pacific SST[J].Acta Phys Sinica, 2006,55(1):6-9.

[15]Mo Jiaqi,Wang Hui,Lin Wantao,et al.Varitional iterationmethod themechanism of the equatorialeastern Pacific EINino-Southern oscillator[J].Chinese Physics,2006,55(4):671-675.

[16]陈丽华,莫嘉琪.具有双参数的非线性方程的奇摄动解[J].应用数学和力学,2007,28(10):1197-1202.

[17]O′Malley Robert Emm ett.introduction to Singu lar[M].New York:Academ ic Press,1974．

Singu larly perturbed solution for nonlinear equations with some parameters

Li Chao1,Wang Xiaoyun1,2
(1.College of Science,North University of China,Taiyuan 030051,China; 2.Departm ent of Mathem atics,Shanxi Police Academ y,Taiyuan 030021,China)

A class of nonlinear speed system perturbed solution non local prob lem is discussed in this paper.In approp riate conditions,first constructed out external solution,again according to different boundary layer and using stretchy variable and power series launched theory,the asym ptotic expansions of solution of this p roblem is shown and p roved to be uniform ly effective using the theory of differential inequality in the whole interval. This paper extends the perturbed problem of the parameters of the parameters of the p romotion to multip le param eters.

nonlinear,m any param eters,singularly perturbed,boundary value prob lem, boundary layer correction

O178

A

1008-5513(2012)03-0370-08

2012-01-23.

山西省自然科学基金(2011011002-1);中国博士后科学基金(20100471857).

李超(1987-),硕士生,研究方向：应用数学.

2010 MSC:15A 42