广义Ekeland变分原理的应用
2012-07-05万轩赵克全
万轩,赵克全
(重庆师范大学数学学院,重庆 400047)
广义Ekeland变分原理的应用
万轩,赵克全
(重庆师范大学数学学院,重庆 400047)
研究了广义Ekeland变分原理在拟度量空间中的一些重要应用.利用广义Ekeland变分原理证明了函数f满足关于α的Takahashiε-条件当且仅当f满足关于相同α的Hamelε-条件.此外,利用关于α的Takahashiε-条件得到了一些重要结论.
广义Ekeland变分原理;拟度量空间;Takahashiε-条件;Hemalε-条件
1 引言
众所周知,自文献[1-2]在1972年给出关于带扰动的下半连续函数取严格极小值的变分原理以来,由于其在最优化、控制论和非线性分析等领域有着广泛的应用,出现了许多Ekeland变分原理的推广形式和等价形式的研究[3-10].特别地,文献[3]在概率度量空间中证明了Ekeland变分原理与Caristi不动点定理等价.文献[4]在完备度量空间中研究了一般Ekelandε-变分原理以及它的Borwein-Preiss光滑ε-变分原理的一些应用.文献[5]在完备度量空间中利用Ekeland变分原理证明了Takahashiε-条件的等价定理,以及在弱尖极小及不动点等中的应用.文献[7]在完备度量空间中证明了广义Ekeland变分原理,并利用其推导出广义Caristi不动点定理,广义Takahashi非凸最小化定理,非凸极小极大定理以及非凸平衡定理等相关给论.文献[9]在拟度量空间上建立了具有Q-函数的Ekeland变分原理,并证明了多值映射下的Caristi-K irk型不动点定理、Takahashi定理与其等价和一些相关给论.
本文在完备拟度量空间下建立Takahashiε-条件及Hemalε-条件,并利用Ekeland变分原理证明其等价性及一些相关结论.
2 预备知识
为了得到本文的主要结果,首先引进下面的定义和引理.
定义2.1[9]设X为非空集合.映射d:X×X→ℝ+使得对任意的x,y,z∈X满足: (M1)d(x,y)≥0;(M2)d(x,y)=0当且仅当x=y;(M3)d(x,y)≤d(x,z)+d(z,y),则称映射d是X上的拟度量,(X,d)称为拟度量空间.
定义2.2[9]映射q:X×X→ℝ+满足:
(Q1)∀x,y,z∈X,q(x,y)≤q(x,z)+q(z,y);
(Q2)如果x∈X和序列{yn}n∈ℕ⊆X,存在M=M(x)>0使得q(x,yn)≤M和limn→∞yn=y(关于拟度量),则q(x,y)≤M;
(Q3)对任意的ε>0,存在δ>0使得q(x,y)≤δ和q(x,z)≤δ蕴含d(y,z)≤ε,则称映射q为Q-函数.
定义2.3[11]称函数f:X→ℝ∪{+∞}为从上面下半连续(简记:lsca),如果对任意序列{xn}n∈ℕ⊆X收敛于某一点x∈X和对任意n∈ℕ满足f(xn+1)≤f(xn),有

根据文献[5],下面给出在拟度量空间上的关于α的Takahashiε-条件和关于α的Hamel ε-条件的定义.设

定义2.4设(X,d)为拟度量空间,q:X×X→ℝ+为Q-函数,φ:(-∞,∞]→(0,∞)为非减函数和f:X→ℝ∪{+∞}为有下界的真lsca.
函数f满足关于α的Takahashiε-条件,如果存在α>0,0<ε≤+∞和对任意满足infXf<f(x)<infXf+ε的x∈X,则存在y∈X,y/=x,使得

函数f满足关于α的Hamelε-条件,如果存在α>0,0<ε≤+∞和对任意满足infXf<f(x)<infXf+ε的x∈X,则存在z∈Z,使得
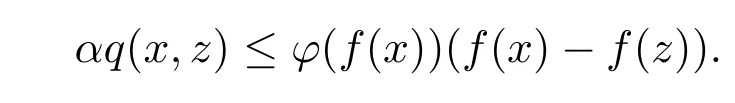
特别地,当ε=+∞时,则关于α的Takahashiε-条件和Hamelε-条件分别叫做关于α的Takahashi件和Hamel条件.
引理2.1设(X,d)为拟度量空间,q:X×X→ℝ+为Q-函数,φ:(-∞,∞]→(0,∞)为非减函数和f:X→ℝ∪{+∞}为有下界真lsca.则对任意的0<ε1<ε2,关于α的Takahashi ε2-条件蕴含关于相同α的Takahashiε1-条件和关于α的Hamelε2-条件蕴含关于相同α的Hamelε1-条件.
证明对α>0,0<ε1<ε2≤+∞和对任意满足infXf<f(x)<infXf+ε1的x∈X,则对这些任意的x∈X也满足infXf<f(x)<infXf+ε2,再利用f满足关于α的Takahashi ε2-条件,则存在y∈X,y/=x,使得
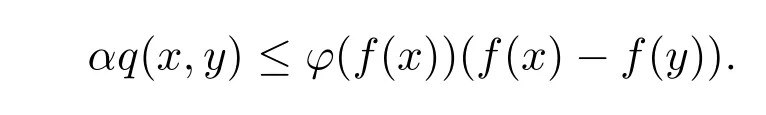
即f满足关于相同α的Takahashiε1-条件.
同理可得,关于α的Hamelε2-条件蕴含关于相同α的Hamelε1-条件.

3 主要结果




[1]Ekeland I.Sur lesprobemesvariationnels[J].Com ptesRendusde l′Acadˊem iedes Sciences-Series I,1972,275: 1057-1059.
[2]Ekeland I.On the variational princip le[J].Journal of Mathematical Analysis and App lication,1974,47:324-353.
[3]Zhang Shisheng,Chen Yuqing,Guo Jinli.Ekeland′s variational princip le and Caristi′s fixed point theorem in p robabilistic m etric space[J].Acta.Mathem eticae App licatae Sinica,1991,7(3):217-228.
[4]Li Yongxin,Shi Shuzhong.A generalization of Ekeland′sε-variational p rincip le and its Borwein-Preiss sm ooth variant[J].Journal of Mathem atical Analysis and App lications,2000,246:308-319.
[5]Wu Zili.Equivalent formu lations of Ekeland′s variational princip le[J].Nonlinear Analysis,2003,55:609-615. [6]Monica Bianchi,Gˊabor Kassay,Rita Pini.Existence of equilibria via Ekeland′s princip le[J].Journal of Mathem atical Analysis and App lications,2005,305:502-512.
[7]Lin Laijiu,Du W S.Ekeland′s variational princip le,m inimax theorem sand existence of nonconvex equilibria in com p letem etric spaces[J].Journal of Mathem atical Analysis and App lications,2006,323:360-370.
[8]Lin Laijiu,Du W S.Some equivalent formu lations of the generalized Ekeland′s variational p rincip le and their app lications[J].Non linear Analysis,2007,67:187-199.
[9]A l-Hom idan S,Ansari Q H,Yao J C.Some generalizations of Ekeland-type variational princip le with app lications to equilibrium problem s and fixed point theory[J].Nonlinear Analysis,2008,69:126-139.
[10]Xiang Shuwen,Yin Wenshuang,Wang Changchun.Some new resu lts on stability of Ekeland′sε-variational p rincip le[J].Journal of Mathem atical Analysis and App lications,2008,339:802-810.
[11]Chen Yuqing,Cho Y J,Yang Li.Note on the resu lts with lower sem i-continuity[J].Bu lletin of the Korean Mathem atical Society,2002,39(4):535-541.
Applications of generalized Ekeland′s variational principle
Wan Xuan,Zhao Kequan
(Department of Mathematics,Chongqing Normal University,Chongqing 400047,China)
In this paper,some im portant app lications about generalized Ekeland′s variational p rincip le in quasi-m etric space are investigated.We proved that function f satisfies theε-condition of Takahashi with αiff f satisfies theε-condition of Hamel with the sameαby the generalized Ekeland′s variational princip le. Furtherm ore,som e im portant conclusions are obtained by theε-condition of Takahashiwithα.
generalized Ekeland′s variational princip le,quasi-m etric space,theε-condition of Takahashi, theε-condition of Hamel
O176;O177.91
A
1008-5513(2012)03-0363-07
2011-06-02.
国家自然科学基金(10831009);重庆市科委运筹学与系统工程重点实验室专项经费(CSTC,2011KLORSE02);重庆自然科学基金(2011BA 0030);重庆市教委科技项目(KJ110625).
万轩(1987-),硕士生,研究方向:变分分析及应用研究.
2010 MSC:65K 10
