具有脉冲种间偏利关系的Lotka-Volterra模型的稳定性分析
2012-07-05石金喜窦霁虹邵彩宏
石金喜,窦霁虹,邵彩宏
(1.西北大学数学系,陕西西安 710127;2.通辽市第一中学,内蒙古通辽 028000)
具有脉冲种间偏利关系的Lotka-Volterra模型的稳定性分析
石金喜1,窦霁虹1,邵彩宏2
(1.西北大学数学系,陕西西安 710127;2.通辽市第一中学,内蒙古通辽 028000)
通过对具有偏利关系的病虫害种群的研究,建立了具有固定时刻脉冲的偏利关系系统,并构造频闪映射,利用Jury判定证明了该系统解的最终有界性及平衡点的稳定性,并结合理论上的结果给出了防治病虫害方面的一些建议.
偏利关系模型;脉冲;频闪映射;Jury判据;稳定性
1 引言
现实生活中的许多生物种群生长都呈现出脉冲效应,因此用脉冲微分方程描述这些现象更切合实际、更科学.比如使用杀虫剂进行捕杀害虫,本文通过对具有偏利关系的害虫种群(如沙棘木蠹蛾和红缘天牛),建立了有固定时刻脉冲的偏利关系系统.
首先,种群间的偏利共生关系,是指种间的相互作用仅对一方有利(偏利),而对另一方没有影响的种群间的关系.
两种群相互作用的Lotka-Volterra模型[1]的一般形式如下:
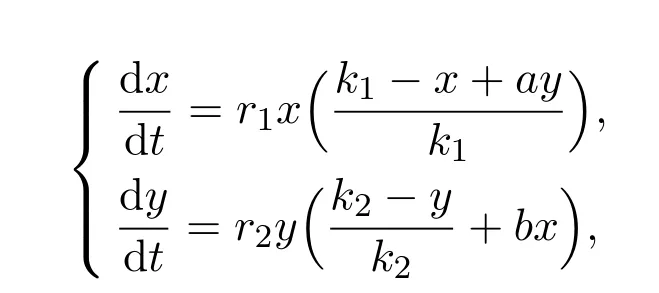
则偏利共生关系下的Lotka-Volterra模型为:

其中x≥0,y≥0,r1>0,r1>0,k1>0.k2>0,a>0.
r1,r2分别代表种群x,y的内禀增长率;k1,ak2+k1分别代表种群x,y的环境最大容纳量;a>0代表种群x受益,种群y不受影响.
其次,传统的Lotka-Volterra偏利共生关系模型常假定种群的发展是连续的,而事实上由于外界瞬间的影响使得其间断,也就产生脉冲.本文考虑了一类具有脉冲的种间偏利共生关系的Lotka-Volterra系统,更符合实际.
最后,基于以上及利用文献[2]得到本文研究的具有固定脉冲收获的偏利关系模型如下:
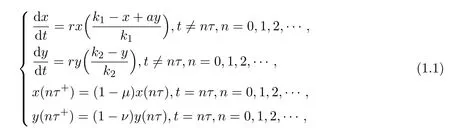
其中,r,k1,k2,a,µ,ν均为正常数,且µ,ν均小于1,系统(1.1)的解

上连续,而且
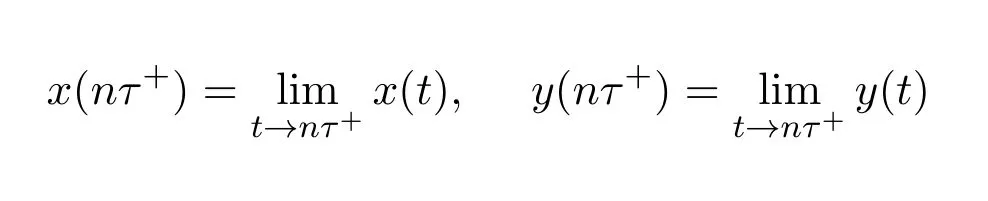
存在.
2模型求解
在任意一个脉冲区间(nτ,(n+1)τ]内结合系统(1.1)中的第二个方程对满足系统(1.1)中的y(t)进行求解得:

3 解的最终有界性
依据参考文献[3-4]的证明思路,得到以下两个定理.
定理3.1设(x(t),y(t))T是系统(1.1)的解,且x(0+)>0,则当0<µ<1,0<ν<1时,对所有的t≥0有x(t)≥0,y(t)≥0.进一步,若t>0,则x(t)>0,y(t)>0.
定理3.2当0<µ<1,0<ν<1时,脉冲动力系统(1.1)的每个解(x(t),y(t))T是最终有界的.
证明首先证明系统(1.1)中y(t)的最终有界性.
由系统(1.1)考虑可以得到:
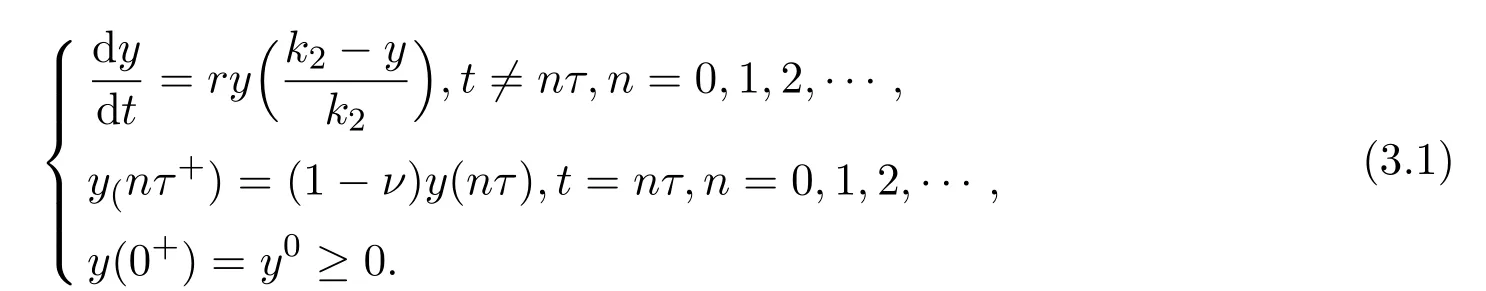
若t/=nτ+,一旦y(t)≥k2,则y′(t)≤0.即对足够大的t/=nτ+,y(t)≤k2.
若t=nτ+,则由(2.1)知,在每个连续脉冲中,有
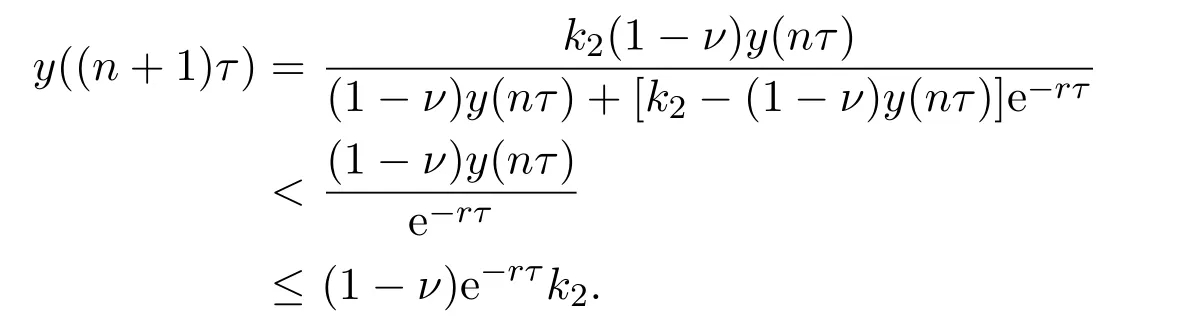
于是y(nτ+)总不会超过正常数(1-ν)e-rτk2.由以上证明可得y(t)是最终有界的,且若规定M2=max(k2,(1-ν)e-rτk2),则对于足够大的t有y(t)≤M2.
下面证明x(t)的最终有界性.

那么,由以上证明和V(t)的定义及y(t)的最终有界性可得到x(t)也是最终有界的,证毕.
4 模型平衡点及稳定性
首先,利用(2.3)式以及模型(1.1)的后两个方程,得到频闪映射(脉冲时刻的种群数量递推关系)如下:


由于(4.2.2)中后两个式子均大于0,而只要当n充分大时(4.2.2)中的第三个式子就可以大于0,所以所以由Jury条件知:只要(4.2.2)中第一个式子也大于0,则E1也稳定,又因为当n充分大时,当ν>1-e-rτ时(4.2.2)中第一个式子也大于零.
即当ν>1-e-rτ时,E1是稳定的,否则不稳定,证毕.
5 结论分析
自然界中有许多变化规律都呈现初脉冲效应,比如,在农业生产中的对害虫的治理,使用杀虫剂进行治理害虫.对于本文,可以将其利用到具有偏利共生关系的害虫(如沙棘木蠹蛾和红缘天牛)的治理中,联系本文以上的结论可以发现,随着杀虫剂的长期使用,只要药量足够,这两种害虫种群的发展趋势[6-7]只有两种:
(1)对应E1的稳定性,种群x逐渐消失,而种群y的数量逐渐达到固定值;
(2)对应E0的稳定性,两种害虫逐渐消失.本文没有考虑杀虫剂对捕食者的影响,对于广谱性杀虫剂,它不仅仅杀害害虫,同时也会误杀天敌,对于广谱性杀虫剂产生的脉冲效应的研究将是进一步要做的工作.
[1]陈兰荪.数学生态学模型及研究方法[M].北京:科学出版社,1988.
[2]Jiang Guirong,Lu Qishao,Luo Guilie.Im pulsive control of a stage-structured pestm anagem ent system[J]. Journal of Mathem atical Study,2003,36(4):331-344.
[3]桂占吉.生物动力学模型与计算机仿真[M].北京:科学出版社,2005.
[4]李万同,霍海峰.脉冲非线性生物动力系统的周期解与稳定性[D].兰州:兰州大学,2006.
[5]郑宝东,梁丽洁,张春蕊.扩展Jury判据[J].中国数学,2009,39(10):1239-1260.
[6]任庆军,窦霁虹.具有非单调功能反应和脉冲扰动的捕食系统的分析[J].纯粹数学与应用数学,2006,24(4):444-445.
[7]Cheng Huidong.Stage structured p redator-p rey m odel with im pulsive perturbations on beneficial insect and delay[J].Acta.Scientiarum Naturalium Universitatis Sunyatseni,2011,50(1):23-30.
A nalysis of stability of commensalism s Lotka-Volterra model with impulsive effect
Shi Jinxi1,Dou Jihong1,Shao Caihong2
(1.Departm ent of Mathem atics,Northwest University,X i′an 710127,China; 2.Tongliao No.1 Midd le School,Tongliao 028000,China)
Through the relationship with commensal pest population study,im pulsive differential system with the relation of comm ensalism s was establish.U ltim ate Boundedness of and the stability of equilibrium s was discussed by stroboscopic m apping and Jury criterion.Combined with theoretical analysis,proposals for pest controlwere given.
comm ensalism sm odel,im pu lsive,stroboscopic m apping,Jury criterion,stability
O175.12
A
1008-5513(2012)03-0357-06
2012-03-05.
陕西省教育厅自然科学专项基金(11JK 0511).
石金喜(1987-),硕士生,研究方向:数学建模及应用.
2010 MSC:34D 05
