推广的()展开法与Zhiber-Shabat方程的精确解

陈晓艳,吉飞宇,鱼翔

(西北大学数学系,陕西西安 710127)

陈晓艳,吉飞宇,鱼翔

(西北大学数学系,陕西西安 710127)

利用推广的()展开法,研究了Zhiber-Shabat方程的行波解,获得了其各种孤子解和周期波解,并且给出了由它得来的著名方程Liouville方程的精确解,丰富了解的范围.

推广的()展开法；Zhiber-Shabat方程；Liouville方程；周期波解

1 引言

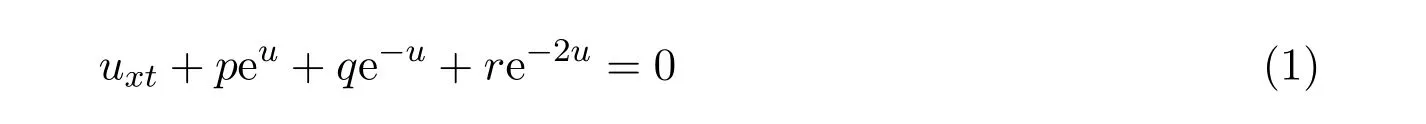
非线性演化方程Zhiber-Shabat方程在许多科学领域中有着重要的应用.由它演化得来的一些著名方程包括:当q=r=0时,方程(1)化为著名的Liouville方程；当q/=0,r=0时,方程(1)成为著名的Sinh-Gordon方程；当q=0,r/=0时,方程(1)变为著名的Dodd-Bullough-Mikhailov方程.这些方程在固体物理学,流体力学,生物数学和等离子物理学等学科中出现[12],例如Liouville方程是描述由系统的定态所构成的混合态随时间演化的规律,包括光线量子和相对论费密子等[34].Sinh-Gordon方程是在正常曲率曲面的研究中引出的,若知道它的一个非平凡解,就可以得出R2,1中类时的正常曲率曲面[5].因此这些方程得到了充分研究及应用.

到目前为止,已有很多种方法用来求解Zhiber-Shabat方程.1992年,文献[6]通过使方程(1)满足投影Riccati方程组求出方程(1)的两种精确解,后来,文献[7]用tanh函数法与推广的tanh函数法得到了方程(1)的多种行波解,文献[8-10]又分别用指数函数法,sinh-cosh函数法,F展开法对方程(1)的解的情况进行了研究.最近由文献[11]首次提出的()展开法,在研究非线性演化方程的孤子解方面,是一种方便快捷的方法,已用于求解了很多方程.

2 推广的()展开法

步骤一:对于含有两个独立变量x,t的非线性演化方程:

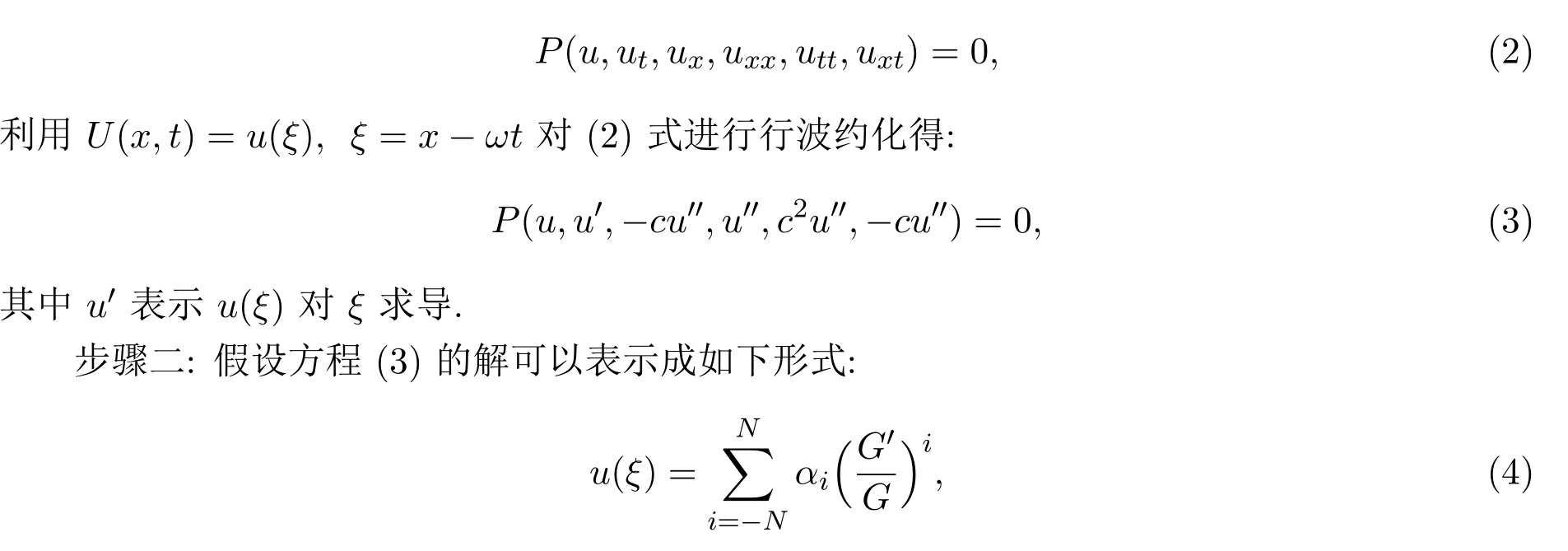
其中αi是待定系数,N是由平衡(3)式中最高阶导数项和非线性项得来的,G=G(ξ)满足二阶线性常微分方程:

步骤四:将得到的αi的值代入(4)式,利用(5)式的通解,经过分析即可以得到(2)式的精确解.

3 Zhiber-Shabat方程的行波解

令u(x,t)=u(ξ),ξ=x-ωt,ω为波速,将其代入(1)式,对(1)式进行行波约化得:

类似地,利用以上步骤还可得到著名方程Dodd-Bullough-Mikhailov方程和Sinh-Gordon方程的精确解[15].)

参考文献

[1]Fu Z,Liu S,Liu Shida.Exact solutions to double and triple sinh-Gordon equations[J].Z Naturforsch, 2004,59:933-937.

[2]Perring J k,Skyrme T H.A model unified field equation[J].Nucl.Phys.,1962,31:550-555.

[3]薛国良.光线的量子Liouville方程[J].自然杂志,1991,15(6):472-473.

[4]王仁川,朱栋培,黄卓然,等.相对论带电费密子Liouville方程[J].物理学报,1991,40(1):14-23.

[5]谷超豪,胡和生,周子翔.孤粒子理论中的达布变换及其几何应用[M].上海:上海科学技术出版社,1999.

[6]Conte R,Musette M.Link between solitary waves and projective Riccati equations[J].Phys.A,1992,25:5609-5623.

[7]Wazwaz A M.The tanh method for travelling wave solutions to the Zhiber-Shabat equation and other related equations[J].Communications in Nonlinear Science and Numerical Simulation,2008,13:584-592.

[8]张金华,丁玉敏.F展开法结合指数函数法求解Zhiber-Shabat方程的精确解[J].纯粹数学与应用数学, 2011,27(2):163-169.

[9]潘洪伟.Zhiber-Shabat方程的新的显示精确解[J].聊城大学学报:自然科学版,2010,23(3):25-27.

[10]赵云梅,芮伟国.Zhiber-Shabat方程的孤立波解与周期波解[J].纯粹数学与应用数学,2008,24(2):283-288.

[14]Borhanifar*A,Ali Zamiri Moghnlu.Application of the)-epansion method for the Zhiber-Shabat equation and other related equations[J].Mathematical and Computer Modelling,2011,54:2109-2116.

[15]Chen A Y,Huang W T,Li J B.Qualitative behavior and exact travelling wave solutions of the Zhiber-Shabat equation[J].Journal of Computational and Applied Mathematics,2009,230:559-569.A(bs)tract:The exact traveling wave solutions of the Zhiber-Shabat equation are studied by using the extended-expansion method.Solitons and periodic solutions for it are formally derived,and then the exact traveling wave solutions of the related equations,such as Liouville equation also derived,which has enriched solutions of them.

Chen Xiaoyan,Ji Feiyu,Yu Xiang
(Department of Mathematics,Northwest University,Xi′an710127,China)

extended()-expansion method,Zhiber-Shabat equation,Liouville equation, periodic wave solutions

O175

A

1008-5513(2012)04-0546-07

2011-12-22.

国家自然科学基金(10671156).

陈晓艳(1987-),硕士生,研究方向：非线性偏微分方程.

2010 MSC:35Q58,37K50