关于亚纯函数φ(z)fn(z)f(k)(z)的值分布

金瑾

(毕节学院数学与计算机科学学院,贵州 毕节 551700)

关于亚纯函数φ(z)fn(z)f(k)(z)的值分布

金瑾

(毕节学院数学与计算机科学学院,贵州 毕节 551700)

设n和k为任意的正整数,f(z)是复平面上超越亚纯函数,φ(z)为f(z)的不恒为零的小函数,讨论了亚纯函数φ(z)fn(z)f(k)(z)值分布,并提出一个新的定理,进行了较为详细的证明.

超越亚纯函数;Nevanlinna理论;值分布

1 引言与主要结果

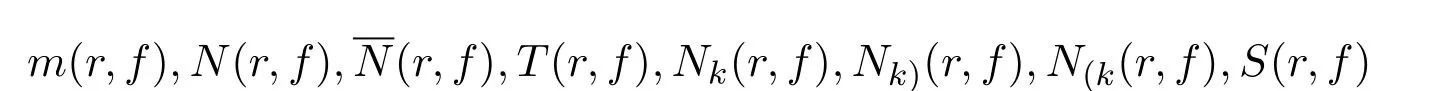
等.1959年,文献[1]证明了下面的著名定理.

定理1.1[1]设f(z)为超越亚纯函数,n为正整数,如果n≥3,则fn(z)f′(z)取每一个非零有穷复数无穷多次.

文献 [2]中还猜测:定理1.1的结论对 n=1和 n=2也成立.1979年,文献 [3]解决了n=2的情形.1995年,文献[4-5]独立地解决了n=1的情形,并得到如下定理.

定理 1.2[4-5]设f(z)为超越亚纯函数,则f(z)f′(z)取每一个非零有穷复数无穷多次.

文献[6-11]做了大量的工作并得到了许多漂亮的结果.1999年,文献[9]得到如下结果.

定理 1.3[9]设f(z)为超越整函数,n和k为正整数,f(z)的所有零点的重数至少为k,则fn(z)f(k)(z)取每一个非零有穷复数无穷多次.

文献[15]对函数f(k)(z)−afn(z)进行了研究,并得到了如下结论.

定理 1.4[15]设f(z)为平面内的超越亚纯函数,a为非零有穷复数,则当n≥k+3时,函数f(k)(z)−afn(z)有无穷多个零点.

文献[16]中证明了定理1.5和定理1.6.

定理 1.5[16]设f(z)为超越亚纯函数,k正整数,k≥2,f(z)的所有零点的重数至少为n,则对每一个 k(k≥2),f(z)f(k)(z)取每一个非零有穷复数无穷多次.其中,当 2≤k≤4时, n=k+1;当k=5时,n=5;当k≥6时,n=6.

假定读者熟悉Nevanlinna关于亚纯函数理论的标准记号和主要结果[1-31],如

定理 1.6[16]设 f(z)为超越亚纯函数,f(z)的所有零点的重数至少为 n,则f(z)f(k)(z)取每一个非零有穷复数无穷多次.至多除去三个可能的例外正整数(n=2,3,4).

文献[17]得到如下结论.

定理 1.7[17]设f(z)为平面内的超越亚纯函数,a为任意非零复数,对任意的正整数

则当m≥λ+∆+2时,

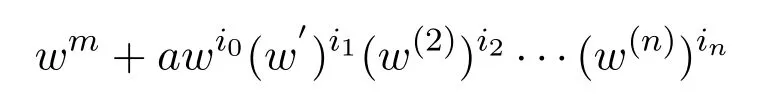
可取无穷多个零点.

文献[18]研究了f(z)+a(f′(z))n的值分布,得到下面结论.

定理 1.8[18]设f(z)为平面内的超越亚纯函数,a为非零复数,对任意的正整数n≥2,函数f(z)+a(f′(z))n取每一个有穷复数无穷多次.

在本文中,利用亚纯函数的Nevanlinna值分布理论和技巧,进一步探讨亚纯函数的值分布,得到如下结论.

定理 1.9 设n和k都是正整数,f(z)为复平面上的超越亚纯函数,φ(z)为f(z)的不恒为零的小函数,若k≤4时,

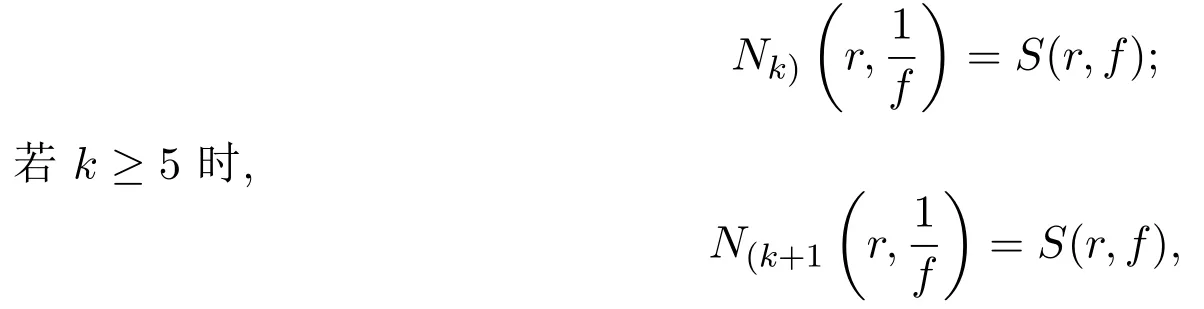
则φfnf(k)取每一个非零有穷复数无穷多次.

2 引理及其证明

引理 2.1 设f(z)为复平面上的超越亚纯函数,φ(z)为f(z)不恒为零的小函数,则

3 定理1.9的证明

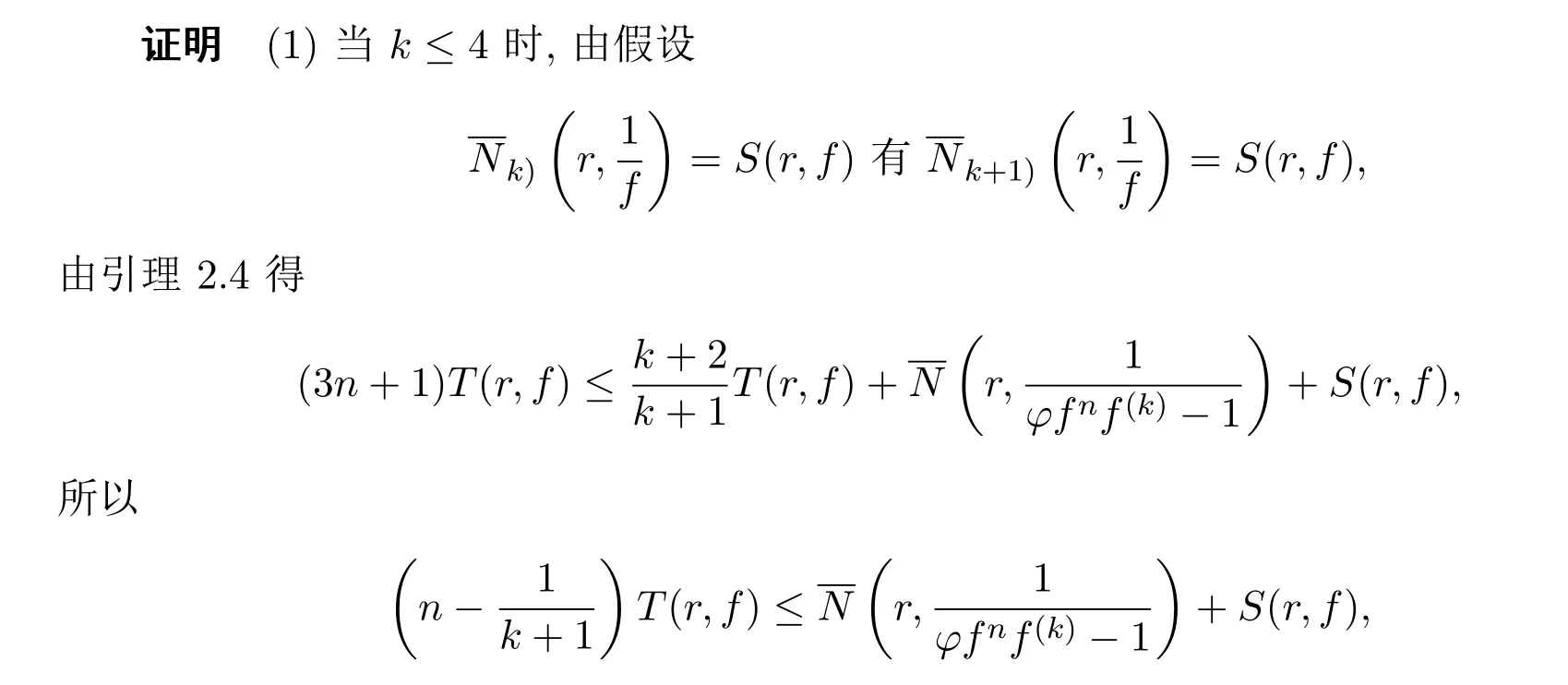
[1]Hayman W K.Picard value ofmeromorphic function and their derivatives[J].Ann.Math.,1959,70:9-42.

[2]Haym an W K.Research Problem s in Function Theory[M].London:A th lone Press,1967.

[3]M ues E.¨Uber ein p roblem von Haym an[J].M ath.Z.,1979,164:239-259.

[4]Bergweiler W,Erem enko A.On the singularities of the inverse to am erom orphic function of finite order[J]. Rev.M at.Iberoamericana,1995,11:355-373.

[5]陈怀惠,方明亮.关于fnf′值分布[J].中国科学,1995,25(2):121-127.

[6]Sons L R.Deficiencies ofm onom iais[J].M ath.Z.,1969,111:53-68.

[7]Steinmetz N.¨Uber die nullstellen von diff erential polynomen[J].Math.Z.,1981,176:255-264.

[8]刘瑞,高凌云.一类复微分方程的亚纯允许解的值分布[J].纯粹数学与应用数学,2012,28(1):25-28.

[9]Pang X C,Zalcmam L.On theorem s of Hayman and clunie[J].New Zealand J.Math.,1999,28:71-75.

[10]Wang J P.On the zeros of fnf(k)−c[J].Com p lex Variables,2003,48(8):695-703.

[11]王建平.关于f(k)f−a的零点之猜测[J].数学进展,2002,31(1):41-46.

[12]Haym an W K.M erom orphic Functions[M].Ox ford:Clarendon Press,1964.

[13]Yi Hongxun,Yang Chungchun.Uniqueness Theory of M erom orphic Functions[M].K luwer:Science Press, 2003.

[14]Doeringer W.Exceptional values of diff eretial polynom ials[J].Pacific J.of M ath.,1982,98:55-62.

[15]张站亮.关于f(k)(z)−afn(z)的零点[J].数学实践与认识,2004,31(11):129-134.

[16]王建平,仪洪勋.亚纯函数理论的一个基本不等式及其应用[J].数学学报,2006,49(2):443-450.

[17]江秀海,高凌云.关于wm+awio(w′)i1···(w(n))in的值分布[J].纯粹数学与应用数学,2007,23(1):17-20.

[18]方明亮,Law rence Zalcm an.关于f(z)+a(f′(z))n的值分布[J].中国科学,2008,38(3):279-285.

[19]Clunie J.On integral and meromorphic function[J].J.London Math.Soc.,1962,98:55-62.

[20]何育赞,萧修治.代数体函数与常微分方程[M].北京:科学出版社,1988．

[21]Golubew W W.Vorlesungen¨Uber Diff erential G leichungen im Kom p lexen[M].Berlin:Duetscher Verlag der W issenschaften,1958.

[22]刘慧芳.一类亚纯系数微分方程解的增长性[J].纯粹数学与应用数学,2008,24(1):25-29.

[23]陈玉.某类线性微分方程亚纯解的增长性[J].纯粹数学与应用数学,2009,25(2):261-267.

[24]金瑾.复方程f′′+Af=0的解的零点充满圆[J].数学进展,2005,34(5):609-613.

[25]金瑾.高阶微分方程的解及其解的导数的不动点[J].数学研究与评论,2007,27(4):803-813.

[26]金瑾.高阶线性微分方程解的二阶导数的不动点[J].数学理论与实践,2007,27(4):107-113.

[27]金瑾.一类高阶齐次线性微分方程亚纯解的超级及其不动点[J].华中师范大学学报:自然科学版,2011,45(1):18-22.

[28]Jin Jin.The hyper order of solutions of higher order linear diff erential equations with analytic coeffi cients in the unit disc[C]//Proceedings of the 5th International Congress on M athem atical Biology.Qingdao: Qingdao Agriculture,2011.

[29]Jin Jin.The fix point and hyper of solutions of higher order hom ogeneous linear diff erential equations with m erom orphic function coeffi cents[C]//Proceedings of the 5th International Congress on M athem atical Biology.Qingdao:Qingdao Agriculture,2011.

[30]金瑾,石宁生.一类微分方程的解及其解的导数与不动点的关系[J].数学实践与认识,2011,41(22):185-190.

[31]仪洪勋,杨重骏.亚纯函数唯一性理论[M].北京:科学出版社,1995.

The valued istribu tion of the m erom orphic function φ(z)fn(z)f(k)(z)

Jin Jin

(Departm ent of M athem atics and Com puter Science,Bijie University,Bijie 551700,China)

Let n and k be positive integer,f(z)be a transcendentalm erom orphic function in the com p lex p lane, andφ(z)be small function of not constant zero of f(z).Value distributions of atranscendentalmeromorphic functionφ(z)fn(z)f(k)(z)is discussed in this paper,and a new theorem is presented and proved in m ore details.

transcendentalm erom orphic function,Nevanlinna theory,value distribution

O174.52

A

1008-5513(2012)06-0711-08

2012-02-10.

贵州省科学技术基金(2012GZ10526);贵州省毕节地区科研基金([2011]02).

金瑾(1962-),教授,研究方向:复分析.

2010 M SC:30D35