电力物资应急配送体系最优路径模型设计
2012-07-05张国英张宏伟华北电力物资总公司北京100075
张国英,张宏伟, 郅 青 (华北电力物资总公司,北京 100075)
电力作为当今人们生活和工作必不可少的能源,它的中断会给用户和社会造成巨大的影响,尤其是近年来,雪灾、地震等自然灾害频发,电网的安全生产面临着更加严峻的考验,其抢险救灾对应急物资的需求要求越来越高,因此,构建高效科学的电力物资应急配送体系具有重要的意义。
本文引入管理学中应急物流管理的理念,结合电网运行及应急物资需求的特点着力解决电力物资应急配送体系中的最优路径问题,通过对称三角模糊数表示物资运输期间的不确定性因素,建立模糊运输网络模型,搜索物资配送的最高保障率路径。
1 应急配送体系最优路径模型
本文中将电网各个物资仓库和被破坏的输电线路抽象为节点,而节点之间的连线距离代表两节点间物资运送的时间。
由于电力系统物资需求的季节性和复杂性,根据具体的运输条件只能对运输时间做出一个近似的模糊估计,此外其社会公益性要求在发生事故后抢险物资的到达也有时间限制。本文引入对称三角模糊数来表示这种时间的不确定性,引入保障率指标来寻找最优路径,在上述条件下建立电力抢险物资调配最优路径的数学模型。
设S1,S2,…,Sn为当前的n个电力物资储备仓库,D1,D2,…,Dm为m条被破坏的输电线路即电力物资需求点,它们分布在图G V,()E 的节点上,物资储备仓库与物资需求点之间通过交通道路相连。图G中除上述节点外的其余节点代表交通枢纽。对G中的每一条边e对应权值为ω()e,在模型中代表物资在两个节点之间的运送时间。
设Rij为Si到Dj的所有通路的集合,若P是G中连接任意两点的一条路,路P的权为P中所有边的权之和记为ω()P :


在上述模型中,ω()P 为对称三角模糊数,因此路径之间通常无法直接比较,本文通过引入保障率指标来解决这一问题。
定义保障率M P,()t为路径P的运输时间小于等于限制期t的程度。对保障率进行有效而准确的分析,可以衡量路径承担运输风险的能力。对任意一个对称三角模糊数:

对时间限制t得出路径P的保障率指标表达式如下:
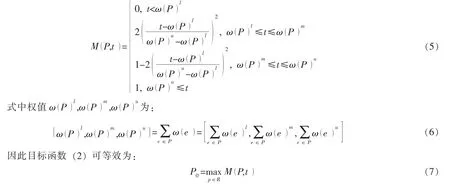
2 模型的求解
因路径权值由三角模糊数表示,不能直接运用最短路算法,式 (7)可转化为如下等价形式求解。


式中x0∈-1,[]0 ,P0对应保障率:由于式 (8)是一个较复杂的非线性路径问题,进一步将这一问题进行转化。

P(x)为给定值时,式 (10)的最优解对应的路径,因此问题最终转化为先求x的值,再利用最短路算法,求取最优路径。

x的求解步骤如下:
①令x=0, 若Q(0 )≤t, 则P(0 )为最优路径, 否则进入②;
②令x=-1,若Q(-1)>t,则P(-1 )为最优路径, 否则进入③;
设tj为物资需求点Dj的物资运送限制期,Pij表示从Si到Di的最高保障率路,其保障率用M tij,tj()表示,均可通过上述模型求解。通过求解,可以分别得出每一个物资仓库到每一个物资需求点的最高保障率路径,并计算出通过该路径运输物资的时间范围。根据式(5)计算出路径对应保障率指标M tij,tj(),反映出通过此路径能按时运达物资的风险大小,为应急电力物资调配方案的确立奠定基础。
3 最优路径的算例分析
如图1所示,该网络为一边权为对称三角模糊的模糊交通网络。
以IEEE 14节点系统为例,假设事故时线路6-13、2-5、6-11、12-13、5-4退出运行,对相应受损设备进行抢修需电力物资的供给才能进行,分别将以上线路和物资仓库抽象为交通网络图中的节点。线路与节点对应关系如表1。物资仓库与节点对应关系如表2。

表1 线路节点对应关系表

表2 仓库节点对应关系表
假设事故后所有物资需求点要求物资在24h内运达才能满足电力抢险应急要求,用本文的方法搜索从物资仓库到需求点的最优路径及对应保障率 (部分结果)如表3所示。

表3 最优路径及对应保障率

图1 模糊配送网络
4 结束语
针对应急情况下电力物资的综合调配问题,本文建立了多物资供应点、多物资需求点的物资应急配送体系模型,通过引入对称三角模糊数描述现实世界的不确定性因素并通过保障率指标对模糊目标进行转化求解。本文提出的评估线路重要性指标只能在一定程度上反映输电线路恢复对电网的影响,事实上影响调配方案的因素除了时间,还受成本等其他因素影响,如何在更复杂情况下建立多目标的电力物资应急配送体系是今后的研究方向。
