基于鲁棒优化算法的小型无人机模糊控制器研究

孙大伟， 许国栋

(中国空空导弹研究院，河南 洛阳 471009)

0 引言

模糊控制器的应用是现代控制理论中一个比较重要的研究方向，特别是在飞行控制课题中，当飞行器发生飞控传感器失灵、性能参数指示不精确、外界紊流的干扰等特殊情况时，利用模糊控制技术来提高整体系统的适应性和可靠性，已成为提高飞行器安全性能的一种十分有效的解决手段。欧美［1-4］和俄罗斯［5］科学家在飞行控制系统内结合模糊控制技术的研究上都取得了长足的进步，一些研究成果已在小型无人飞行器(SUAV)上得到应用。

1 鲁棒H2/H∞优化算法简介

从文献［2-3］可知，模糊控制器的构造一般都参照经典(Crisp)控制器的结构原理，其中包括微分和积分动态反馈，以及为经典控制器求取的增益系数，都可以被转换到模糊控制系统中。典型的控制系统最优系数求解方法如文献［6］，其离散模型的标准形式如图1所示。

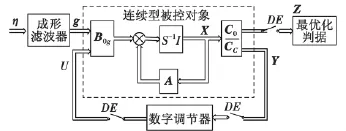
图1 无人机离散模型Fig.1 Discrete model of SUAV

外部扰动向量g(涡流速度随机向量)为Dryden模型［7］，为了通用化将此模型转化成了多维成形滤波器形式，其输入由白噪声η激发。成形滤波器的状态空间为四子集矩阵［Af，Bf，Cf，Df］只有在随机扰动时被启用。矩阵B0g将控制输入u和扰动输入g结合为一个控制输入向量A为SUAV的状态空间矩阵，C0为输出向量Z的观测矩阵，而Z被用来计算系统控制品质，而Cc为真实闭环系统输出Y的观测矩阵。成形滤波器DE为离散开关，周期为Ts，连续型被控对象的闭环系统为四子集矩阵［A，B0g，Cc，Dc］，另一个四子集矩阵［A，B0g，C0，D0］被用来做最优化判断。SUAV 纵向运动的状态向量 X=［v，α，q，ϑ，h］T，包括真空速、攻角、俯仰角速度、俯仰角和高度。观测两类SUAV应用模型:标称模型(无扰空速vnom)和参数扰动模型(受扰空速vpert)，为了计算这两类模型的控制品质和鲁棒性，采用了H2/H∞鲁棒优化算法。

定常扰动下离散系统每个模型(标称和参数扰动)的H2范数为

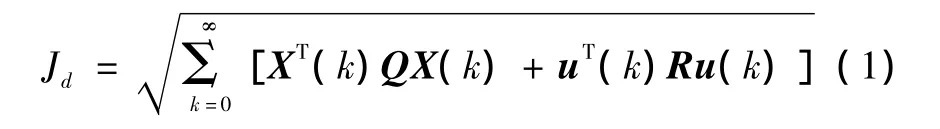
随机扰动下每个模型的H2范数为

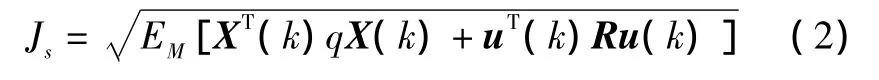
每个模型的H∞范数为

式中，wN为奈克维斯达频率，wN=π/Ts。

式(1)，式(2)中:X为状态空间变量;u为控制向量;EM为数学期望算子;Q和R为权矩阵。式(3)中，为敏感度函数矩阵T(jw)在频域0≤w≤wN内的最大奇异值［8］，用来计算系统鲁棒性。相对于图1，矩阵T为:T(z)=K(z)G(z)［E+K(z)G(z)］-1。式中:z=exp(jwTs);G(z)和K(z)为SUAV执行机构和调节器的传递函数矩阵。

可以得到Pp-r(控制品质-鲁棒性)H2/H∞优化判据为

λd，，λs和 λ∞，为相应的权系数，它们被用来平衡定常和随机扰动情况下系统控制品质和鲁棒性之间的关系，式(4)反映了控制器Cn(n为优化判据的步长范数)可变参数的向量函数，此向量囊括控制器的可调节参数，执行优化的结果为

Dc为控制器参数在空间中的稳定区域。SUAV纵向运动标称模型(vnom=250 km/h)和参数扰动模型(vpert=200 km/h)的状态矩阵和控制矩阵为

下标“p”表示参数扰动。本SUAV的纵向运动只受控于升降舵:u=δe。经典控制器的结构如图2所示。由俯仰角和俯仰角速度传感器以及相应增益系数Ks和Kq组成的角度稳定通道，可以自动求出俯仰角的稳态值，而高度稳定器Wh(z)由预置输入稳定高度。角稳定器Wα(z)和高度稳定器都是简单的数字PD控制器。

图2 自动驾驶仪结构图Fig.2 Autopilot of SUAV

2 模糊飞行控制器

根据文献［2］的建议可知，为了减少飞控计算机能耗并提高系统鲁棒性，可以在原型机的基础上用模糊控制器替换上述的控制器，其结构如图3所示。

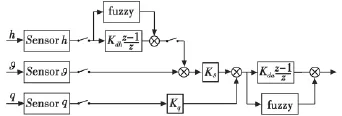
图3 模糊飞行控制器结构图Fig.3 Fuzzy autopilot of SUAV

图中，fuzzy表示模糊控制器模块，为双输入单输出模糊控制器。模糊控制器的结构如图4所示，采用三角隶属度函数，相应的表达式为

式中:i为隶属函数序号;a，b，c为函数顶点。而输入信号模糊度值为

图4 模糊控制器Fig.4 Fuzzy controller

知识库的模糊规则根据原型控制器的数据进行规划，并进行适当的调整。总共启用25条规则，初始的模糊规则库如表1所示。

表1 初始俯仰角通道模糊规则库Table 1 Initial fuzzy logic base for pitch

为了使规则库的控制面尽量贴合实际，在原型机控制经验参数的基础上，对初始模糊规则库进行了重新规划，规划结果如表2。

表2 处理后俯仰角通道模糊规则库Table 2 Optimized fuzzy logic base for pitch

模糊控制器的解模糊采用重心法，表达式为

3 原型机、模糊控制器动态特性比较

在SIMULINK中，将原型控制器与模糊控制器在定常和随机扰动情况下，分别对SUAV纵向运动控制系统的标称和参数扰动模型进行仿真分析比较，这里取了几个主要参数，如图5～图10和表3～表4所示。

图5 标称模型高度比较图Fig.5 Comparison of nominal model in height

图6 标称模型俯仰角比较图Fig.6 Comparison of nominal model in pitch

图7 标称模型俯仰角速度比较图Fig.7 Comparison of nominal model in pitch angular velocity

图8 参数扰动模型高度比较图Fig.8 Comparison of perturbed model in height

图9 参数扰动模型俯仰角比较图Fig.9 Comparison of perturbed model in pitch

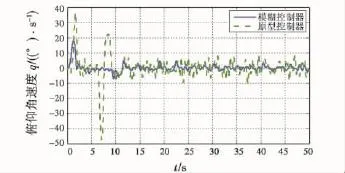
图10 参数扰动模型俯仰角速度比较图Fig.10 Comparison of perturbed model in pitch angular velocity

表3 定常信号下标称和扰动系统的性能指标Table 3 Comparison of the fuzzy and crisp systems'step responses

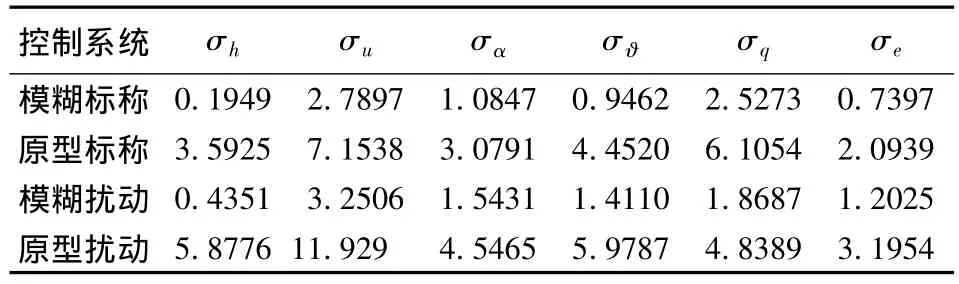
表4 随机信号下标称和扰动系统的协方差Table 4 Comparison of the state variables'RMS of the fuzzy and crisp systems

4 结论

比较原型控制器和模糊数字控制器，发现在保持同一级别鲁棒性的情况下，模糊控制器拥有更好的飞控品质;在定常信号下，无论是标称模型还是参数扰动模型，模糊控制器都拥有更小的调整时间和相位差;在随机信号下，模糊控制器能更有效地压制外部扰动，并且所有的协方差也小一些;模糊控制器完全能满足NPRS［9］(Nominal Performance Robust Stability)方法的要求。虽然模糊控制器的鲁棒性更胜一筹，但是其模糊规则库的优化是个难题，在后续工作中将对此开展研究。

［1］SCHRAM,G,KAYMAK U,VERBRUGGEN,H B.Fuzzy logic control［M］.New York:Berlin Springer-Verlag,1993.

［2］SCRAM G,VERBRUGGEN H B.A fuzzy control approach［M］.New York:Berlin Springcr-Verlg，1991.

［3］LIN C F.Advanced control systems design［M］.New Jersey:PTR Prentice Hall Inc,Englewood Cliffs,1994.

［4］DRIANKOV D,HELLENDOORN H,REINFRANK M.An introduction to fuzzy control［M］.New York:Berlin Springcr-Verlg，1991.

［5］УЛЬЯНОВ С В.Нечеткие модели интеллектуальных систем управления:теоретические и прикладные аспекты (обзор)［J］.Изве.АН СССР.Сер.Техническая кибернетика.1991(3):3-29.

［6］TUNIK A A,ABRAMOVICH E A.Parametric robust optimization of the digital flight control systems［J］.Proceedings of the National Aviation University.2003,17(2):31-38.

［7］MCLEAN D.Automatic flight control systems［M］.Prentice Hall Inc.,Englewood Cliffs,1990.

［8］KWAKERNAAK,H.Robust control and H∞-optimization［J］.Tutorial paper.Automatica.1993,29(2):255-273.

［9］UNIK A A,RYU H,LEE H C.Parametric optimiz-ation procedure for robust flight control system design［J］.KSAS International Journal Seoul.2001，2(2):95-107.