多雷达距离测量空间定位方法及精度分析

常 清， 潘江怀， 安 瑾

(江苏自动化研究所，江苏 连云港 222006)

0 引言

多平台雷达组网需要综合利用各平台的雷达信息，获得对目标位置一致、精确的定位，形成统一的态势。在信息融合过程中，为了对各雷达信息进行综合处理，需要将各平台雷达探测信息转换到公共参考坐标系(即相同的时空参考坐标系)中。理想情况下，同一时刻各雷达探测结果应重合。但由于雷达测量误差尤其是系统误差的存在，使得各雷达探测结果之间存在较大差异，影响量测(局部航迹)和航迹的关联、目标跟踪及航迹状态估计，造成目标冗余、航迹精度降低、航迹零碎等情况的出现，影响战场态势一致性。通常，雷达的测距可以利用对固定目标的探测进行静态标定，以减少其测距的系统误差，而且可以较好地保持;而雷达的测向(尤其是动平台雷达，如舰载/机载雷达)，其系统误差受到雷达测量误差、甲板形变误差、平台定位误差、平台姿态误差、时间误差等综合影响，一般较难通过简单的标校进行校正，且校正后一般很难保持。因此在一般情况下，雷达的测距精度比较高，而测向精度较低，在有多部雷达组网时，可以利用多部雷达对同一目标的距离交汇对目标进行定位。

1 多雷达距离测量空间定位模型

基于ECEF的三雷达距离测量空间定位示意图如图1所示。

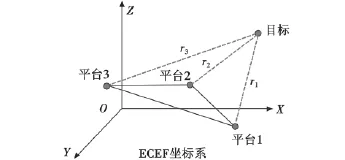
图1 三雷达距离测量空间定位示意图Fig.1 Range detecting space location of the three radars

三部雷达所在的位置为(Li，Bi，Hi)，i=1，2，3，各雷达对目标的测距为 r1，r2，r3。

由ECEF坐标转换可知，各平台在ECEF坐标系中的位置为(xpi，ypi，zpi)，i=1，2，3，假设目标在 ECEF坐标中的位置为x，y，z，则由空间定位可知

由平台站址坐标，可以计算出雷达站之间基线长度为

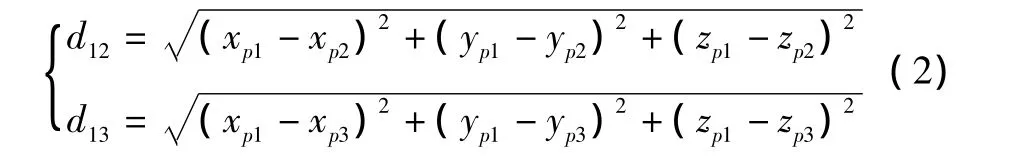
基线的方向余弦为

两基线之间的夹角为

r1在基线d12和 d13上的投影分别为

则目标在ECEF坐标系中位置为

2 多雷达距离测量空间定位精度分析

根据各平台雷达给出的测距信息，可直接由各雷达测距精度解算出目标的位置精度。测距误差方程为

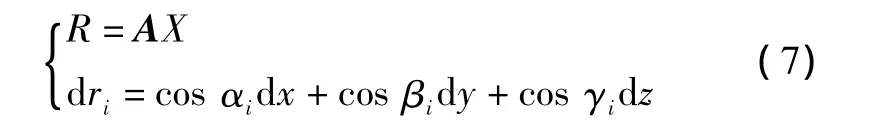
式中，cos αi，cos βi，cos γi为平台到目标的方向余弦。矩阵形式表示为

下面分等精度和不等精度情况。

1)等精度测距。

当各平台雷达测距精度相近时(假设测距精度为μ2)，则目标点位置误差为

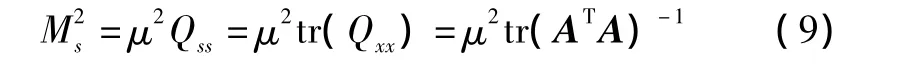
根据矩阵迹的性质可知:tr(AB)=tr(BA)-1

则有

式中，φ12，φ13，φ23为测距三雷达测距 r1，r2，r3之间的空间夹角;N为矩阵的行列式值。

所以

该式表明，目标S的精度除受测距精度的影响外，完全取决于测距交汇的空间图形，而空间图形以各测距之间的交汇角表示。所以，一旦知道距离的测量值，便可立即估计，不需要目标的近似坐标，对误差的分析计算更加直接，对各平台的优化布局具有指导意义。

2)不等精度测距。

当各平台雷达测距精度相差较大时，对各平台测距设定一个加权系数 Pi=μ2/，μ为单位权标准偏差，为各平台测距精度，则目标点位置误差为

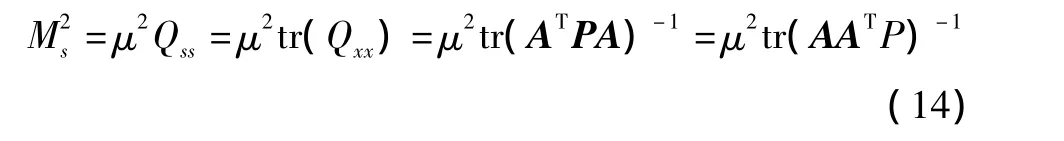
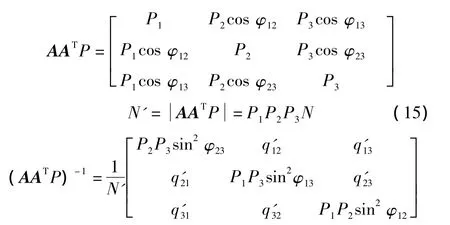
故可得误差计算式为

3 空间最优定位点计算

因为不等精度测量表达式与等精度测量表达式一致，为简化起见，在最优定位点的分析上只讨论等精度测距。等精度测距定位点误差可表示为

式中，Q=sin2φ12+sin2φ13+sin2φ23。

由优化求解可知，在上式的解为cos φ12=cos φ13=cos φ23=0，即

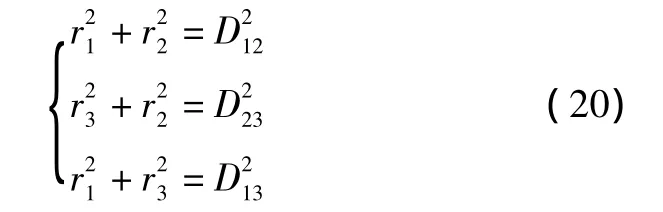
方程(20)有唯一解，说明三平台的最优定位点是唯一的。而且通过解析几何可知，利用简单的几何关系就可以计算出取得最优定位点的最优边长。通过最优边长的计算也可以粗略地估计测量精度。在测量中，应优化平台位置，使被测物体尽量位于最佳交汇点附近。

当S点为最优定位点时，平面角度有如下方程

所以0°＜cos∠213＜90°，同理，0°＜cos∠123 ＜90°，0°＜cos∠132＜90°。这样，就可以知道最优定位的第一个必要条件:当S为最优定位点时，平台组成的平面三角形必需为锐角三角形。

当S点为最优定位点时，三个平台位置组成的平面方程为

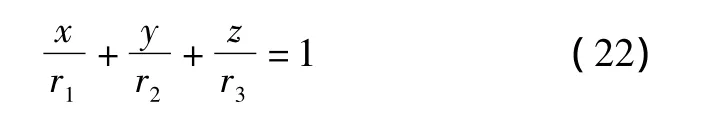
S点至平面的距离为

三条测距相对于平台平面的夹角为

即有，sin2ε1+sin2ε2+sin2ε3=1。

假设三平台构成等边三角形，待测目标S在三角形的正上方变动。则待测目标S至各平台的距离误差方程式可写成

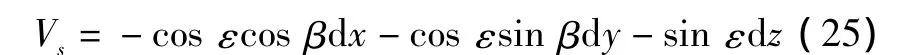
式中:ε为平台对目标的仰角;β为方位角。组成法方程并消去交叉项的方程系数矩阵为

则待测目标S的平面位置中误差及三维点位中误差为

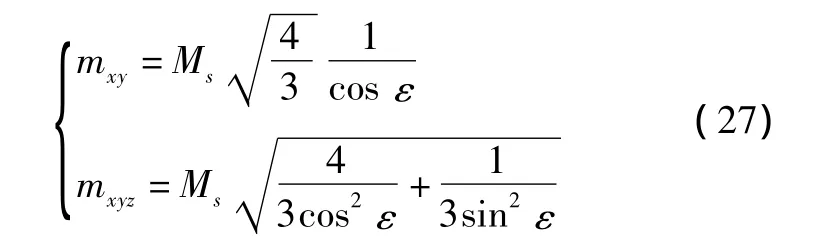
由上述分析得到如下结果。

2)雷达俯仰角ε越小，平面位置精度越高，但高程精度却大幅度降低;ε越大，平面精度越低，但高程精度却较高。

取雷达测距精度为σr=50 m时，目标定位精度随ε变化的曲线如图2所示。

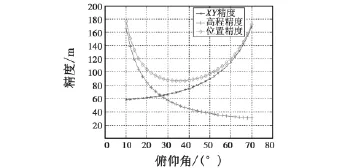
图2 目标定位精度随俯仰角变化的曲线图Fig.2 Target location precision vs elevation

4 仿真验证

设雷达1，2，3 的大地坐标分别为 (121.2°，26.5°，0 m)，(121.3°，26.5°，0 m)，(121.3°，26.4°，0 m)，探测精度为(100 m，0.3°)。目标的运动轨迹为(L(k)，26.7°，2000 m)，L(k)=120.95+(k-1)*0.008，k=1，2，…，100，仿真场景如图 3 所示，目标定位结果如图4所示。

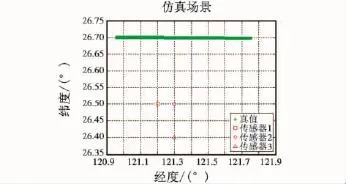
图3 仿真场景Fig.3 Scene of simulation

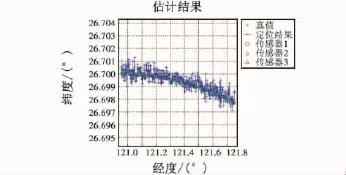
图4 定位结果局部放大图Fig.4 Locating results of partial enlargement

从仿真的效果可以看出，基于多雷达的距离量测的定位精度可以较好地实现目标定位，其最大误差在110 m左右，和雷达的测距精度相当。

5 小结

针对雷达的测距精度一般比较高，而测向精度较低的情况，本文提出了一种基于多雷达距离测量空间定位方法。该方法基于ECEF坐标系，根据雷达站之间基线长度和方向余弦，将各雷达对目标距离测量在方向余弦上进行投影，进一步计算目标在ECEF坐标系中的空间位置。此方法只需要确定各雷达站的大地坐标，就可以给出目标的大地坐标，可以有效解决地球曲率所带来的坐标转换问题，并且不涉及高次方程组和多值解判断，也不涉及迭代初值计算。该定位系统不仅能得到较高的定位精度，同时，作用距离可以很远。通过对目标定位的精度分析可知:1)目标定位精度不仅与雷达测距精度有关，还取决于平台与目标的测距交汇的空间图形，而空间图形以各测距之间的交汇角表示;2)雷达俯仰角越小，平面位置精度越高，但高程精度却大幅度降低;俯仰角越大，平面精度越低，但高程精度却较高。本研究对于多雷达的布站具有一定的指导意义。

［1］FISCHER W L,MUEHE C E.Registration errors in a netted air surveillance system［R］.Report 1980-40,MIT Lincoln Lab,Sept,1980.

［2］DANA M P.Registration:a prerequisite for multiple sensor tracking［M］.Multitarget Multisensor Tracking:Advanced Application.Artech House Inc,1990.

［3］韩崇昭，周彬，元向辉，等，共同杂波环境下多目标量测数据的误差传递与校正［J］.自动化学报，2007，33(7):771-774.

［4］NABAA N,BISHOP R H.Solution to a multisensor tracking problem with sensor registration errors［J］.IEEE Transactions on Aerospace and Electronic Systems,1999，35(1):354-363.

［5］潘江怀，李洪梅，何佳洲.三维传感器组网偏差估计方法［J］.火力与指挥控制，2008，33(4):104-106.

［6］何友，修建娟，张晶伟.雷达数据处理及应用［M］.北京:电子工业出版社，2009.

［7］潘江怀，何佳洲，罗双喜.舰载雷达探测误差传递与灵敏度分析［C］//第三届中国信息融合大会，2011:514-520.

［8］HERMAN S M,POORE A B.Nonlinear least-squares estimation for radar and navigation biases［C］//Proceedings of SPIE Signal and Data Processing of Small Targets,2006，6236:1701-1717.

［9］OKELLO N N,RISTIC B.Maximum likelihood registration for multiple dissimilar radars［J］IEEE Transactions on Aerospace and Electronic Systems,2003,39(3):1074-1083.

［10］CRUZ D，ALOUANI E J，RICE A T，et al.Radar registration in multiradar systems［M］.In Proceedings of the SPIE Symposium on Aerospace Sensing,1698,Orlando,FL,1992.