电阻式触摸屏校准算法的优化

蔡红娟，高恒强，蔡 苗

（1.华中科技大学 武昌分校 电工电子教学基地，武汉 430064；2.中国地质大学(武汉) 机电学院，武汉 430074）

0 引言

触摸屏广泛应用于工业控制领域的人机交互和控制设备，简化了用户的操作[1]，提供了更加友好直接的人机交互。市场上较为常见的触摸屏有：红外线触摸屏、电容式触摸屏、电阻式触摸屏和表面声波触摸屏。目前，市场上应用比较多的是电阻式触摸屏。然而电阻式触摸屏在出厂时由于LCD显示屏与触摸屏之间装配的不对应会引起机械误差，主要有位移误差、放大误差和旋转误差[3]，从而导致触摸屏上绘制的图形与LCD显示屏上的图形对应的集合会有所偏差，使之无法准确的产生对应点的x和y坐标。为了解决这个问题，几乎所有带阻性的触摸屏投入使用前均要经过一定的校准[9]。

由于触摸屏的密度不一致，采用简单的基本线性校准还是会存在一定的误差，为了获得更高的校准精度，在此数学推理的基础上，本文进一步提出了触摸屏校准的优化算法，并以嵌入式硬件为平台，采集触摸屏检测数据作为测试样本，对两种校准算法进行了测试比较，结果表明，优化算法可以获得更高的校准精度。

1 电阻式触摸屏的工作原理

典型的电阻式触摸屏一般由三部分构成：两层透明的阻性导电层，在两层导电层之间的隔离层以及电极[6]。电阻式触摸屏示意图如图1所示。

电阻式触摸屏就相当于一种传感器，利用压力感应进行控制，将矩形区域中触摸点(x, y)的物理位置转换为代表x坐标和y坐标的电压[5]。触摸屏工作时，上下导电层相当于电阻网络，当某一层电极加上电压时，会在该网络上形成电压梯度。如果有外力使得上下两层在某一点接触，则在电极未加电压的另一层可以检测到接触点处的电压，经过A/D转换知道接触点处的坐标[8]。比如，在Y+电极上加驱动电压VCC，Y-电极接地，则顶层导电层( Y+, Y-)上形成电压梯度，X+作为引出端测量接触点的电压，当有外力使得上下两层导电层有在某一点(x1,y1)接触，则在X+处可测得电压为VX+，由于导电层均匀导电，则可以认为触点电压与驱动电压之比即为触点Y坐标与触摸屏高度之比，即y1=(VX+/ VCC)*height。同理，将驱动电压施加在X+电极，并在Y+处测量触点电压，从而可以获得该点的x坐标。

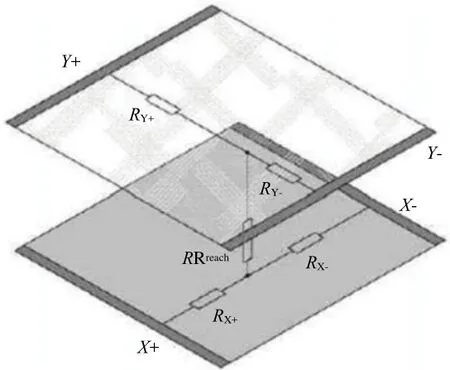
图1 电阻式触摸屏示意图

由压力感应得到坐标值的并不能达到100%的精度，它存在着误差，尤其是触摸屏本身电阻材料的均匀性以及出厂安装时存在的机械误差，直接影响到了触摸屏的精度。因此，在使用触摸屏时，需要将触摸屏上的图形经过一定的变换，换算出与LCD显示屏相一致的点集合，这种图形重建的过程就是校准。

2 触摸屏的基本线性校准算法

触摸屏和LCD显示屏叠加在配套使用时，由于存在误差，触摸屏坐标系和显示屏坐标系不重合，校准的目的就是在这两种坐标系之间找到一种合适正确的映射关系，使触摸屏上显示的图形经过变换，与LCD显示的图形保持一致[7]。这里触摸屏和LCD显示图形的点都用矢量来表示[2,4]：Q( x, y )为触摸屏上的点，称为物理坐标；Qd( xd, yd)为LCD显示屏上的点，称为显示坐标。设物理坐标：

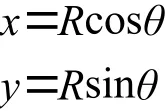
由于触摸屏和LCD显示屏接触点之间存在角度误差，同时考虑到每个点的x和y坐标都存在不同的因子缩放，并且触摸屏和LCD显示屏之间还存在移动误差，则假设角度差为φ，缩放因子为kx和ky，位移因子为Sx和Sy，可得到显示坐标：

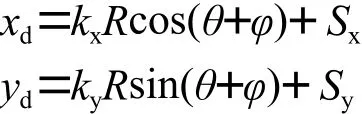
一般情况，触摸屏和LCD显示屏之间的角度误差φ极小，则sinφ≈φ，cosφ≈1。那么，LCD显示屏上点坐标可以化简为：

由上式中可以看出，除了x和y，方程式右边各项均为常量，即触摸屏和显示屏的坐标系可以认为是线性的，基于此方程实现的校准也称为线性校准。现在用一般情况来代替各乘积项的系数，则可以得到：

显然，如果能求出线性变换的参数( A1, B1, C1,A2, B2, C2)，就可以通过上述等式来校准从触摸屏那里得来的显示坐标了[5]。为了求出这六个参数，在触摸屏上任意取三个点（由于边界点的线性度差，所以要尽量避免），设物理坐标和显示坐标分别为(x1, y1)、(x2, y2)、(x3, y3)和 (xd1, yd1)、(xd2, yd2)、(xd3, yd3)，可以得到方程组：

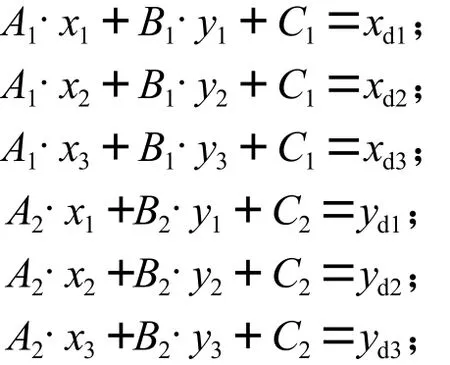
解方程组可得：

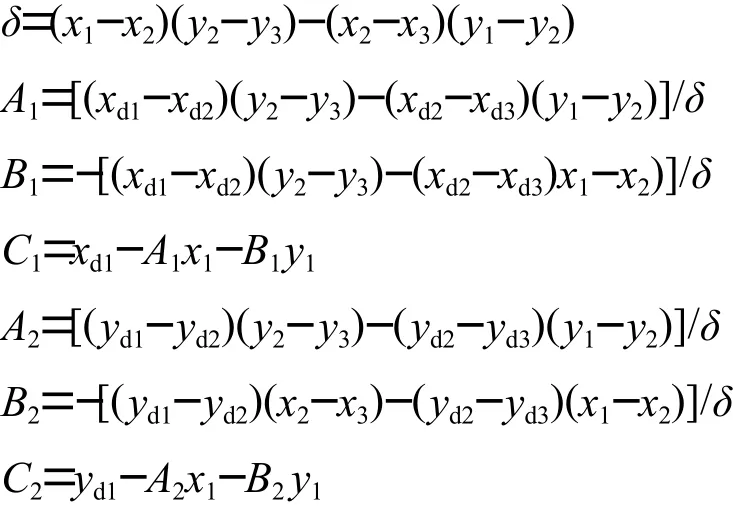
值得注意的是，只有在触摸屏和LCD显示屏之间的角度误差φ极小的情况下，上述的基本线性校准算法才适用。为了达到更好的校准效果，本文在此基础上，对基本线性校准算法进行了优化，形成五点校准。

3 校准算法的优化

为了使校准更加精确，现在触摸屏上任意取五个点，设物理坐标和显示坐标分别为(x1, y1)、(x2, y2)、(x3, y3)、(x4, y4)、(x5, y5) 和 (xd1, yd1)、(xd2, yd2)、(xd3, yd3)、(xd4, yd4)、(xd5, yd5)，代入 x 坐标方程xd=A1·x+B1·y+ C1，可以得到方程组：

对等式做如下处理：

第一步，将原方程5个等式直接相加，得第1个总等式：

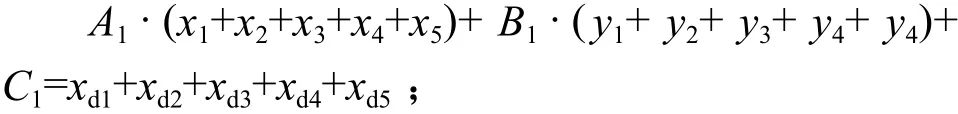
第二步，将原方程5个等式分别乘以参数x，然后5个等式相加，得第2个总等式：

第三步，将原方程5个等式分别乘以参数y，然后5个等式相加，得第3个总等式：

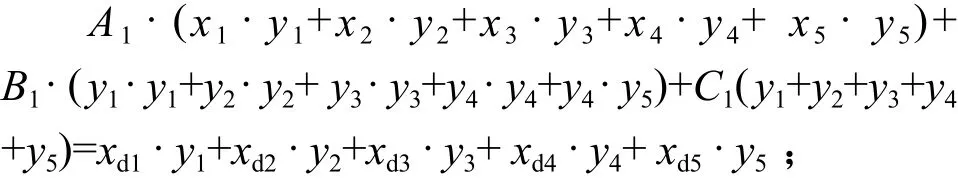
由这三个总等式构成一个x坐标的三阶线性方程组，用克莱姆法则可以将参数A1，B1，C1求出。

同理，可以得到y坐标的三阶线性方程组：

用克莱姆法则可以将参数A2，B2，C2求出。

4 校准测试与比较

这里采用的触摸屏校准的测试环境是：基于s3c2410的ARM9开发板，外界五线电阻式触摸屏和640×480像素16灰度级液晶屏，使用μcos-Ⅱ操作系统，开发板与PC机通过串口连接。

在触摸屏的(73,154)、(891,516)、(512,939)三点位置均显示“+”，用笔依次点击三个点，获得这三个点的显示坐标分别为(30,30)、(210,120)、(120,210)，带入基本线性校准算法的方程组，可计算校准系数如下：A1=108720，B1=-5400，C1=7391400，A2=5490，B2=107730，C2=-2494830。

然后在触摸屏 (265,414)、(606,171)、(768,700)、(111,956)、(448,580)五个点的位置均显示“+”，并依次点击，通过上述的校准系数对触摸屏进行校准，得到结果如图2所示。

图2 基本线性校准法校准测试

图中，“Screen Sample”是触摸屏坐标，“Translated Sample”是通过校准之后的得到的显示坐标，“Display Sample”是采样时直接获得的显示坐标。由图右边两列坐标可知，通过基本线性校准之后，计算值“Translated Sample”与理论值“Display Sample”比较接近，达到了校准目的，但还是存在着一定误差。

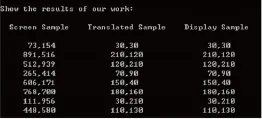
图3 校准算法优化后的测试

如果采用优化算法对上述一系列采样点进行校准，则得到的结果如图3所示。对比右边两列坐标可知，通过优化算法校准之后，计算值“Translated Sample”与理论值“Display Sample”的近似度大为提高，极大程度上提高了校准精度。

5 结论

电阻式触摸屏在安装过程中不可避免的存在机械误差，因此很多应用触摸屏的系统启动后，进入应用程序前先要执行校准程序。本文针对电阻式触摸屏分析了基本线性校准算法，在此基础上提出了一种优化的校准算法，并以嵌入式开发板为硬件平台，对校准算法进行了测试，实验结果表明，优化的校准算法有效的提高了触摸屏的校准精度，为触摸屏校准提供了一种可行实用的途径。

[1] 冯菁, 马胜前, 王科宁, 等.一种电阻式触摸屏机械安装误差的校正方法[J].制造业自动化, 2011(33): 26-27.

[2] 宋学瑞, 蔡子裕, 段青青.触摸屏数据处理算法[J].计算机工程, 2008(34): 256-257.

[3] 杨莉, 蒋奇良.拉格朗日插值算法在触摸屏校准中的应用[J].机电技术, 2011(4): 8-9.

[4] 万厚冲, 孙超云.电阻式触摸屏数据校准的一种补偿算法[J].福建电脑, 2010(2): 64.

[5] 谭翀.电阻式触摸屏校准算法的研究与设计[J].微计算机信息, 2010(26): 35-37.

[6] 罗勇刚, 夏定纯.电阻式触摸屏的校准与应用研究[J].武汉科技学院学报, 2007(20): 47-49.

[7] 王丁, 闫瑶, 张廷宇.触摸屏校准的一种通用算法[J].自动化技术与应用, 2008(27): 116-117.

[8] 盛占石, 王楚华, 周新云.基于ARM7嵌入式系统中触摸屏的设计和研究[J].电测与仪表, 2008(45): 61-63.

[9] 王党利, 马保吉, 宁生科.电阻触摸屏误差分析及加速度模型的数据处理[J].陕西理工学院院报(自然科学版),2009(25): 15-19.