焊接变位机有限元模态分析

2012-07-04刘广亮李向东马士国

制造业自动化 2012年7期

杨东，刘广亮，李向东，马士国

YANG Dong, LIU Guang-liang, LI Xiang-dong, MA Shi-guo

（山东科学院自动化研究所山东省机器人与制造自动化技术重点实验室，济南 250014）

0 引言

焊接生产的机械化和自动化可以有效提高焊接质量和效率，降低工人的劳动强度。焊接变位机[1]作为一种焊接辅助装备，是实现焊接生产机械化和自动化的重要组成部分，焊接变位机的工作性能将直接影响焊接质量。焊接变位机的工作性能与其动态性能关系非常密切，其动态性能（振动、噪声和稳定性等）是影响其工作性能和焊件质量的重要指标。

为了避免变位机在工作时发生共振或者其他有害振型，需要确定变位机系统的固有频率。本文通过有限元的分析方法[2,3]，基于ANSYS软件对焊接变位机进行有限元模态分析，得到了其低阶固有频率和对应主振型，为焊接变位机的结构优化提供参考，同时也为其故障诊断提供了方法。

1 有限元模型建立

1.1 焊接变位机实体造型

焊接变位机的结构形式可分为三种：伸臂式、座式和双座式。本文研究对象为一种伸臂式焊接变位机，如图1所示，其结构主要由回转工作台，伸臂，转轴和机座组成。

在进行有限元模态分析时，需采用适当的简化和等效原则把焊接变位机简化为利于分析的模型，以降低计算量、提高计算速度。简化的原则是，既要对分析对象进行适当简化以便于计算，又要确保分析对象的主要力学性能不发生变化。本分析删除变位机上电机等次要零部件和倒角、螺栓、螺栓孔等微小特征，简化后的模型如图2所示。

图1 焊接变位机

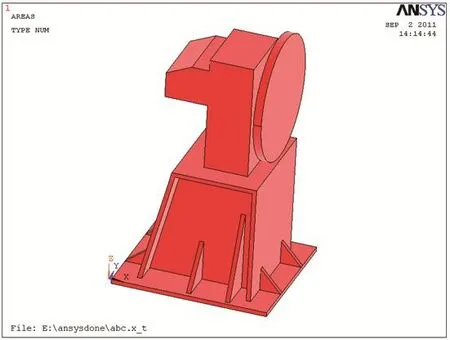
图2 焊接变位机简化模型

1.2 有限元模型建立

有限元模型建立的基本思想是将结构进行离散化，即把连续的集合体离散成无限个单元体。模型建立的过程主要包括：前处理（选择单元、材料以及网格划分等）、求解、后处理（分析结果的输出）[4]。

焊接变位机由钢结构焊接而成，其材料属性为：弹性模量207GPa；泊松比0.3；密度7.8g/cm3。充分考虑网格精度、计算速度等因素，本分析采用三维实体单元SOLID186进行网格划分，单元边界尺寸30mm。划分好网格的模型如图3所示，共有56985个单元，110405个节点。

图3 网格划分模型

2 焊接变位机模态分析

2.1 模态分析理论

模态分析用于确定设计结构或机器部件的固有频率和振型等振动特性。可以作为其他动力学问题分析的起点，如瞬态动力学分析、谐响应分析和谱分析，也是模态叠加法谐响应分析或瞬态动力学分析所必需的前期分析过程[5]。

为刚度矩阵；

为第i阶模态的振型向量（特征向量）；为质量矩阵；

wi为第i阶模态的固有频率，wi2为特征值。

多自由度系统的振动，可分解为n个单自由度的间歇真的的叠加。

2.2 模态分析结果

系统的各阶固有振型中，低阶振型对系统结构的振动影响较大，因此，对结构的动态性能影响也最大。本文对变位机进行模态分析时求得其前十阶固有频率，并对其前四阶主要振型进行说明。

求解后，得到焊接变位机的前十阶固有频率

如表1所示，前四阶模态振型如图4～图7所示。

表1 有限元计算结果

图4 焊接变位机第一阶振型

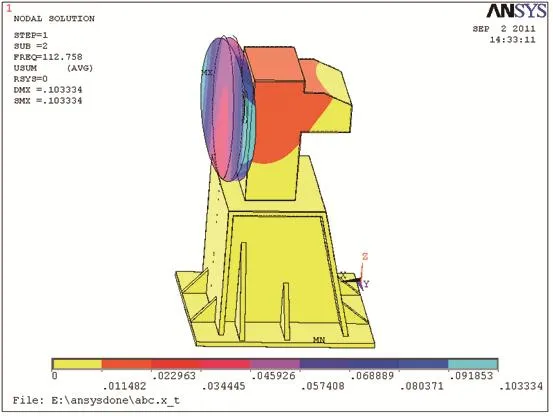
图5 焊接变位机第二阶振型

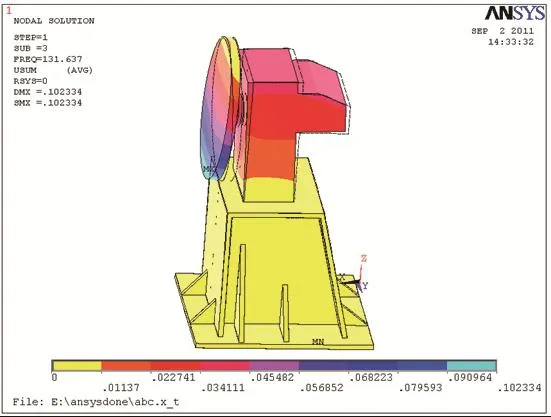
图6 焊接变位机第三阶振型

图7 焊接变位机第四阶振型

根据计算结果，焊接变位机第一阶模态振型为：回转工作台绕水平轴线翻转，伸臂前后方向倾斜，最大振动变形位置发生在回转工作台顶部。第二阶模态振型为：回转工作台绕垂直轴线旋转，伸臂前后方向倾斜，最大振动变形位置发生在回转工作台的左右两侧。第三阶模态振型为：回转工作平台绕水平轴翻转，伸臂前后方向倾斜，最大振动变形位置发生在回转工作台底部。第四阶模态振型为：回转工作台绕垂直轴旋转，系统顶部上下振动，最大变形位置发生在旋转工作台左右两侧和变位机顶部位置。

从计算结果看出，焊接变位机固有频率主要分布在100～450Hz之间。其最大振动幅值点主要发生在回转工作台上下左右四个顶点处，可采用增大回转轴刚度或添加加强筋等方法减小其振动。