基于DSP的FFT算法实现

艾 红，常青青，邓大伟

（北京信息科技大学 自动化学院，北京 100192）

0 引言

快速傅立叶变换（FFT）在雷达、通信、电子对抗和电力系统等领域有广泛应用，特别是在电力系统的谐波检测中，FFT几乎是唯一可行的检测方法。通常提高FFT运算速度有两种途径：改进FFT算法本身和改进运算工具。现阶段提高FFT算法本身非常困难，一般方法致力于改进运算工具。数字信号处理器DSP 是一种可编程的高性能处理器。文中充分利用TMS320F2812 DSP强大的数据处理能力，实现了FFT运算，并提高了运算速度。

1 系统硬件结构

系统设计以TMS320F2812处理器为核心，辅以外围电路构成。DSP负责模拟输入信号数据采集以及FFT算法实现。外围电路包括电源转换电路，时钟电路，复位电路以及外部RAM等。系统的硬件整体结构如图1所示[1]。对信号进行FFT变换，首先要对模拟信号采样将其转换为数字信号。输入的连续模拟信号经信号调理电路后输出到DSP的ADC模拟输入通道，经过ADC数据采集，模数转换的结果存放于ADC结果寄存器中。信号调理电路主要是为了信号的抗混叠滤波以及电路阻抗的匹配 。信号调理电路对输入信号进行调理处理，包括信号的滤波、跟随输出以及信号的稳定。DSP对采集的数字信号进行FFT运算处理，同时对运算结果进行相应的数据显示和数据存储。

图1 系统的硬件整体结构图

2 FFT算法原理

FFT是离散傅立叶变换（DFT）的快速运算，是数字信号处理的基础。因为有些信号在时域很难看出特性，使用FFT将其变换到频域，就会很容易看出其特性。DFT算法的基本公式为[3]：

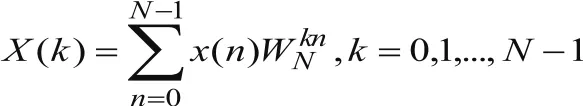
FFT算法是不断地把长序列的DFT分解成几个短序列的DFT，并利用的周期性和对称性减少DFT的运算次数。设序列x(n)的长度为N(N=2M,M为任意正整数)，按n的奇偶把x(n)分解成两个N/2点的子序列：

由此可见，若将任何一偶数点序列按下标的奇偶性分成两个子序列，则原序列的DFT可由两子序列的DFT线性组合得到。运算流图如图2所示。

图2 运算流图

图3 蝶式运算流图

其中，A和B的距离称为翅尖距。这种方法和直接进行DFT计算相比较，运算量减少一半。按照这种分解运算的思想，将X1(k)和X2(k)继续向下分解，直到最后变为一点序列，此时的运算量大大减小。以8点序列X(n)的FFT运算为例：

蝶式运算流图如图3所示。比较FFT和DFT的运算量。假设序列点数为N，且有N=2L,当使用FFT进行运算时，计算过程中只有蝶式运算，它的复数乘法运算量为，复数加法运算量为；直接进行DFT运算时，复数乘法和复数加法的运算量均为N2。由此可见，FFT运算确实大大减小了DFT的运算量。

由图3可以看出，若想得到顺序正确的频域序列X(k)，必须对时域序列进行重新排序。这里先说明比特逆序的概念：设存储地址m,其二进制数（设m=2L）为m=(m1m2m3),若有=（m3m2m1），则称为m的L位比特逆序列。若将图4中的输入时域序列下标转换成二进制，依次是：000,100,010,110,001,101,011,111；而原时域序列下标转换成二进制依次是:000,001,010,011,100,101,110,111，将两者对比可发现，输入时域序列下标就是原时域序列下标的比特逆序。所以FFT蝶式运算的第一步就是对时域序列进行比特排序。

3 系统软件实现以及结果分析

3.1 FFT程序实现

FFT算法主要包括比特逆序、蝶式权值的计算、各级的蝶式运算以及FFT序列的输出。程序中涉及到复数的运算，由于计算机无法处理复数，故而将复数拆为实部和虚部，只需计算出实部和虚部的数值即可。程序设计将蝶式权w[i]拆分为实部pr[i]和虚部pi[i]，将参与各级蝶式运算的序列拆分为实部fr和虚部fi。复数进行加法运算时需将两复数的实部与实部、虚部与虚部对应相加即可，例如w[i]+w[i+1],所得的和的实部为pr[i]+pr[i+1]，虚部为pi[i]+pi[i+1]；而复数的乘法，相对来说有些复杂，不再是简单的虚部和实部各自相乘,例如w[i]×w,所得的乘积的实部为pr[i]×pr+pi[i]×pi，虚部为:(pr[i]+pi[i])×(pr+pi)-( pr[i]×pr+pi[i]×pi)。该程序执行的是128个点的FFT运算，共有7级蝶式运算，每个蝶式权都可看作是的n次方，所以在一个循环内即可计算出所有的蝶式权。每级蝶式运算计算出新的序列值代替该级的输入序列值，这样避免了开辟新的存储空间，有效地节省了存储空间。

FFT算法程序设计如下所示：

Uint16 ConversionCount;

Uint16 px[128];

Uint16 pz[128];

void kfft(pr,pi,n,k,fr, fi ,l,il)

{ Uint16 n,k,l,il;

double pr[],pi[],fr[], fi [];

int it,m,is,i,j,nv,l0;

double p,q,s,vr,vi,poddr,poddi;

for (it=0; it＜=n-1; it++)

{ m=it;

is=0;

for (i=0; i＜=k-1; i++)

{ j=m/2;

is=2*is+(m-2*j);

m=j;}

fr[it]=pr[is];

fi[it]=pi[is]; //此循环为比特逆序的实现，pr、pi是原序列的实部与虚部

} //fr、 fi 是排完序后的序列

pr[0]=1.0; pi[0]=0.0;

p=6.283185306/(1.0*n);

pr[1]=cos(p);

if (l!=0) pi[1]=-pi[1];

for (i=2; i＜=n-1; i++)

{ p=pr[i-1]*pr[1];

q=pi[i-1]*pi[1];

s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);

pr[i]=p-q;

pi[i]=s-p-q;} //此循环为权值运算实现

for (it=0; it＜=n-2; it=it+2) //it是序列下标，

在第一级蝶式运算中

//相邻的两个运算蝶下标相差2

{ vr=fr[it]; vi= fi [it];

fr[it]=vr+fr[it+1]; //第一级蝶式运算中相邻两个数值进行加减运算

fi [it]=vi+ fi [it+1];

fr[it+1]=vr-fr[it+1];

fi [it+1]=vi- fi [it+1];} //此循环为第一级蝶式运算，该级中的蝶式权均为1

m=n/2; nv=2;

for (l0=k-2; l0＞=0; l0--) //除去第一级，还有六级蝶式运算

{ m=m/2; nv=2*nv; // 同一级相邻的两个蝶式运算中数值的下标相差为nv

for (it=0; it＜=(m-1)*nv; it=it+nv) //it仍为数值的下标

for(j=0;j＜=(nv/2)-1;j++)

{ p=pr[m*j]*fr[it+j+nv/2]; // nv/2为蝶式运算的翅间距

q=pi[m*j]*f i [it+j+nv/2];

s=pr[m*j]+pi[m*j];

s=s*(fr[it+j+nv/2]+f i [it+j+nv/2]);

poddr=p-q; poddi=s-p-q;

fr[it+j+nv/2]=fr[it+j]-poddr;

fi [it+j+nv/2]=f i [it+j]-poddi;

r[it+j]=fr[it+j]+poddr;

fi [it+j]=f i [it+j]+poddi; //计算出的新序列值代替输入序列值,节省了存储空间

}}} // fr、f i 分别为计算出的FFT序列的实部和虚部

3.2 运行结果

用FFT的计算公式对单一频率的正余弦信号进行变换，可以得出单一频率的信号在频域表现为在其正负频率点上的两个脉冲。根据单频信号的这一特性可验证上述程序是否正确。将单一频率的正弦波信号接入硬件系统，打开图形观察窗口，将观察点数设置为128点，即可观察到如图4所示的波形。

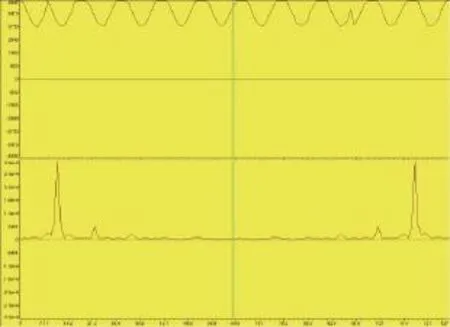
图4 时域正弦波的FFT运行结果

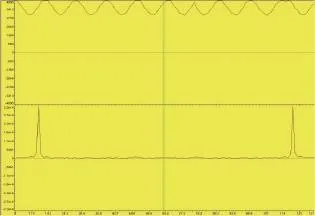
图5 改善后的FFT运行结果

图4中上半部分波形为输入的时域正弦波，下半部分波形为经过变换后的频域波形。在图4中，由于产生的模拟信号伴有噪音，导致信号频率不单一，故而在信号的频域中，除了信号对应的频率点有脉冲外，其它频率点处也有较弱的脉冲。

对输入信号的频率进行调整，使信号的组成频率尽可能单一，可以得到更好的波形，如图5所示。可以看到在信号对应的频率点有脉冲，其它频率点的振幅为0，与理论推导结果一致，由此可验证程序设计的正确性。

4 结论

FFT是声学、图像和信号处理等领域中一种重要的分析工具，文中阐述了硬件结构图和信号调理电路。详细介绍了FFT算法原理，采用C语言编写程序实现了FFT算法。程序运行结果表明TMS320F2812 DSP实现FFT运算速度快，精度高[4]。

[1] 贾玮,杨录,张艳花.基于TMS320VC5416的FFT算法的实现[J].山西电子技术,2009,2:11-13.

[2] Rright Hert. Rapid algorithms of digital signal processing[M].Beijing,Electronic Industrial Press,2002.

[3] 胡广书.数字信号处理[M].北京:清华大学出版社,2003.

[4] 苏奎峰,吕强,耿庆锋,陈圣俭.TMS320F2812原理与开发[M].北京:电子工业出版社,2005.