抛光机器人轨迹连续性规划与仿真

张 栋，贠 超，何竞择，宋 涛

（北京航空航天大学 机械工程及自动化学院，北京 100191）

0 引言

随着对产品质量要求的提高，在更多产品中使用抛光加工以提高表面质量。目前，复杂几何形状工件的抛光工艺主要由人工完成。人工抛光加工，劳动繁重，环境恶劣，生产效率低，且对工人经验要求较高，产品一致性差[1,2]。

与数控机床抛光相比，机器人抛光更具柔性和灵活性，适合复杂曲面的抛光操作[3]。而通用机器人在结构刚度上表现欠佳，不能完全满足抛光加工力较大的要求，且存在一定的振动，因而抛光质量，效率和适用范围受到制约[4]。而对专用的抛光机器人进行轨迹规划研究，将有助于提高其加工能力和质量，减少对示教的依赖。

1 抛光机器人结构分析

本文所述的抛光机器人系统，专为复杂曲面的抛光加工设计，同时具备了机器人运动灵活和机床结构刚度高的优点，在较大抛光力作用下，较高速的抛光加工中，表现突出。从而可以适应较复杂曲面，获得较高的质量、精度和效率。

该抛光机器人系统为两工位同步运动的3P3R型，6自由度机器人，如图1所示。其中，抛光轮安装部分具有2个自由度，分别是沿竖直方向的移动自由度Z，以及与Z轴和抛光轮旋转轴线均垂直的转动自由度A；工件装卡结构部分具有4个自由度，分别是水平面内相互垂直的移动自由度X和Y，轴线沿竖直方向的转动自由度B，以及轴线与B轴垂直的转动自由度C。

图1 抛光机器人结构

另外，抛光轮轮轴的轴承座，通过滑块导轨，安装于抛光轮支架上，在振动汽缸的带动下，可沿抛光轮旋转轴线方向振动。振动频率在每分钟30～200次，以适应加工要求。抛光轮会随着抛光加工的进行发生磨损，本机安装的抛光轮许用直径为300mm～600mm。

为获得较理想的灵活空间，需使用抛光轮上不同位置进行加工，所以，抛光加工点所在的扇区位置，被认为是一个可由操作人员指定的自由度。而变换扇区由人为设置，即只能设定离散的值，即会造成实际抛光轨迹的不连续。为解决因扇区改变造成的不连续，首先，应尽量避免同一工件加工中不必要的扇区更改，即尽量通过A, B,C, X, Y, Z等6个自由度调节机器人姿态，完成抛光作业；其次，在抛光路径上，扇区改变时，连续插入多个示教补充点，且这些点应为工件坐标系下一定规律曲线上的点。

2 抛光机器人运动学分析

2.1 D-H方法

为描述相邻杆件问平移和转动的关系，Denavit和Hanenberg于1955年提出了一种为关节链中的每一杆件建立附体坐标系的矩阵方法。对于旋转关节关节角是关节变量，其余参数固定不变；对于移动关节，偏置是关节变量，其余参数固定不变。

2.2 建立D-H坐标系

通用的6R型工业机器人一般以世界坐标系作为第0坐标系，进行建模。而本抛光机器人的自由度分列于工件和工具两部分，为研究抛光加工点，在工件坐标系内的运动，以工件坐标系作为第0坐标系。原点建于BC轴交点上。并根据抛光机器人结构尺寸，按照D-H方法依次建立各坐标系。为描述抛光加工时所使用的抛光轮上弧段的区域，建立第7坐标系。如图2所示。

相应各杆件的结构参数和运动参数，如表1所示。与该套建系方案相对应，须规定各关节的正方向及移动或转动范围。则第8系原点为加工点，Z8指向加工法向，X8指向抛光速度方向。

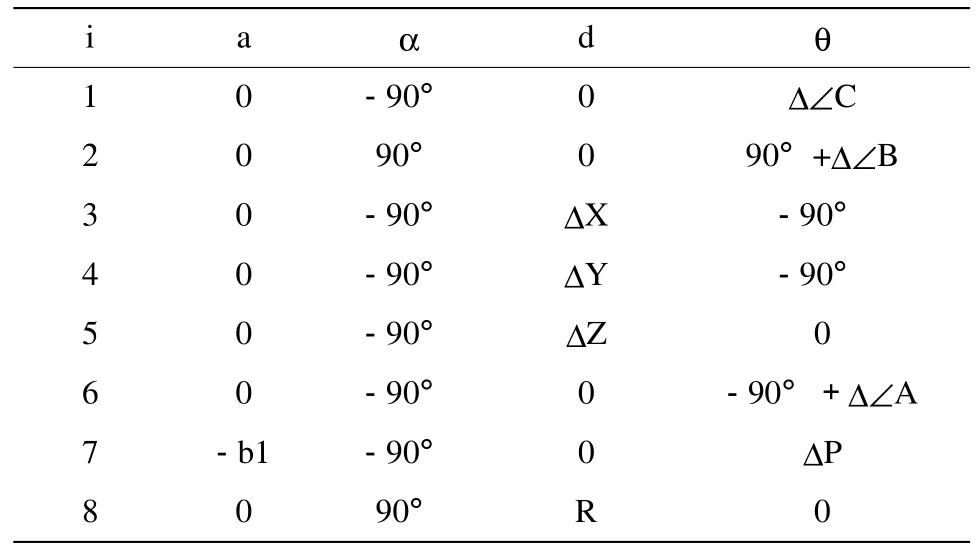
表1 抛光机器人D-H参数表

2.3 机器人运动学正解

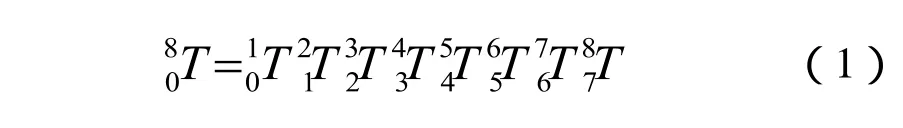
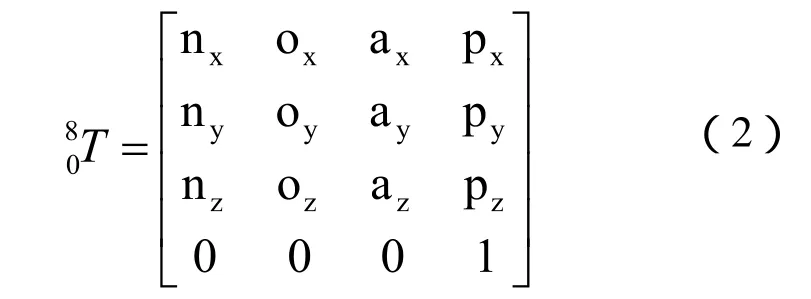
图2 抛光机器人D-H建模图

解得各项如下：

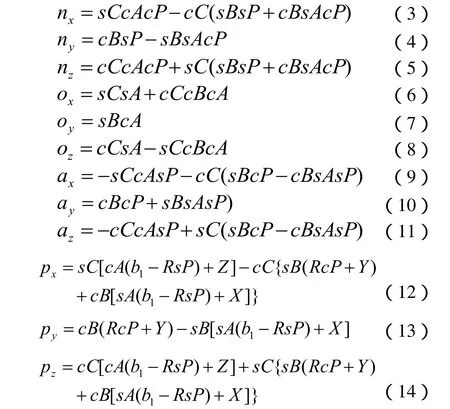
依次绕固定坐标系的X0，Y0，Z0轴旋转γ角，β角，α角。可由矩阵形式描述为：

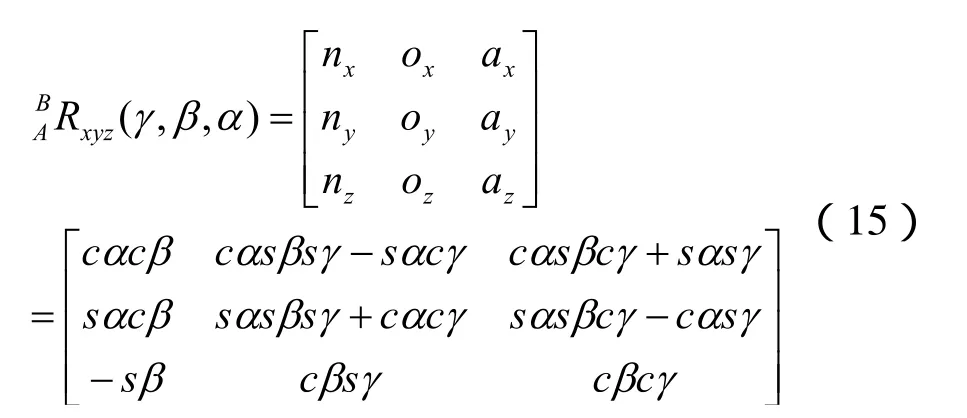
则有，在cosβ≠0时，

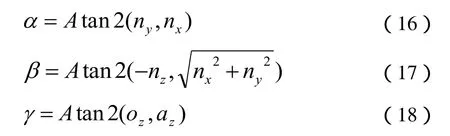
所求得的px，py，pz和α，β，γ即可描述抛光加工点的位置和姿态。

2.4 机器人运动学逆解

在已知抛光点在工件坐标系中的位置，法线方向和抛光速度方向的条件下，要求得各关节的移动或转动量，就需要求解运动学的逆解。对机器人运动学正解，进行观察求解可得：

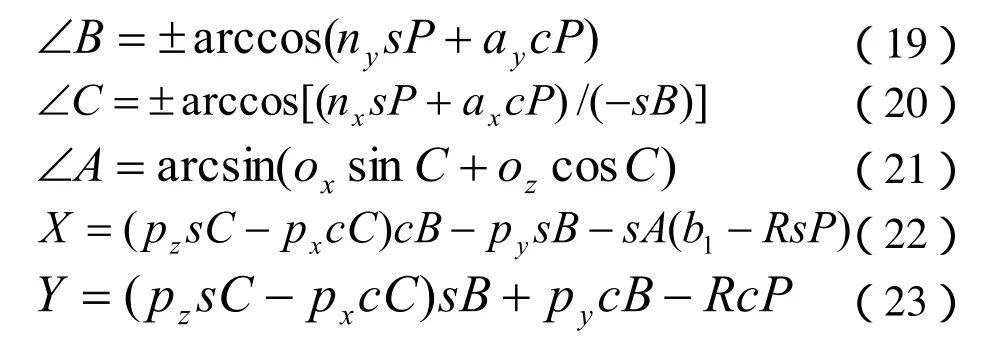
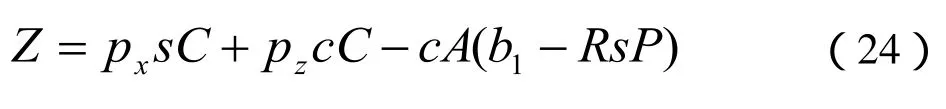
式（19）!式（24）中，b1＝51.5。

3 三次参数曲线插值

波音公司的弗格森（1963）首先引入参数三次方程，用于在飞机设计中进行曲线和曲面的定义。

参数三次（parametric cubic）曲线，简称PC曲线，

用幂基表示：

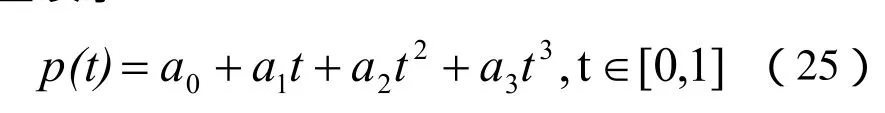
将式（25）对参数t求导：

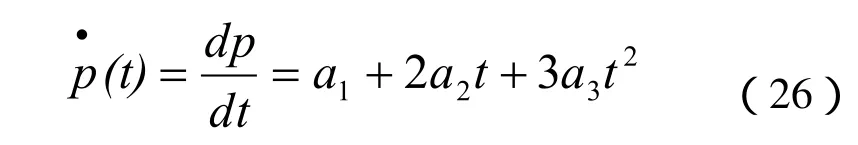
用t＝0，1分别代入式（25）和式（26）中，有

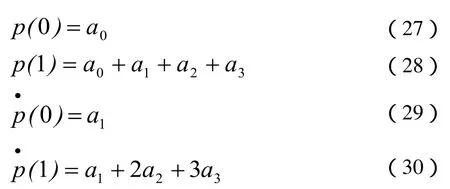
其矩阵形式即：

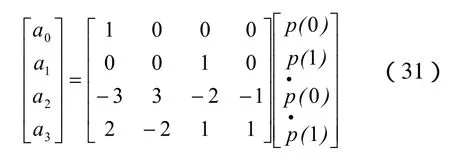
将式（25）代入式（31）。可以得到用两断电及其切矢表示的参数三次曲线段：

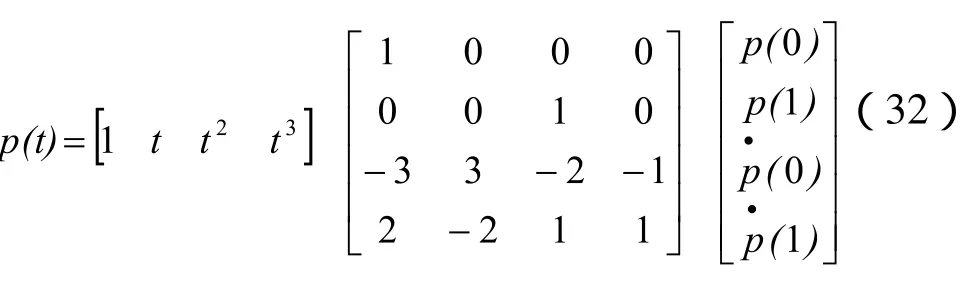
某抛光轨迹，共有n个点，其中第i个点，当1＜i＜n时，令该点处的导数为线段（pi-1，pi）和线段（pi，pi+1）的斜率的均值，则有：

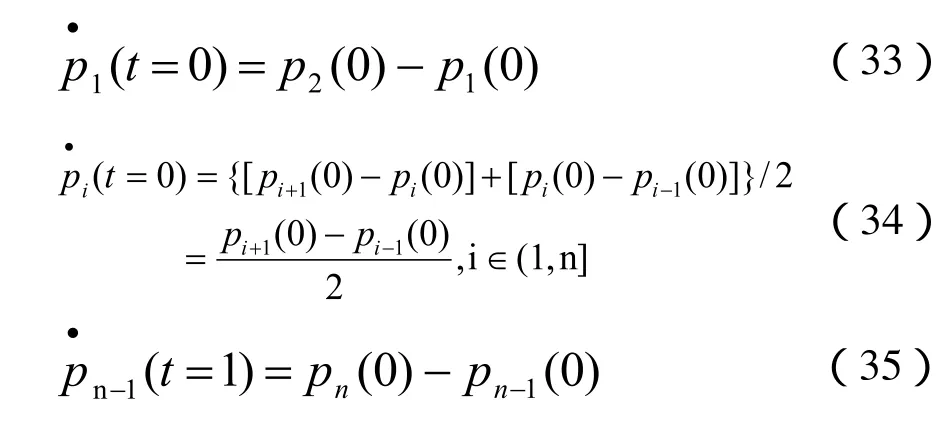
即可得到一条由n-1段参数三次曲线拼得的一条连续可微的曲线段（p1，p2，…，pn）。

4 轨迹规划仿真

以一条35个点的抛光示教轨迹为例，根据上述三次参数曲线插值的方法，对该轨迹进行插值。令式（32）至式（35）中 p 分别以上述px，py，pz和?，?，?为研究对象，带入三次参数曲线方程中，进行插值计算，获得响应的插值点，同时包括加工点的位置和角度信息。

利用matlab进行仿真，可以得到松弛方法获得的抛光加工轨迹如图3中左图所示，较大程度上偏离了工件表面，抛光轮吃入量时大时小，尤其在工件表面曲率较大处较为明显。而图3中右图所示，为采用三次参数曲线插值方法获得的加工路径，可以看出各加工点均匀平滑，且抛光加工的方向和主速度方向变化连续。

在X-Y平面和X-Z平面内观察轨迹，如图4和图5所示，可明显体现出应用三次参数曲线插值的方法，规划得到的抛光加工轨迹与工件表面契合程度高，轨迹光顺，变化连续与实际工件表面最大距离小于1mm；而松弛的抛光轨迹在示教点之间运动规律随机性较大，特别是在曲率变化较大的局部偏离加工面的现象严重，与工件表面点最大偏离超过4毫米，将严重影响加工质量。

当控制条件为最大关节速度恒定时，各关节驱动电机中转速最高的电机的转速为定值，则两点间的运行时间：

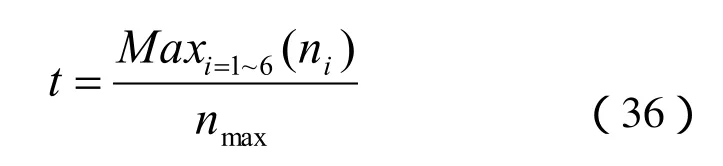
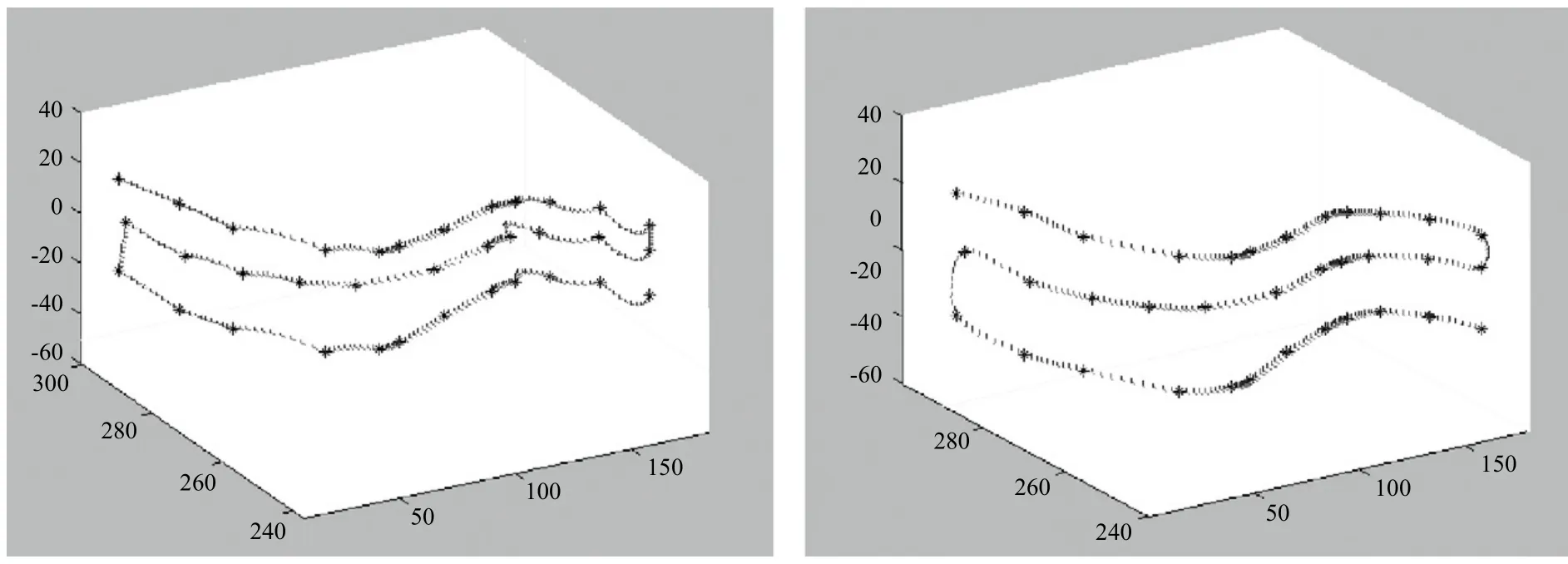
图3 轨迹连续控制方法与松弛位置方法的轨迹对比

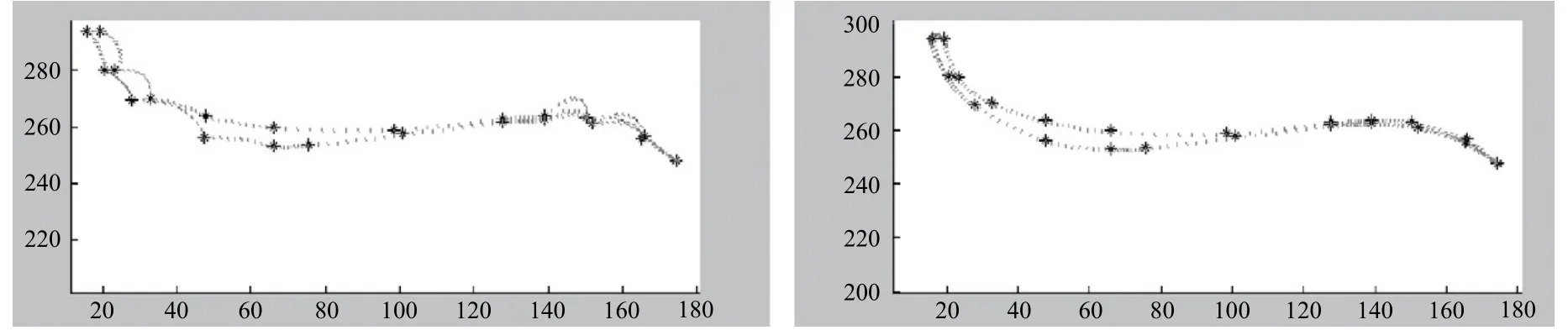
图4 X0-Y0平面内轨迹投影对比（横轴为X0，纵轴为Y0，单位mm）

图5 X0-Z0平面内轨迹投影对比（横轴为X0，纵轴为Z0，单位mm）

在较小长度范围内，认为两点间的抛光轨迹为直线，则有抛光轨迹速度

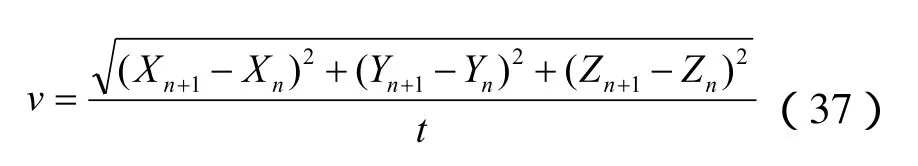
采用轨迹连续的控制策略时，已知相邻两点间的距离和各关节中的发生最大位移量的关节。所以，在速度过快时，可以通过改变nmax，以限制最高速度，实现进给运动的速度稳定。图6为伺服电机最高转速为1200r/min时，在工件坐标系内，抛光加工点移动速度的对比。

松弛的抛光轨迹，速度变化突然，波动范围大，最高速度达到270mm/s，大大超过了抛光加工所要求的进给速度。应用连续轨迹控制方法，速度波动范围较小。变化相对连续。基本在50mm/s至80mm/s速度范围内，符合工艺要求。

5 结论

本文在抛光机器人的结构分析、运动学分析和轨迹规划等三个方面的结论如下：

1)专用型抛光机器人，结构刚度高、运动灵活、适应复杂曲面和加工质量高；

2) 应用D-H方法，获得运动学正反解，以实现对机器人姿态和加工轨迹的控制；

3）基于三次参数曲线，设计轨迹规划方法，以实现抛光机器人加工轨迹，位置和姿态连续变化的规划，解决各示教点间抛光轨迹偏离和加工姿态不理想的问题。

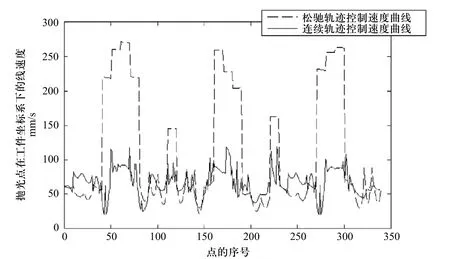
图6 工件坐标系内抛光加工点移动速度对比曲线图

[1] 洪云飞, 李成群, 贠超. 用于复杂空间曲面加工的机器人磨削系统[J]. 中国机械工程, 2006, 8(17): 150-152.HONG Y F, LI C Q, YUN C. Robot Grinding System for 3D Complex Surface Processing[J]. China Mechanical Engineering, 2006, 8(17): 150-152(in Chinese).

[2] S. J. Go, M. C. Lee, and M. K. Park, “Development of Automatic Polishing System and Fuzzy-Sliding Mode Cont-rol Based on Genetic Algorithm”, Proc. Of the American Control Conference, pp.25-27, 2001.

[3] LIAN G, SUN z Q, MU c D. Optimal motion planning passing through kinematic singularities for mbet arm8[C]IROS 2006. Beijing: IEEE Press, 2006: 4349-4351.

[4] R-S Lin, Y Koren, Efficient tool-path planning for machining free-form surfaces, Journal of Engineering for Industry, Transactions of the ASME. vol.118, pp. 20-28,april, 1996.

[5] 张红强, 章兢, 王耀南, 等. 机器人关节空间B样条轨迹设计的混沌优化[J]. 电机与控制学报, 2007, 1l(2): 174-177.

[5] ZHANG H Q, ZHANG J, WANG Y N, et a1. Chaos optimization0f B-splines path plannihg for robot in joint space[J]. Electric Machines and Control, 2007, 1l(2): 174-177. (in Chinese).

[6] Chen, Y. -Ch.: Solving Robot Trajectory Planning Problems with Uniform Cubic B-Splines. Optimal Control Applications and Methods 12 (1991), pp. 247-262.

[7] A. I. F. Vaz and E. M. Fernandes, “Tools for robotic trajectory planning using cubic splines and semi-infinite programming,” in Recent Advances in Optimization, A.Seeger, Ed. Springer, 2006, pp. 399-413.

[8] H. Chen, N. Xi, Z.Wei, Y. Chen, and J. Dahl, “Trajectory integration for a surface with multiple patches,” in Proc.IEEE Int. Conf. Robotics and Automation, 2003, pp. 3984–3989.