Classification of Phase Portraits of Z2-Equivariant Planar Hamiltonian Vector Fields of Degree 7(Ⅱ)*
2012-07-02LIYanmei
LI Yanmei
(Department of Mathematics,Chuxiong Normal University,Yunnan Chuxiong,675000,China)
The phase portraits of planar Zq-equivariant Hamiltonian vector fields of degree 7 are much more complicated than that of degree 5,and only a few vector fields of degree 7 have been discussed[1—5].In this paper,we will classify the phase portraits of a new planar Z2- equivariant Hamiltonian vector field of degree 7

where k is a parameter with k>0.
1 Qualitative Analysis of the Singular Points
Because the system(1)has the property of Z2- equivariant,namely,the phase portrait is the same when it rotates π clockwise,so we only need to study the singular points in the first and second quadrants.
The Jacobian of this system is

in which

Discussing the Jacobians of these singular points,we can obtain the following results without difficulty:

Obviously,the function H(x,y)satisfies the equality H(x,y)=H(x,0)+H(0,y),and we can readily obtain
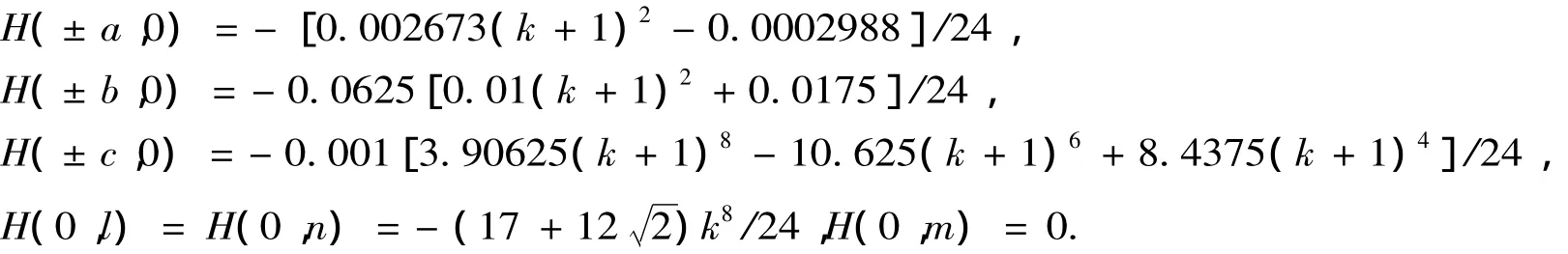
2 Phase Portraits of the System(1)
The Hamiltonian of the system(1)is
H(x,y)= [3x8- (k2+2k+2.36)x6+(0.51k2+1.02k+0.645)x4- 0.0675(k+1)2x2
Comparing the Hamiltonians of the singular points,we get the following results.
Theorem 2
(1)If0<k<0.239066,the phase portrait of the system(1)can be shown as Fig.1(1).
(2)If k=0.239066,the phase portrait of the system(1)can be shown as Fig.1(2).
(3)If 0.239066<k<0.255214,the phase portrait of the system(1)can be shown as Fig.1(3).
(4)If k=0.255214,the phase portrait of the system(1)can be shown as Fig.1(4).
(5)If 0.255214<k<0.2806248,the phase portrait of the system(1)can be shown as Fig.1(5).
(6)If k=0.2806248,the phase portrait of the system(1)can be shown as Fig.1(6).
(7)If 0.2806248<k<0.28217,the phase portrait of the system(1)can be shown as Fig.1(7).
(8)If k=0.28217,the phase portrait of the system(1)can be shown as Fig.1(8).
(9)If 0.28217<k<0.282535,the phase portrait of the system(1)can be shown as Fig.1(9).
(10)If k=0.282535,the phase portrait of the system(1)can be shown as Fig.1(10).
(11)If k >0.282535,the phase portrait of the system(1)can be shown as Fig.1(11).
Proof
We denote H(0,0),H(± a,0),H(± b,0),H(± c,0),H(0,l),H(0,m),H(0,n),H(± a,l),H(± a,m),H(± a,n),H(± b,l),H(± b,m),H(± b,n),H(± c,l),H(± c,m),and H(± c,n)by h00,ha0,hb0,hc0,h0l,h0m,h0n,hal,ham,han,hbl,hbm,hbn,hcl,hcmand hcm,respectively.Obviously,we have hxy=hx0+h0y,h0l=h0n,h0m=0.
(1)If k=0.229005,then hcl=ha0.Hence,when 0 < k < 0.239066,the Hamiltonians of the singular points satisfy the relations hal=han<ha0=ham≤hcl=hcn<hc0=hcm<hbl=hbn<hb0=hbm<h0l=h0n<h00=h0m,so the phase portrait can be shown as Fig.1(1).
(2)When k=0.239066,we have hcm=hbl,and the Hamiltonians of the singular points satisfy the relations hal=han<hcl=hcn<ha0=ham<hc0=hcm=hbl=hbn<hb0=hbm<h0l=h0n<h00=h0m,so the phase portrait can be shown as Fig.1(2).
(3)When 0.239066<k<0.255214,the Hamiltonians of the singular points satisfy the relations hal=han<hcl=hcn<ha0=ham<hbl=hbn<hc0=hcm<hb0=hbm≤h0l=h0n<h00=h0m,so the phase portrait can be shown as Fig.1(3).
(4)When k=0.255214,we get ha0=hbl,and the Hamiltonians of the singular points satisfy the relations hal=han<hcl=hcn<ha0=ham=hbl=hbn<hc0=hcm<h0l=h0n<hb0=hbm<h00=h0m,so the phase portrait can be shown as Fig.1(4).
(5)When0.255214<k<0.2806248,the Hamiltonians of the singular points satisfy the relations hal=han<hcl=hcn<hbl=hbn<ha0=ham<hc0=hcm<h0l=h0n<hb0=hbm<h00=h0m,so the phase portrait can be shown as Fig.1(5).
(6)When k=0.2806248,we obtain aa0=hc0,and the Hamiltonians of the singular points satisfy the relations hal=han=hcl=hcn<hbl=hbn<ha0=ham=hc0=hcm<h0l=h0n<hb0=hbm<h00=h0m,so the phase portrait can be shown as Fig.1(6).
(7)When 0.2806248<k<0.28217,the Hamiltonians of the singular points satisfy the relations hcl=hcn<hal=han<hbl=hbn<hc0=hcm<ha0=ham<h0l=h0n<hb0=hbm<h00=h0m,so the phase portrait can be shown as Fig.1(7).
(8)When k=0.28217,we obtain ha0=hol,and the Hamiltonians of the singular points satisfy the relations hcl=hcn<hal=han<hbl=hbn<hc0=hcm<ha0=ham=h0l=h0n<hb0=hbm<h00=h0m,so the phase portrait of the system(1)can be shown as Fig.1(8).
(9)If 0.28217<k<0.282535,the Hamiltonians of the singular points satisfy the relations hcl=hcn<hal=han<hbl=hbn<hc0=hcm<h0l=h0n<ha0=ham<hb0=hbm<h00=h0m,so the phase portrait of the system(1)can be shown as Fig.1(9).
(10)If k=0.282535,we get h0n=hc0,and the Hamiltonians of the singular points satisfy the relations hcl=hcn<hal=han<hbl=hbn<hc0=hcm=h0l=h0n<ha0=ham<hb0=hbm<h00=h0m,so the phase portrait of the system(1)can be shown as Fig.1(10).
(11)If k >0.282535,the Hamiltonians of the singular points satisfy the relations hcl=hcn<hal=han<hbl=hbn<h0l=h0n<hc0=hcm<ha0=ham<hb0=hbm<h00=h0m,so the phase portrait of the system(1)can be shown as Fig.1(11).

Fig.1(1)~(11)The phase portraits of system(1)
[1]Wu Kaiteng,Cao Hongjun.Classification of phase portraits about planar quintic Z4- equivariant vector fields.Proceedings of the third international conference on nonlinear mechanics[M].Shanghai:Shanghai University press,1998:873—877.
[2]Li Yanmei.The classification of phase portraits about some Hamiltonian vector field with Z3- equivariant property [J].Journal of Yunnan Normal University,2003,23(6):5—7.
[3]Li Yanmei.The General Form and Phase Portraits of Planar Septic Hamiltonian Vector Field with Z8- Equivariant Property [J].Journal of Chuxiong Normal University,2010,25(12):32—35.
[4]Li Yanmei.The Phase Portraits of a type of Planar Septic Hamiltonian Vector Field with Z2- Equivariant Property [J].Journal of Chuxiong Normal University,2011,26(9):47—50.
[5]Li Yanmei,Hu Zhao.Classification of Phase Portraits of Z2- Equivariant Planar Hamiltonian Vector Fields of degree 7(Ⅰ)[J].Journal of Chuxiong Normal University,2012,27(6):1—4.
