三相并网逆变器比例谐振控制及其网压前馈问题分析

马 琳 金新民 唐 芬 Pedro Rodriguez 孙 凯

（1. 北京交通大学电气工程学院 北京 100044 2. 西班牙加泰罗尼亚理工大学 巴塞罗那 08222 3. 清华大学电力系统及大型发电设备安全控制和仿真国家重点实验室 北京 100084）

1 引言

近年来，基于可再生能源的分布式并网发电技术如光伏发电、燃料电池发电和风力发电等，得到了快速的发展。与传统的集中式发电系统相比，其距离用户更近，发电灵活性更高，能更充分地利用各种可用的分散存在的能源，成为了电能供应不可缺少的有益补充。作为分布式能源与电网间进行能量变换的逆变器，如何更加有效、可靠地使分布式发电系统所发出的电能并入电网具有重要的现实意义[1,2]。为此，多种新型的并网电流控制方法得到了应用[3]。

小型单相并网系统如屋顶式光伏并网系统其逆变器传统控制方式采用传统网压前馈的比例积分控制，存在着固有的静态误差等问题[4]。为克服传统控制器的缺陷，很多新型单相并网逆变器常采用比例谐振控制[5,6]作为其并网电流的控制方法，用以消除在跟随单相正弦电流指令时比例积分控制器固有的静态误差。大功率三相并网系统如风力发电，常采用基于电网电压矢量定向的比例积分（PI）控制。该并网电流控制方法，通过对旋转坐标系的 dq两个坐标分量分别控制，实现有功分量与无功分量解耦，理论上可以做到无静态误差控制[7]。除此之外，根据不同的应用条件，也涌现了其他多种控制方式[3]，例如静止坐标系控制法（Stationary Reference Frame Control）与自然坐标系控制法（Natural Frame Control）等。

基于电网电压矢量定向的同步旋转坐标系控制法，尽管已经得到了广泛应用，但是采用PI控制器对并网电流调节时，需要进行多次坐标系的旋转变换，增加了控制的复杂性和算法实现的难度；尤其对系统低次谐波进行补偿时，各次谐波分量均需进行多次复杂的高低通滤波和坐标变换，且滤除相应次的负序谐波分量时，还会使计算量加倍，加大系统控制算法实现的难度[8]，同时，在动态响应能力方面也不具优势。

本文利用比例谐振控制器能够在静止坐标系下对交流信号进行无静差调节，无需坐标旋转变换，不存在耦合项和前馈补偿项，且易于实现低次谐波补偿的特点[9]，实现了对三相并网逆变器并网电流的良好控制。

为了进一步提高静止坐标系控制的对于网压突变的抗干扰能力，降低动动过电流，作者采用了带有网压瞬时值前馈的静止坐标系控制方法。但在实验过程中发现采用此控制方式，当电网存在较大非线性负载，造成变流器共用接入点电压畸变时，静止坐标系中的网压瞬时值前馈控制环节会对整个控制造成很大的负面影响，使并网电流严重畸变时。针对该问题，作者在已有静止坐标系比例谐振控制的基础上，提出了一种采用带有比例系数的正序网压前馈控制方法，通过该方法极大提高了并网电流质量，并得到了实验验证。

2 比例谐振控制器

比例谐振（Proportional Resonant，PR）控制器理论成熟于20世纪90年代，由于其具有易于实现谐波补偿的特点，最先应用于有源滤波器及谐波补偿控制的设计当中[10]。2004年以后，开始逐渐被应用于单相及三相电流的控制之中[11]。

其思想主旨是在控制器传递函数的 jω 轴上加入两个固定频率的闭环极点，形成该频率下的谐振，从而增大该频率点的增益（理论上，谐振使得该设计频率下的增益趋近于无穷大），实现对该频率下的正弦指令信号的无差跟踪，克服了PI控制器无法无静差跟踪正弦信号的不足。如果换一个角度去思考，在三相并网逆变器的电压矢量定向控制中，是将αβ静止坐标系中的正弦量转化为了 dq同步旋转坐标系中的直流量，从而使得可以利用PI控制器完成对直流量的无静态误差的控制，这里坐标转换的条件是，得到同步旋转的角速度。在比例谐振控制中，同样需要一个谐振频率，从数学本质上讲是一致的，即得到同步旋转的角速度。比例谐振控制利用谐振控制等效省去了坐标系变换的过程，使得这种控制方法可以对特定频率的正弦指令信号进行无差跟踪。

有关比例谐振控制器的相关论文众多[4,5,9-11]，在此不再赘述，仅从其电流追踪特性上对其控制特性进行简要阐述

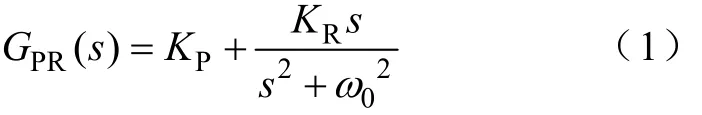
图1给出当采用比例谐振控制跟踪正弦并网电流指令的控制框图（该指令可以是单相并网电流指令，也可以是三相静止坐标系中的αβ 正弦指令，或者是三相自然坐标系中，任意一相的电流指令）。Gd(s)为逆变器传递函数，Gf(s)为滤波电感传递函数。

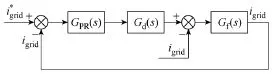
图1 电流环PR控制框图Fig.1 Current loop PR controller

采用比例谐振控制的输出电流如下

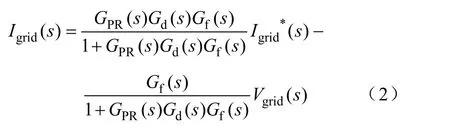
该表达式可分为两部分：第一部分，即跟随电流指令部分，从闭环伯德图2分析中可知，在跟踪正弦指令时，比例谐振控制很好的解决了稳态误差的问题。

图2 PR与PI控制器闭环伯德图Fig.2 Bode plot of closed-loop PR and PI controller

该式的第二部分为电网作用部分，由于该部分的存在，电网会对所控并网电流造成影响，也就是说实际上并网电流的误差是由控制器跟踪正弦指令所造成的误差和电网电压造成的误差两部共同组成的。从电网作用伯德图3分析中可知，比例谐振控制可以消除特定频率下电网的作用（该频率下的衰减趋近于无穷）。

图3 PI、PR控制电压扰动伯德图Fig.3 PI and PR disturbance bode plot

该式第二部分也说明了为什么在单相并网电流控制跟随正弦指令电流采用比例积分控制器时，必须加入网压前馈环节（用于消除第二部分误差），而采用比例谐振控制器可以不加入网压前馈。综上所述，PR控制器利用所加入的谐振环节，使得PR控制器在跟随正弦电流指令时，可以消除稳态误差，并且消除网压基频对并网电流的影响，从而可以省去网压前馈环节的使用。有关比例谐振控制的具体实现方法参见文献[4]。

3 静止坐标系比例谐振并网控制

比例谐振控制器不仅可以运用于单相并网系统，还可以应用于三相系统电流控制当中。传统的三相系统使用同步旋转坐标系控制，采用 PI 控制器对并网电流调节时，具有计算量大、谐波补偿困难以及控制参数选取困难等缺点。

本文作者利用比例谐振控制器能够在静止坐标系下对交流信号进行无静差调节，无需dq坐标旋转变换，不存在耦合项和前馈补偿项，且易于实现低次谐波补偿的特点，实现了对三相并网逆变器并网电流的良好控制。

以三相电压型 PWM并网变流器为例，电压与电流采样点如图4所示。

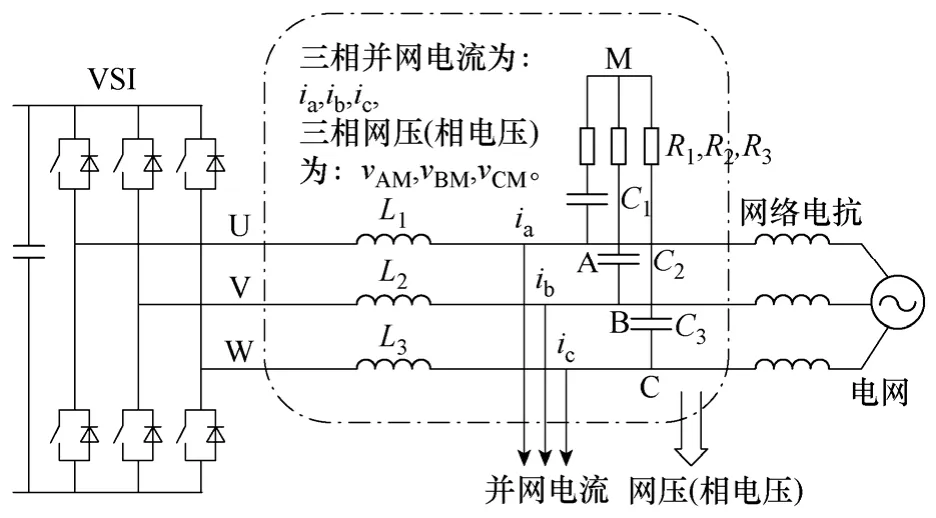
图4 网压，并网电流采样点Fig.4 The sample points of grid voltage/ current

图5给出了静止坐标系PR并网控制框图，并网控制过程简述如下：

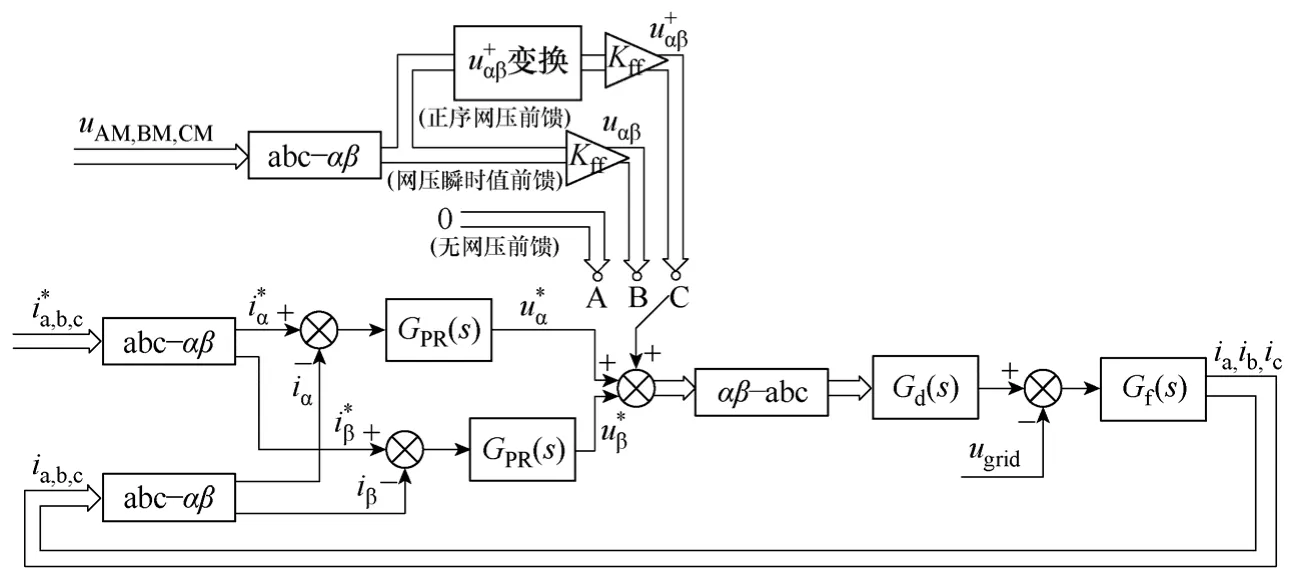
图5 逆变器并网电流控制框图 (静止坐标系PR控制)Fig.5 Control sheme of grid current injection

（1）通过外环控制或是并网功率指令计算得到并网瞬时电流值。

（4）在电流控制器输出端加入不同的网压前馈环节。方式A为无网压前馈，方式B加入瞬时网压前馈，本文所提出的方式C为加入正序网压前馈。

（5）将最终输出量由静止坐标系反变换至自然坐标系后，将所得调制波形输入 PWM比较寄存器进行脉宽调制。

正如前文所述，静止坐标系控制方法在控制理论上从消除静态误差的角度上讲可以不采用网压前馈环节[4,5]。但是，如果不加入网压前馈环节，在系统启动或网压突变时，其响应速度仍然会受到影响。因此，近年来在使用静止坐标系控制时，为了进一步提高系统的响应速度（如应对风力发电故障穿越问题），如图 5所示中 B点通路带有网压前馈静止坐标系控制法得到了应用[14]，本文将在下一节中详细讨论。

4 比例谐振控制的网压前馈

采用网压前馈控制，最直接的方式是采用如图5中B点的网压瞬时值前馈，理论上采用瞬时电压超前反馈，当变流器公用接入点(PCC)电压发生变化时，超前反馈量也同时发生变化，不会对控制造成任何负面影响；但是问题在于，考虑到A-D采样延时，处理器计算周期延时等延时，最后叠加在控制器输出量上的前馈值已经不再与当前接入点电压同步。当所并入的电网为弱电网，并存在较大的非线性负载造成接入点电压畸变的条件下，利用瞬时网压前馈控制会导致控制系统的不稳定，引入大量的谐波。

因此在本文中，提出了一种带有比例系数的正序网压前馈控制方法来改善上述的问题，该控制框图如图5中C点所示。其中，图5所示的正序分量通过二阶广义积分（Second Order Generalized Integrator，SOGI）正交计算获得，其定义矩阵见式（3），利用式（5）计算得到，具体实现过程请详见参考文献[15]。

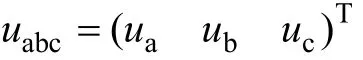
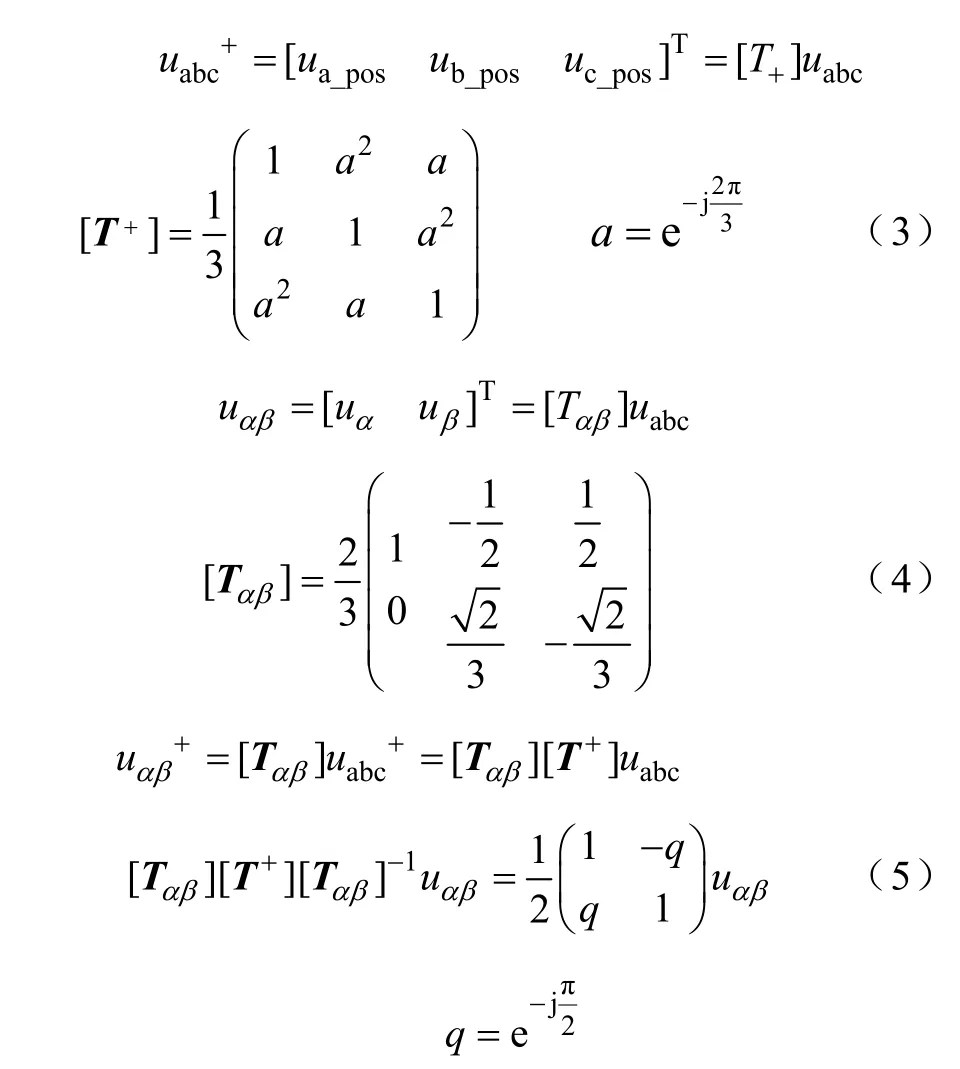
下表给出了正序分量与原信号中 1～5次谐波的对比。正序分量在包含了所有基波分量的同时，可以消除由于非线性负载所引入的3次谐波，同时弱化偶次谐波分量。式（6）给出了三相坐标系下，信号正序分量与原信号的数学表达式关系。

从结果上可以理解为：当采用正序分量作为前馈量时，实际上相当于对特定次谐波进行了滤波，同时，除计算周期外，没有引入其他额外的延时。

表 正序分量与输入量谐波对比（输入量1∠0°）Tab. Harmonic comparison

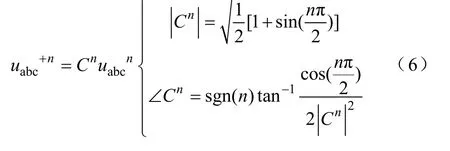
尽管如此，在接入点电压畸变严重，尤其是在并网阻抗较大时，利用正序网压前馈仍然会引入正序分量不可消除的5、13等次谐波。于是需要在动态性能与并网电流质量之间做一个取舍，这时就引入了网压前馈比例系数Kff，当需要更佳的动态性能时，增大Kff；当并网电流质量由于网压畸变不能满足要求时，降低 Kff以保证并网电流质量。Kff的取值范围为0～1，可以根据不同的需要根据实际情况灵活选取。当Kff取值为零时，即相当于未加入网压前馈环节。另外，从实验安全性角度上考虑，应最先选取网压瞬时值前馈Kff=1的条件进行并网实验。

图6为系统接入电网时，公共接入点的实际电压波形（空载），经示波器数据采样后，利用Matlab/Sinmulink将该电压作为公共接入点电压进行了分析和仿真。

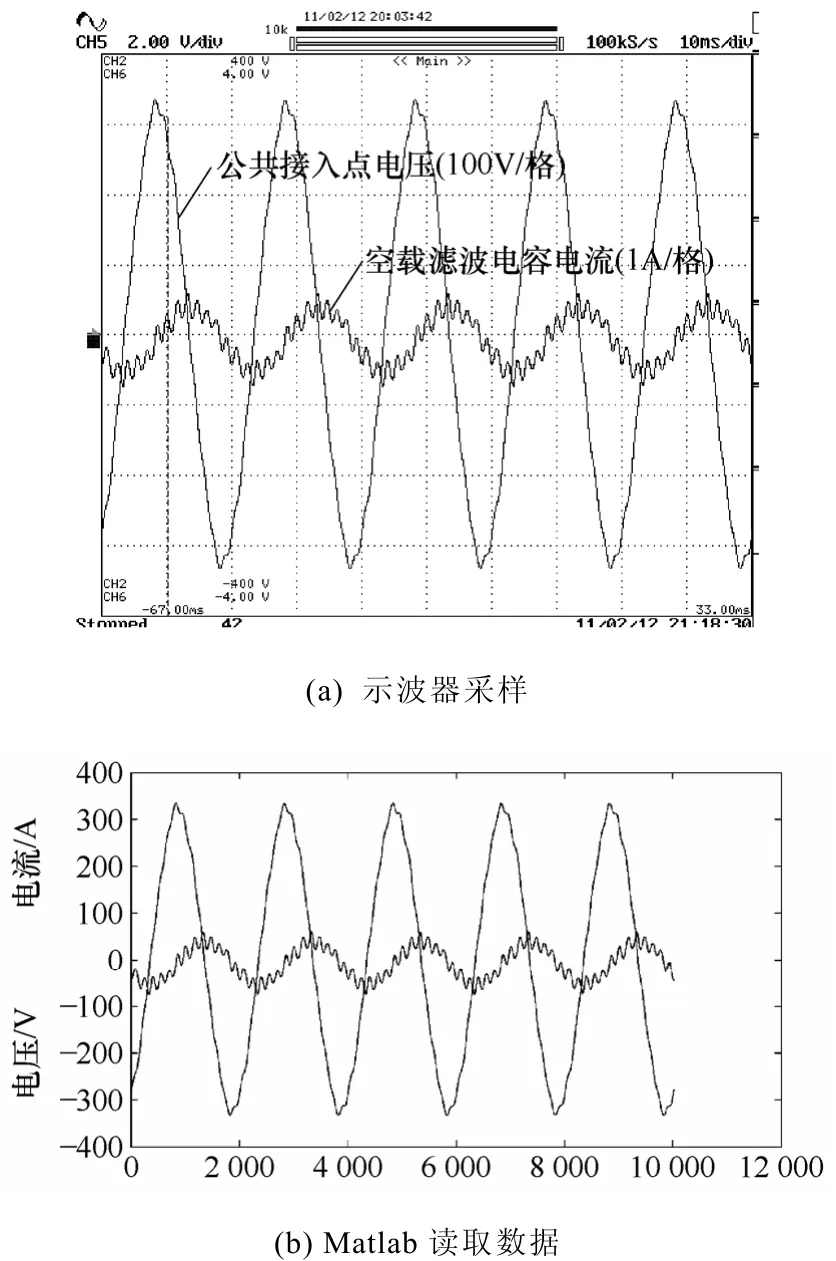
图6 公共接入点电压畸变Fig.6 PCC voltage distortion

图 7a中对采样电压进行了 FFT分析，可以看到，谐波主要集中在5次、7次、11次和13次。图7b是经过正序变换后的正序电压，可以看到，正序电压5次、13次谐波保持原有数值，其他次谐波的含量得到了降低。

接着，采用不同的前馈量进行并网电流控制仿真，结果如图8所示，可以看到，采用正序网压前馈的电流质量（THD=8.92%）优于采用网压瞬时值前馈的电流质量（THD=9.42%）。在图 8中可以看到，造成两者THD差异的主要原因在于11次电流谐波成分的不同，对于频率较低（5次、7次）的谐波，采样和计算的延时对瞬时值前馈的影响不大，瞬时值前馈可以较好的补偿网压，但是对于较高次谐波（11次），采样和计算延时导致了该频率下前馈量和实际量之间的误差加大，这时采用正序网压前馈的控制特性要优于网压瞬时值前馈。

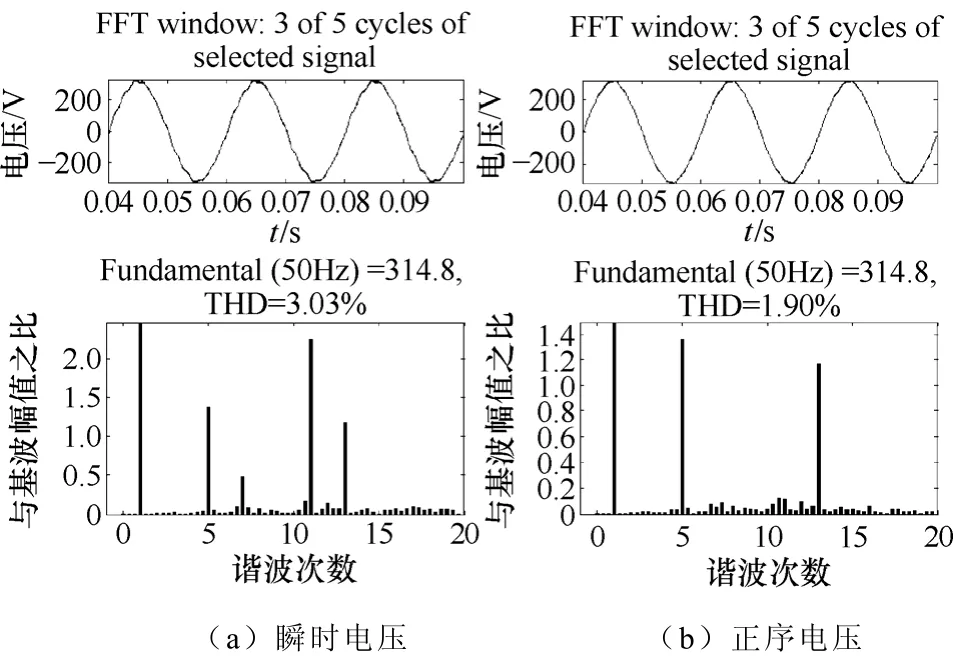
图7 公共接入点实测电压畸变FFT分析Fig.7 PCC voltage distortion FFT analysis

图8 逆变器侧仿真电流FFT分析Fig.8 Inverter side current FFT analysis

实际上，在系统实际工作中，采用不同前馈方式的电流质量区别更为明显，有关动态响应速度和实际电流质量的比较将通过实验证明。

5 实验验证

实验拓扑如图9所示。系统采用变流器内部整流桥作为直流电源，并通过前端调压器调整直流电压，经逆变器后，通过变压机柜并网。

实验变流器采用Danfoss FC 302 5.5kW通用变流器（其控制板及接口板已更换）。控制器采用dSPACE CP1103，光纤隔离驱动。需说明的是，在图9中1#设备即为并网变压机柜，内附带隔离变压器，除可以调压，调节并网阻抗外，还可模拟多种电网故障情况（用于电网故障穿越实验）。2#为滤波器及传感器部分，如图4所示。

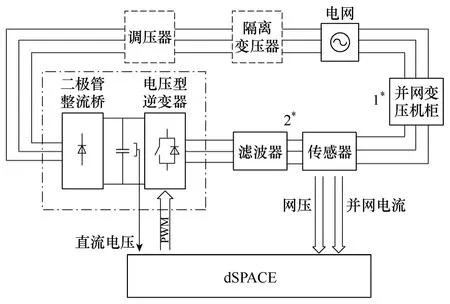
图9 实验拓扑Fig.9 Experimental topology

本实验平台旨在模拟“背靠背”永磁直驱风力发电系统的故障穿越特性，本文所涉及控制部分仅为电网侧并网控制部分。实验直流电压700V（逆变器并网工作时降至650V），电网相电压230V RMS，50Hz，并网电抗 5mH，实验功率 3kW。图 10～图12为示波器系统启动采样图，为了更清楚的区分电压、电流，在测量时并网电流方向取反。

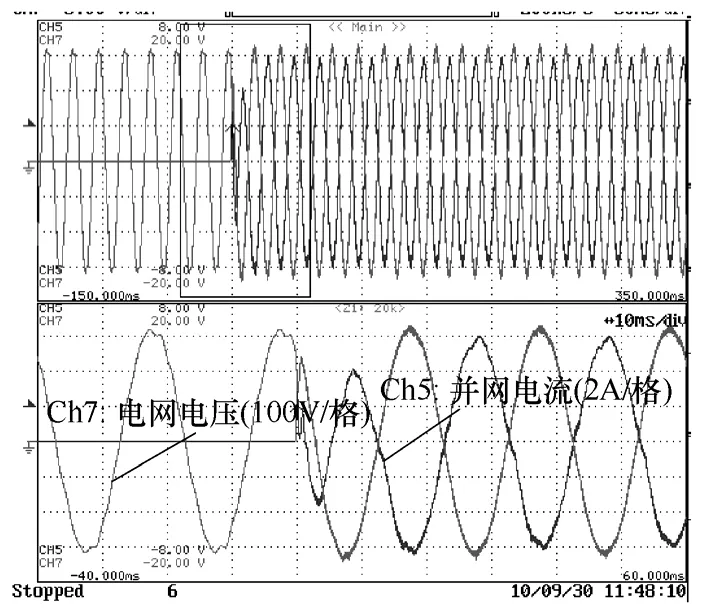
图10 无网压前馈Fig.10 Waveforms without voltage feed-forward

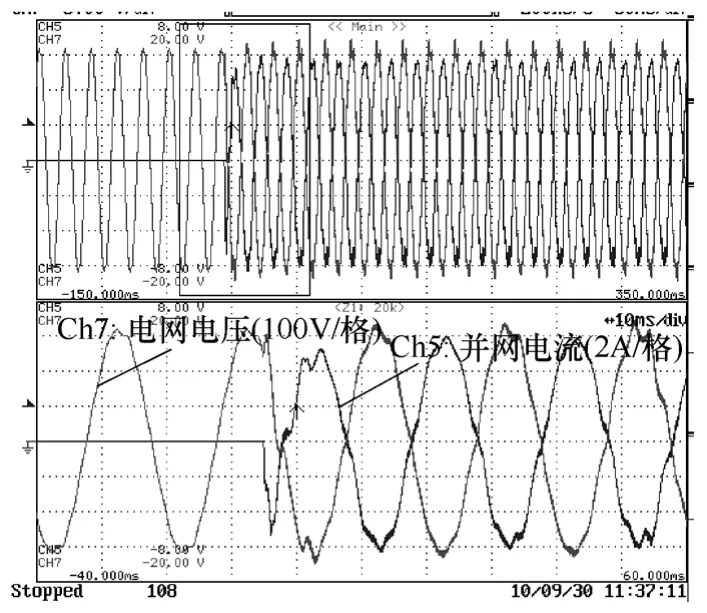
图11 网压瞬时值前馈（Kff = 0.9）Fig.11 Waveforms with grid voltage feed-forward

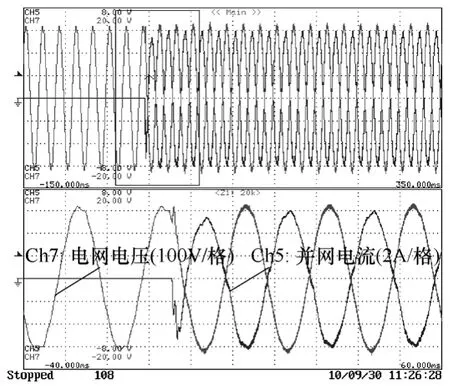
图12 正序网压前馈（Kff = 1）Fig.12 Waveforms with positive voltage feed-forward

从图 10～图 12中均可以看到，并网变流器工作前的变流器公用接入点电压已发生畸变，该畸变由实验所在电网环境中的大功率非线性负载中央空调与较大的并网电抗（见图4）共同导致。图10为未采用网压前馈控制的3kW实验波形，从该波形图上可以看到，其并网电流质量良好。图11为采用网压瞬时值前馈 3kW 实验波形，从该波形图可以看到，并网电流跟踪指令速度加快，但是并网电流无法得到良好控制，此处选择Kff=0.9的原因在于，当采用Kff=1，电流畸变过于严重，噪声大，为保证系统安全，选取 Kff=0.9，同时也说明当降低 Kff系数时，并网电流波形质量可以得到改善。由于并网电流无法得到良好的控制，当电流经过并网阻抗后，使得接入点电压同图 10相比畸变进一步加剧。图12为采用正序网压前馈的实验波形，在保证响应速度的同时，其并网电流质量也得到了保证。

图13是作者为进行此实验所设计的 dSPACE控制面板。图中显示了 3kW 网压正序前馈实验时dSPACE采集的数据，包括：直流电压（滤波前后）、网压、并网电流、输出调制波形、并网电流指令值输出功率（有功无功）、电流跟踪对比和网压正序分量。图中被框中的部分，即为前馈选择方式及Kff系数调节部分。图左下部分为死区补偿控制，采样直流偏移量清除及控制系数调节部分。从该图可以看到，在采用正序网压前馈时并网电流可以良好地跟踪电流指令值，实现无静态误差控制，同时可以取得理想的并网电流质量。

6 结论

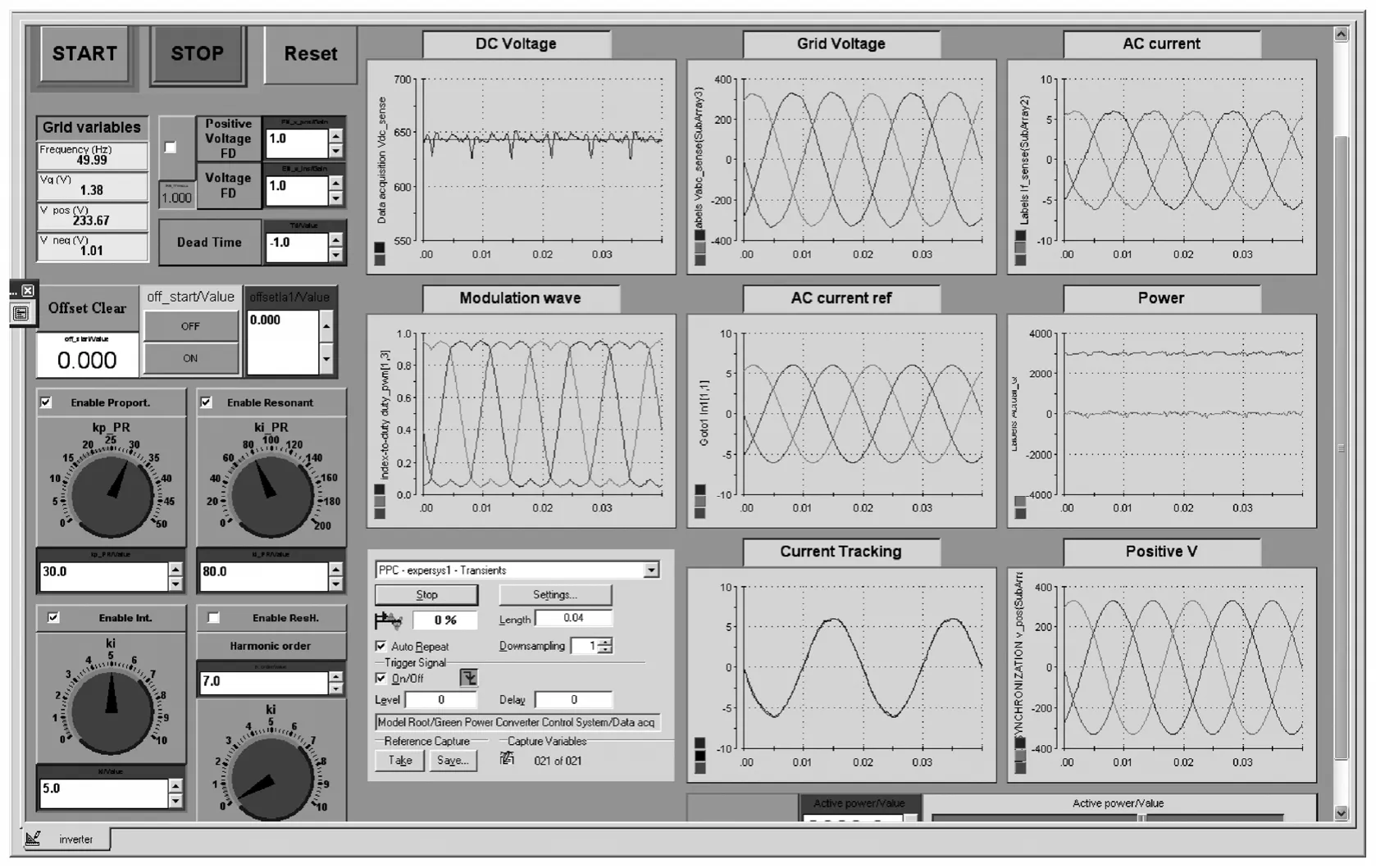
图13 dSAPCE控制面板3kW实验数据Fig.13 Experimental data from dSPACE control desk (3kW experiments)

针对近年来，在分布式发电系统中，对并网动态响应速度不断提高的要求，例如在风力发电并网时电网故障穿越的问题。在原有静止坐标系比例谐振控制的基础上，加入了带有比例系数的正序网压前馈环节。通过这种方式，降低了直接加入网压前馈所引入的电网干扰，同时相比不带有网压前馈的控制方法，提高了系统对于网压突变的响应速度。

通过研究表明：①采用比例谐振控制器跟踪静止坐标系下的正弦电流指令可以实现无静态误差控制；②采用网压前馈可以进一步提高静止坐标系控制对于网压突变的应变能力；③当采用网压瞬时值前馈时，会引入变流器公共接入点（PCC）电压畸变，由于采样等延时，引入的畸变电压特别是高次成分恶化并网电流质量，因此作者在本篇论文中使用正序网压前馈，对电网电压特定次谐波进行了滤波，在保证响应速度的同时，改善了并网电流质量；④同时考虑到在网络阻抗较大的情况下，正序网压内所含有的其他次谐波仍然会对并网电流造成影响，在前馈环节中加入了比例系数，可以平衡对动态性能和电流质量的要求。同时，本文通过实验证明了以上结论。

综上，静止坐标系下的比例谐振控制相比常用的同步旋转坐标系下的网压定向矢量控制具有对特定频率响应速度快，不存在耦合项，易实现谐波补偿这三个最显著的特点。相信在未来并网变流器控制器设计中，该种控制方法将会得到进一步的应用。

[1]周德佳, 赵争鸣, 袁立强, 等. 300kW光伏并网系统优化控制与稳定性分析[J]. 电工技术学报, 2008,23(11)∶ 116-122.Zhou Dejia, Zhao Zhengming, Yuan Liqiang, et al.Optimum control and tability stability analysis analysis for a 300kW photovoltaic gridgrid-connected connected system[J]. Transactions of China Electrotechnical Society, 2008, 23(11)∶ 116-122.

[2]Lin Ma, Xinmin Jin, Kerekes, et al. The PWM strategies of grid-connected distributed generation active NPC inverters[C]. Energy Conversion Congress and Exposition, 2009, 9∶ 920-927.

[3]Blaabjerg F, Teodorescu R, Liserre M, et al.Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5)∶1398-1409.

[4]马琳, 金新民, 唐芬, 等. 小功率单相并网逆变器并网电流的比例谐振控制[J]. 北京交通大学学报,2010, 34(2)∶ 118-133.Ma Lin, Jin Xinmin, Tang Fen, et al. Proportionalresonant gird-connected current control of low power single phase inverte[J]. Journal of Beijing Jiaotong University, 2010, 34(2)∶ 118-133.

[5]Teodorescu R, Blaabjerg F, Borup U, et al. A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation[C]. IEEE Applied Power Electronics Conference, and Exposition, 2004, 1∶ 580-586.

[6]陈炜, 陈成, 宋战锋, 等. 双馈风力发电系统双PWM 变换器比例谐振控制[J]. 中国电机工程学报,2009, 29(15)∶ 1-7.Chen Wei, Chen Cheng, Song Zhanfeng, et al.Proportional-resonant control for dual PWM converter in doubly fed wind generation system[J].Proceedings of the CSEE, 2009, 29(15)∶ 1-7.

[7]Bhowmik S, Spee R, Enslin J H R.Performance optimization for doubly fed wind power generation systems[J]. IEEE Transactions on Industry Applications, 1999, 35(4)∶ 949-958.

[8]Petersson A, Harnefors L, Thiringer T.Evaluation of current control methods for wind turbines using doubly-fed induction machines[J].IEEE Transactions on Power Electronics, 2005, 20(1)∶ 227-235.

[9]Teodorescu R, Blaabjerg F, Liserre M, et al.Proportional-resonant controllers and filters for grid-connected voltage-source converters[J]. IEE Proceedings of Electric Power Applications, 2006,153(5)∶ 750-762.

[10]Mattavelli P. A closed-loop selective harmonic compensation for active filters[J]. IEEE Transactions on Industrial Applications, 2001, 37(1)∶ 81-89.

[11]Zmood D N, Holmes D G.Stationary frame cruuent regulation of PWM inverters with zero steady-state error[J].IEEE Transactions on Power Electronics,2003, 18(3)∶ 814-822.

[12]Hasanzadeh A, Onar O C, Mokhtari H, et al. A proportional-resonant controller-based wireless control strategy with a reduced number of sensors for parallel-operated UPSs[J]. IEEE Transactions on Power Delivery, 2010, 25(1)∶ 468-478.

[13]Yuan X, Merk W, Stemmler H, et al. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions[J]. IEEE Transactions on Industrial Applications, 2002, 38(2)∶ 523-532.

[14]Shuitao Yang, Qin Lei, Peng F Z, et al. A robust control scheme for grid-connected voltage source inverters[C]. Applied Power Electronics Conference and Exposition, 2010 Twenty-Fifth Annual IEEE,2010∶ 1002-1009.

[15]Rodriguez P, Teodorescu R, Candela I, et al. New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions[C]. IEEE Power Electronics Specialists Conference, 2006, 37∶ 1-7.