微网用分布式电源变流器下垂特性控制策略

黄 杏 金新民

（北京交通大学电气工程学院 北京 100044）

1 引言

不同于传统电力系统“大机组，大电厂和大电网”的集中供电思想[1]，分布式电源规模小灵活性高，可以实现对负荷的就近安装，并直接应用于低压配电网[2]。分布式供电可对集中供电做出有力的补充：对于偏远地区用户，分布式电源的就近安装可以大大缩短输电距离，减小输电损失；而对于一些对供电质量要求较高的用户，分布式电源可以在电网故障或断电时，为其提供离网下的稳定供电，从而大大提高供电稳定性[3,4]。

作为分布式电源的重要组成部分和未来发展方向，必须使用电力电子装置作为输出功率变换单元的一次能源（如蓄电池、光伏、风力发电等）在微网用分布式电源中所占的比率越来越高。与传统的并网变流器控制策略相比，微网用分布式电源变流器的控制策略明显复杂：传统的并网变流器具有电流源的输出特性，只负责在电网正常的情况下，向电网提供功率；而微网用变流器不但要在并网状态下为电网提供功率，还要在离网状态下为微网内负荷提供稳定的电压和频率支撑，因此微网用分布式电源变流器应当具有电压源的输出特性。

微网用分布式电源在应用的过程中，经常需要多台电源并联运行，共同分担负荷，共同稳定微网系统电压和频率。为实现分布式电源无互联信号线情况下的并联稳定运行，诸多文献在微网用分布式电源变流器具有电压源输出特性的基础上，将传统电力系统中发电机的电压和频率下垂特性引入变流器的功率控制特性中[5-11]：文献[6]研究了单相电压源输出特性变流器的并联运行；文献[7]在一次调频基础上，向变流器控制策略中加入虚拟同步发电机的二次调频特性，但其控制的目标仅限于阻止系统频率偏离标准值。诸多文献[5-11]将研究重点放在了多台并联微网用变流器在并网状态和离网状态下的稳定运行控制，却忽略了变流器在两种状态之间的无缝切换（seamless transition）功能。这使得微网用变流器在并网状态和离网状态之间的切换过程中，可能出现停机再重启的问题，严重影响供电质量。

本文从微网用分布式电源变流器的工作原理出发，提出了一种新的基于下垂特性（有功功率-频率下垂特性和无功功率-电压下垂特性）的微网用分布式电源变流器控制策略，实现了多台并联运行的变流器从并网到离网状态的无缝切换。再通过引入基于平移下垂特性曲线的电网二次同步控制策略，使得变流器可以在无互联信号线并联的情况下，实现微网系统与电网的二次同步，完成微网系统离网状态到并网状态的无缝切换。本文通过仿真验证了这一控制策略的合理性，并在由多台三相25kW变流器组成的小型微网系统实验平台上进行了实验验证。

2 控制原理

2.1 变流器模型

图1为微网用分布式电源变流器的主电路图。由于分布式电源的一次能源种类繁多，为简化讨论，本文将一次能源等效为理想直流电压源，即任意时刻Vdc恒定不变。

为保证变流器在离网运行时，能够为微网内部负荷提供电能质量符合要求的交流电压，变流器利用变压器漏感组成LCL滤波电路，如图1所示。同时利用变压器实现电气隔离和三相四线制供电。

图1 微网用分布式电源变流器主电路图Fig.1 Microsource diagram

变流器的控制单元利用电压传感器和电流传感器，实时采集三相微网交流母线电压 Vabc(t)和变流器输出电流Iabc(t)。将微网交流母线电压Vabc(t)等效为电压V˙，变流器输出电流Iabc(t)等效为电流I˙。忽略谐波成分，将变流器半导体功率组件输出的三相PWM脉冲电压等效为电压E˙。在忽略滤波电容CF和线路杂散电阻的情况下，可以得到微网用分布式电源变流器的等效模型，如图2所示。

图2 微网用分布式电源变流器模型Fig.2 The microsource model

其中Xd的表达式为

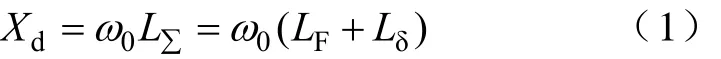
式中 ω0—微网交流母线电压基波角频率；

LF—交流滤波电感量；

Lδ—变压器等效漏抗。

在图2所示的变流器等效模型的基础上，可以得到变流器的相量图，如图3所示。

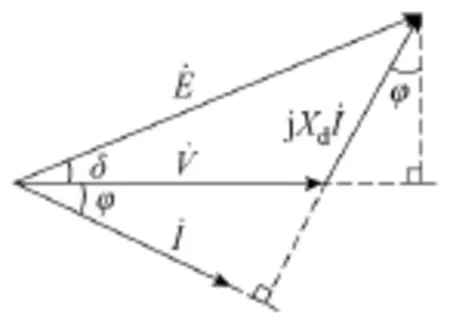
图3 微网用分布式电源变流器相量图Fig.3 Phase diagram for the microsource

根据图 3的变流器相量图，由文献[12]可知，微网用分布式电源变流器注入微网交流母线的有功功率PL和无功功率QL的表达式如式（2）和式（3）所示。

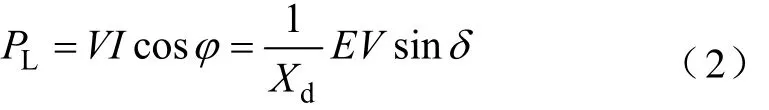
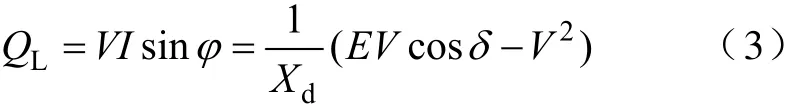
式中 φ —功率因数角；

δ —功角。

根据图 2中标注的参考方向可知，PL＞0表示变流器在向微网交流母线注入有功功率，反之为吸收有功功率；同理，QL＞0表示变流器在向微网交流母线注入感性无功，反之为容性无功。在功角δ足够小，以至于可以满足化简：sinδ≈δ，cosδ≈1时，式（2）和式（3）可以得到进一步化简，得到

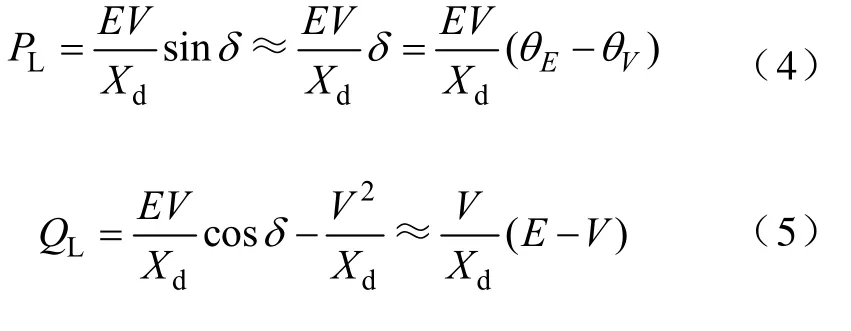
变流器可以实时检测微网交流母线电压V˙，并利用 PWM 脉冲控制半导体功率组件输出的电压E˙。因此，由式（4）可知，变流器输出的有功功率 PL正比于功角δ，通过调节电压E˙的相角θE，使之相对于V˙的相角差δ=θE-θV变化，变流器就可以实现对其输出有功功率PL的控制。同理，由式（5）可知，变流器输出的无功功率QL正比于两个电压的幅值差ΔV=E-V，因此变流器可以通过调节电压E˙相对于交流母线电压E˙的幅值差来控制变流器输出的无功功率QL。式（4）和式（5）是变流器同时实现电压源输出特性和多台并联同步运行的理论基础。

2.2 下垂特性曲线

传统电力系统中，发电机作为主力电源，其输出特性符合如图4所示的下垂特性曲线，即有功功率-频率下垂特性曲线和无功功率-电压下垂特性曲线。以有功功率-频率下垂特性曲线为例，假定系统中只有一台发电机向负荷供电，当系统因有功功率负荷增加而破坏了原有的有功功率平衡时，发电机的转速（频率）会因有功功率输出PL的增加而下降，当系统进入新的稳态时，系统的频率将低于初始值；反之，当系统有功功率负荷减小时，系统的频率将高于初始值。上述变化，即被称为“一次调频”。与之相类似，发电机无功功率-电压的静态特性被称为“一次调压”[12]。

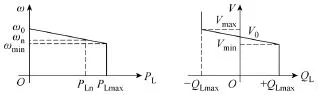
图4 下垂特性曲线：一次调频和一次调压Fig.4 Droop control characteristics： primary regulation

当系统的频率或电压偏离标称值过大时，系统可以通过平移发电机下垂特性曲线的方式，对系统的频率或电压进行二次调整，即“二次调频”或“二次调压”，如图5所示。同样以二次调频为例，假定系统中只有一台发电机向负荷供电，当系统频率偏离标称值过大（ωA）时，系统可以通过通信，向发电机发送指令，向下平移其有功功率-频率下垂特性曲线。假设调节过程中系统负荷不变，系统将进入新的稳态（ωB），从而实现了系统的频率调整功能。与二次调频相类似，系统对发电机无功功率-电压的静态特性的调整，被称为“二次调压”。

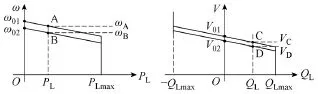
图5 下垂特性曲线：二次调频和二次调压Fig.5 Droop control characteristics： secondary regulation

当系统中有多台并联运行的发电机组时，以二次调频为例，其二次调整一般由其中的一台或少数几台发电机组，即主力调频机组承担；而系统中其他机组则只按照其静态特性参加一次调频[12]。系统中所有发电机输出的有功功率最终按照各自的功-频静态特性自动分配：假设系统负荷不变，当主力调频机组进行二次调频时，系统中其他发电机输出功率将因系统频率的变化而发生变化（根据其功-频静态特性）。主力调频机组为调整系统负荷，将对这部分功率变化量进行补偿，以保证频率调整过程中的有功功率平衡，因此被选为主力调频的机组必须拥有足够调整容量和调整范围。

在无互联信号线并联的情况下，为实现具有电压源输出特性的变流器多台并联稳定运行，诸多文献将上述传统电力系统发电机下垂特性引入微网用变流器的功率控制特性当中[7-12]。

利用图4所示的一次调频和一次调压，在并网状态下，由于系统电压的频率和幅值由电网决定且相对稳定，变流器可根据其输出端电压频率和幅值在下垂特性曲线中的位置，自动判断输出功率指令，从而运行于功率自动响应状态；在离网状态下，变流器可根据当前输出功率在下垂特性曲线中的位置，对系统电压的频率和幅值进行控制，从而为离网负荷提供满足下垂特性曲线的频率和电压支撑。

利用图5所示的二次调频和二次调压，并网时微网系统可以实现对变流器输出功率的主动调节；离网时，可以实现对系统电压和频率的主动调整，从而为系统离网到并网状态的无缝切换提供条件。

图4下垂特性曲线是实现变流器在无信号连接线情况下并联稳定运行的理论基础，同时为分布式电源变流器实现“即插即用”功能提供了条件。图5所示的下垂特性曲线二次调整是实现微网系统并网与离网状态之间无缝切换的理论基础。

3 变流器控制方法

当三相电压平衡时，变流器中同步旋转坐标系的q轴与三相合成电压矢量重合，d轴滞后q轴90°，且d轴分量为零。如图6所示。其中合成电压V˙为微网交流母线电压，E˙为变流器半导体功率组件输出电压。

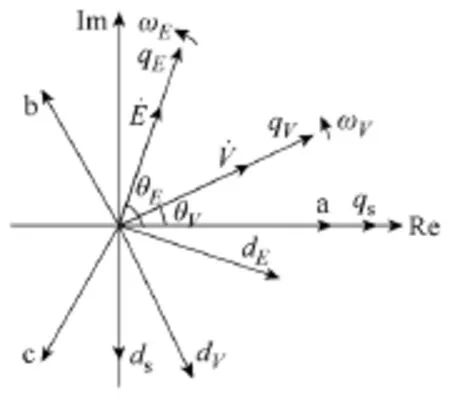
图6 微网用分布式电源变流器控制相量图Fig.6 Phase diagram of microsource

微网用变流器控制框图如图7所示。根据变压器的绕线方式，变流器将采集到的微网交流母线电压 VAB、VBC转化为变压器三角形侧三相电压 Va、Vb、Vc。锁相环 PLL利用Va、Vb、Vc计算得到其合成电压矢量V˙的频率fV和相角θV。为加强变流器对半导体功率组件的过电流保护能力，电流传感器与交流滤波电感 LF串联。在忽略滤波电容 CF中电流的情况下，检测电流 ia、ib即为变流器输出电流。功率计算单元利用同步旋转坐标系下变流器输出电流 id、iq和变流器输出端电压 Vd、Vq计算得到变流器输出功率PL，QL。

为实现变流器的电压源输出特性，保证离网情况下的稳定供电，变流器根据式（4）和式（5）直接控制半导体功率组件输出电压E˙：通过有功功率控制得到电压相量的相角θE；通过无功功率控制得到电压相量的幅值|E|。其中，当三相电压和三相负荷功率平衡时，电压E˙在同步旋转坐标系下满足Eq=|E|，Ed=0。

图7 微网用分布式电源变流器控制框图Fig.7 Control diagram of the microsource

3.1 有功功率-频率下垂特性控制

微网用分布式电源变流器有功功率-频率下垂特性的表达式为

式中 Pref—变流器输出有功功率给定值；

ω0—有功功率为零时母线电压角频率；

ωV—当前微网交流母线电压角频率；

m—曲线斜率，m=PLmax/（ωmin-ω0）。

由式（6）可知，利用一次调频，微网用变流器可以根据本地信息：变流器接入点微网交流母线电压角频率ωV，自动判断其输出有功功率Pref大小。

由式（4）可知，变流器输出的有功功率 PL正比于功角δ，变流器可以通过调节电压E˙的相角θE来间接控制功角δ，从而实现对变流器输出有功功率的控制，其控制方程为

式中 ΔP—变流器输出的有功功率偏差；

kf—比例控制系数。

3.2 无功功率-幅值下垂特性控制

微网用变流器无功功率-电压下垂特性的表达式为

式中 Qref—变流器输出无功功率给定值；

V0—无功功率为零时母线电压幅值；

Vq—当前微网交流母线电压幅值；

n—曲线斜率，n=QLmax/(Vmin-V0）。

由式（8）可知，利用一次调压，微网用变流器可以根据本地信息：变流器接入点微网交流母线电压的幅值Vq，自动判断其输出无功功率大小Qref。

由式（5）可知，变流器输出的无功功率QL正比于幅值差ΔV=E-V，因此变流器可以通过调节电压相量E˙的幅值E=ΔV+V来控制变流器输出的无功功率QL，其控制方程为

式中 ΔQ —变流器输出无功功率的偏差；

kVp—PI控制器比例系数；

kVi—PI控制器积分系数。

3.3 并离网无缝切换控制

微网交流母线与公共电网之间，通过一个受微网控制系统控制的公共连接点开关PCC-S0相连，如图8所示。为实现微网系统并网与离网状态之间的无缝切换功能，需微网控制系统对系统内多台并联的微网用变流器进行协调控制和能量调度。

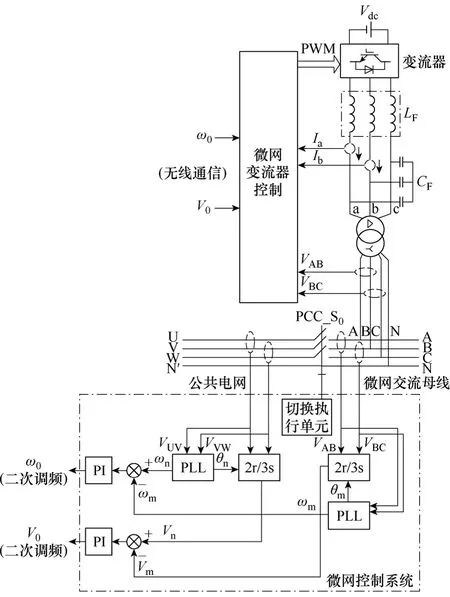
图8 微网系统换控制框图Fig.8 The diagram of the microgrid controller system

利用电压传感器，微网控制系统能够同时检测公共电网电压VUV、VVW和微网交流母线电压VAB、VBC，并通过锁相环 PLL计算得到公共电网电压的角频率ωn、相角θn以及微网交流母线电压的角频率ωm和相角θm。最终计算得到公共电网电压nV˙和微网交流母线电压mV˙。

当微网控制系统检测到公共电网故障：电网失电、电网欠电压等故障时，将控制公共连接点开关PCC-S0断开，完成微网系统从并网状态到离网状态的切换。切换过程中，由于微网用变流器具有电压源的输出特性，能够为微网系统内部负荷提供稳定的频率和电压支撑。因此，在容量允许的范围内，微网用变流器能够支持微网系统实现并网状态到离网状态的无缝切换，并在离网状态下通过一次调频和一次调压进行自动的负荷分配，保证多台并联稳定运行。

当微网控制系统检测到电网故障恢复时，微网系统需要重新并网运行。此时，为实现离网到并网状态的无缝切换，抑制在PCC-S0闭合过程中产生的冲击电流，在闭合开关之前，微网交流母线电压必须先实现与公共电网电压的二次同步，即实现两者同频同相同幅。为实现上述功能，微网控制系统需使用通信对微网变流器进行二次调压和二次调频控制，如图8所示。

微网控制系统对微网变流器的二次调压和二次调频控制分别通过对变流器下垂特性曲线中的空载频率ω0和空载电压V0的控制调节完成，如图5所示。假定系统中只有一台变流器向负荷供电，以二次调频为例，离网系统运行于A点，此时空载频率为ω01，微网系统电压频率ωA大于电网频率。为完成离网到并网状态的无缝切换，二次并网前，微网系统频率应等于电网频率，因此微网控制系统利用PI闭环控制，对变流器进行二次调频控制，将空载频率调整为ω02。假设微网系统有功负荷 PL不变，则当进入新的稳态（ωB）时，微网系统频率将调整为与电网频率相同。微网控制系统对微网变流器的二次调压控制，与上述二次调频控制过程类似。

当系统中有多台微网用分布式电源变流器时，系统可以从中选出一部分拥有足够调整容量和调整范围的变流器，作为主力调压或调频电源，具有下垂特性二次调整的功能，而其他变流器则保有下垂特性一次调整功能即可。当微网系统需要对系统进行电压或频率调整时，微网系统可通过对少数主力调压或调频电源的控制，来实现对微网系统电压或频率的调整，从而大大化简系统的控制。

微网控制系统在对微网内变流器进行上述二次调压和二次调频控制的同时，还在对微网系统电压与电网电压的同步状态进行实时判断：①微网系统电压频率已进入新的稳态，且与电网频率相同；②微网系统电压幅值已经入新的稳态，且与电网电压幅值相同；③微网系统电压相位与电网电压相位相同。当微网系统电压同时满足上述三个条件，即与电网电压同频率同相位同幅值时，微网控制系统将控制公共连接点开关PCC-S0重新闭合，完成微网系统从离网状态到并网状态的切换。由于在开关闭合前，微网系统电压与电网电压同步，开关两端电压差为零，因此在离网状态到并网状态的切换过程中，公共连接点处不会产生过大的冲击电流，从而使得微网系统能够完成离网到并网状态的无缝切换。

4 仿真

为验证本文所提出的控制策略而搭建的微网系统实验平台如图9a所示，实验台包含四台变流器、一组负荷以及一个微网控制系统，其中四台变流器额定容量相同（25kVA），负荷为有功功率无功功率可调负载。本文利用该微网系统实验平台中的两台电源（变流器1和变流器2）以及负荷，组建小型微网系统，对微网用变流器的控制策略进行了实验验证，并利用Matlab仿真软件，对该实验系统进行了仿真建模，如图9b所示。

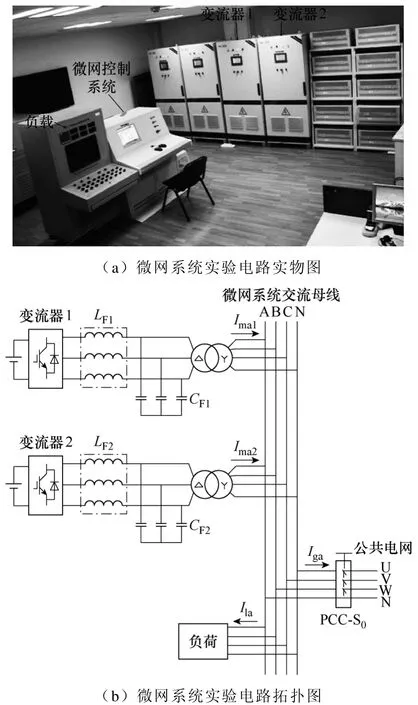
图9 微网系统实验电路Fig.9 Test circuit of microgrid system

两台变流器的下垂特性曲线如图5所示，其中空载频率 f01=51Hz，f02=50.5Hz，PLmax=20kW，V01=311V，V02=305V，QLmax=15kvar，额定电压下，微网系统内部负荷 PL=25kW，QL=15kvar。系统在0.4s时断开公共连接点开关PCC-S0，使微网系统从并网状态转换到离网状态。

并网运行时，由于电网电压的合成电压频率为50Hz，幅值为311V，因此稳态时变流器1输出功率PL1=10kW，QL1=0；变流器2输出功率PL2=5kW，QL2= -2.9kvar；微网系统交流母线向电网提供功率PPCC=PL1+PL2-PL= -10kW，QPCC=QL1+QL2-QL=-17.9kvar，即并网时公共电网与变流器1和变流器2共同分担微网系统内部负荷。由此可知，当微网系统进入离网运行状态后，因失去公共电网的供电功率，微网系统交流母线电压的频率fm和幅值Vm将因变流器1和变流器2输出功率的增加而减小，如图10a和图10b所示。两台变流器输出功率会在微网系统离网后重新分配，微网系统进入新的稳态，如图10c和图10d所示。以上的仿真结果表明，本文提出的控制方法能够实现微网用分布式电源变流器并联情况的并网和离网状态的稳定运行。

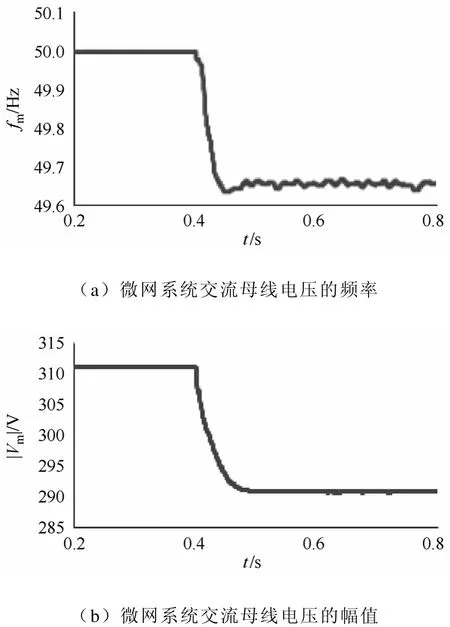
图10 微网系统并网到离网仿真波形Fig.10 Waveforms during the islanding

5 实验

为进一步验证本文所提出的控制策略的可行性，还搭建了由两台微网用变流器和一个负荷组成的微网实验系统，如图9a所示。两台变流器的下垂特性曲线相同，如图4所示，其中空载频率f01=51Hz，PLmax=20kW，V01=311V，QLmax=15kvar。

图11为微网系统从并网状态到离网状态切换过程中的电压电流波形，箭头所指为离网时刻。从波形可以看出，系统实现了并网状态到离网状态的不停机切换。离网后，两台微网电源只需向微网负荷提供功率，而无需再向电网提供功率，因此离网切换后，两台微网电源输出功率突然减小，且由于两台微网电源下垂特性曲线相同，两台变流器输出功率相等，离网后各分担微网负荷的一半。

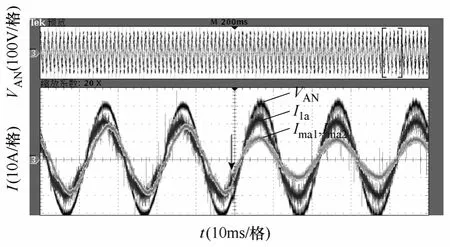
图11 并网到离网切换时刻的电压电流波形Fig.11 Waveforms during islanding

图12为微网系统从离网状态重新并网时的波形，箭头所指为并网时刻。从波形可以看出，系统实现了重新并网过程中的不停机切换。

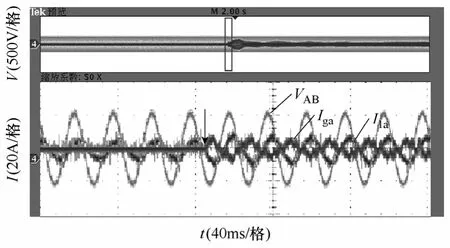
图12 重新并网时电压电流波形Fig.12 Waveforms during resynchronization

6 结论

本文提出了一种微网用分布式电源变流器控制方法，使得微网用变流器具有电压源的输出特性，而非传统并网变流器的电流源输出特性。这种电压源的输出特性使得变流器能够在离网运行时，为微网负荷提供稳定的电压和频率支撑，并完成并网状态到离网状态的不停机切换。再通过引入传统发电机的下垂特性曲线，使得微网用变流器在电压源输出特性的基础上，具有无互联信号线并联下的负荷自动分配功能，从而有利于实现变流器“即插即用”功能。最后，提出通过二次调压和二次调频的方式，实现微网用变流器对微网系统电压频率和幅值的主动调节功能，从而实现了微网用变流器从离网状态到并网状态的不停机切换。仿真和实验结果都验证了本文所提出的控制方法的合理性和有效性。

[1]鲁宗相, 王彩霞, 闵勇, 等. 微电网研究综述[J].电力系统自动化, 2007, 31(19)∶ 100-107.Lu Zongxiang, Wang Caixia, Min Yong, et al.Overview on microgrid research[J]. Automation of Electric Power System, 2007, 31(19)∶ 100-107.

[2]王成山, 王守相. 分布式发电供能系统若干问题研究[J]. 电力系统自动化, 2008, 32(20)∶ 1-4.Wang Chengshan, Wang Shouxiang. Study on some key problems related on distributed generation systems[J]. Automation of Electric Power System,2008, 32(20)∶ 1-4.

[3]Lasseter R H, Piagi P. Microgrid∶ a conceptual solution[C]. IEEE Power Electronics Specialists Conference, 2004, 6∶ 4285-4290.

[4]Abu-Sharkh S, Arnold R J, Kohler J, et al. Can microgrids make a major contribution to UK energy supply[J]. Renewable and Sustainable Energy Reviews,2006, 10∶78-127

[5]姜桂宾, 裴云庆, 杨旭, 等. SPWM逆变电源的无互联信号线并联控制技术[J]. 中国电机工程学报,2003, 23(12)∶ 94-98.Jiang Guibin, Pei Yunqing, Yang Xu, et al. Parallel operation of sinusoid wave inverters without control interconnections[J]. Proceedings of the CSEE, 2003,23(12)∶ 94-98.

[6]朱丹, 苏建徽, 吴蓓蓓. 基于虚拟同步发电机的微电网控制方法研究[J]. 电力系统及其自动化, 2010,32(4)∶ 59-62.Zhu Dan, Su Jianhui, Wu Beibei. Research on control methods of microgrid based on virtual synchronous generators[J]. Power System & Automation, 2010,32(4)∶ 59-62.

[7]王成山, 肖朝霞, 王守相. 微网中分布式电源逆变器的多环反馈控制策略[J]. 电工技术学报, 2009,24(2)∶ 100-107.Wang Chengshan, Xiao Zhaoxia, Wang Shouxiang.Multiple feedback loop control scheme for inverters of the micro source in microgrids[J]. Transactions of China Electrotechnical Society, 2009, 24(2)∶ 100-107.

[8]Lee C T, Chu C C, Cheng P T. A new droop control method for the autonomous operation of distributed energy resource interface converters[C]. Energy Conversion Congress and Exposition, 2010.

[9]Goya T, Omine E, Senjyu T, Yona A, et al. Frequency control in isolated island by using parallel operated battery systems applying H∞control theory based on droop characteristics[J]. The Institution of Engineering and Technology, 2011, 5(2)∶ 160-166.

[10]Liao H, Wu C S. A voltage stability droop control strategy of wireless parallel inverters[C]. International Conference on Electrical and Control Engineering,2010.

[11]Ritwik Majumder, Gerard Ledwich, Arindam Ghosh,et al. Droop control of converter-interfaced microsources in rural distributed generation[J]. IEEE Transactions on Power Delivery, 2010, 25(4)∶ 2768-2778.

[12]何仰赞, 温增银. 电力系统分析[M]. 武汉∶ 华中科技大学出版社, 2003.