气候多变型区域配电系统可靠性预测
2012-07-02孙京锋周步祥王学友
孙京锋,周步祥,林 楠,徐 飞,林 波,王学友
(1.四川大学电气信息学院,成都610065;2.四川电力职业技术学院,成都610071)
配电系统的可靠性是整个电力系统结构及运行特性的集中反映,而恶劣天气条件下元件发生故障的可能性将大大增加。由于电力系统输配电线路特别是长距离高压输电线路长期处在复杂的天气环境中,其故障的发生受天气变化的影响很大。因此,系统的原始参数如故障率、维修率等是其所处天气状态的函数[1]。
以往的可靠性算法中,多针对单一气候状态或双气候状态的可靠性计算,而对恶劣天气情况下配电网系统的可靠性计算却少有涉及。配电系统的故障往往受多种因素的影响,这些因素本身具有内在的相关性,如台风来临时伴随的强风、暴雨,寒潮来临时伴随的强降雪、冰雹等,综合考虑这些因素的相互作用将使故障的"凝聚效应"更加明显。在气候多变区,特别是在恶劣天气条件下元件发生故障的概率将明显增大,由此可能造成配电网发生故障的可能性也随之增大,严重的可能造成例如大面积停电类似的重大事故。因此,在天气多变区域配电网可靠性评估中考虑气候变化对可靠性的影响是十分必要的[2,3]。
根据气候变化具有随机性的特点,将三态气象条件下的配电网故障分类,并由于配电系统本身结构和运行环境的复杂性,系统运行过程中所检测到的特性参数(即观测序列)并不能与状态简单的一一对应。而隐马尔科夫链模型含一种双重随机过程机制,可以将观测序列与隐状态通过一组概率分布联系起来,从而可以更加真实地描述系统实际运行情况[4]。因此,本文引入HMC模型分析配电系统运行可靠性,通过监测的多观测序列来识别系统运行过程中隐含的状态变迁过程,由系统状态变迁过程来推断其运行可靠性。
1 考虑天气影响的隐马尔科夫链模型
1.1 天气状态的等效
气候具有随即变化的特点,为便于分析计算,需将其处理为一个状态足够少又可完全描述故障“聚集效应”的状态函数,基于此,利用IEEE346[5]标准中对气候的分类将天气状态分为三类:正常天气、恶劣天气、灾难天气。其中,正常气候对元件故障率影响最小。
天气的变化是一个可以处理为三种天气情况的随机过程,图1表示在一个统计周期T内天气随即变化的情况。

图1 天气随机变化图Fig.1 Diagram of the random weather distribution
图中λ″表示灾难天气时元件故障率的期望值,λ′表示恶劣天气时元件故障率的期望值,λ表示正常天气时元件故障率的期望值,dt表示灾难天气的持续时间,st表示恶劣天气的持续时间,nt表示正常天气的持续时间。

图2 一个统计周期内天气持续时间的期望值Fig.2 Expected value of weather duration time in a cycle
1.2 隐马尔科夫链模型
马尔科夫理论认为,世界上无论自然领域还是社会领域,有一类事物的变化只与近期状态有关,与事物的过去状态无关,事物的这种性质称为无后效性[6]。配电网的供电可靠性正满足马尔科夫理论所描述的这一类事物的特点。
HMC模型[7,8]是一种状态隐含、观测序列可见的双重随机过程,从而可以将观测序列与隐状态通过一组状态分布联系起来。包括具有状态转移概率的马尔科夫链隐式随机过程和与马尔科夫链每个状态相关联的观测序列的显式随机过程。
如图1所示,HMC模型一般被表示为一个五元组:

其中,N表示状态,记N个状态出现的概率分别为θ1,θ2,…,θN,则马尔科夫链所处的状态概率行向量为qi,qi= (θ1,θ2,…,θN);M表示每种状态对应的可能的故障率,记M个可能的故障率为V1,V2,…,VN,则元件的状态故障率向量为ot,ot= (V1,V2,…,VM)T;A表 示 状 态 转 移 概 率 矩 阵,A=|aij|N×N,aij=p(q(t+1)=θj|qt=θi)表示 从状态i转移到状态j的概率;B表示故障率概率矩阵,概率矩阵B=|bjk|N×M,bjk=P(ot=vk|qt=θj),表示天气情况为状态θi出现故障的概率;π表示状态分布向量,π= (π1,π2,…,πN)。
由于ai、bi和πi都表示概率,故它们满足以下条件:
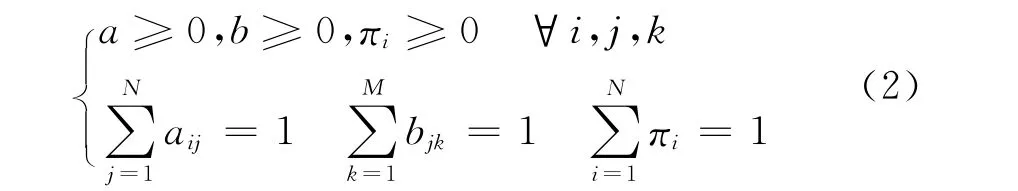
由此可见,HMC模型通过A、B和π的不同分布来描述双重随机过程。HMC的状态是不确定的,只能通过统计学得到状态的存在概率及其特性。HMC模型不仅考虑到各个状态之间的相关性,而且也考虑到观测序列在相应状态下存在条件独立性。
将HMC模型应用于实际工程时,通常采用Forward-Backward算法来解决模型的概率计算问题,即给定观测序列o= {o1,o2,…,oT}和模型λ,有效地计算在o给定λ下的概率;采用Viterbi算法解决模型的最优状态序列求解问题,即给定o={o1,o2,…,oT}\和λ,选择一个在某种意义上最优的状态序列Q= {q1,q2,…,qt};采用Baum-Welch算法解决模型的参数估计问题,即给定o={o1,o2,…,oT}和初始条件λ0,调整 HMC模型参数,使p(o|λ)最大。
2 基于HMC的区域配电系统可靠性预测
2.1 多态天气条件下元件的故障率
元件在不同天气条件下的故障率为一年内故障发生的次数,但是灾难天气在一年中所占的时间较短且具有随机性的特点(即灾难天气在哪一年出现或者在一年中出现的次数都是不确定的),因此,引入平均故障率λ^:

通常,N≫S≫D,故λ^≈λ。
实际中,λ、λ′和λ″的值很难得到,只能通过统计得到λ^的值,若知道故障发生在灾难性天气的百分比p1故障发生在恶劣天气的百分比p2则可由公式(4)得到:

通过对p1和p2的不同取值对λ、λ′和λ″的计算结果可知,元件在灾难天气条件下的故障率远大于在恶劣天气条件下的故障率、在正常天气条件下的故障率和平均故障率。
2.2 状态转移矩阵的确定
元件发生故障的过程可能伴随着天气状态的变迁,比如元件从正常运行开始,经过状态转移可能达到恶劣天气下的故障或者灾难天气下的故障发生。
初始条件下,若天气状态处于正常天气状态,则初始状态的概率分布向量为π=(1,0,…,0),状态变迁矩阵为A0和元件故障率矩阵B0采取随机或者均匀方法选取,从而得到初始条件下元件的HMC模型A = (A0,B0,π0)。
将性能特性参数在t时刻的多观测序列O=(o1,o2,…,ot)输入到初始 HMC模型λ0= (A0,B0,π0)中,利用Baum-Welch算法,经过迭代计算,得到元件在t时刻的DHMC模型 ,一般取迭代次数为10次。为了验证该HMC模型的合理性,采用Forward-Backward算法计算多观测序列O在给定λ下的概率,即P(o|λ)。如果P(o|λ)超过期望值0.8,则认为得到的 HMC模型λ= (A,B,π)是准确的。
2.3 可靠性指标的评估方法
线路可靠率根据元件自身可靠率以及元件间的串并联关系求取[9~12]。通常情况下已知线路s上n个元件各元件的故障率λfsi或可靠率λsi:

令Pi(t)表示系统在t时刻处于i天气状态下的概率。根据切普曼 -柯尔莫格洛夫微分方程有:

其中,P(t)= (P0(t),P1(t),…,Pn-1(t))为元件故障概率向量,P′(t)为P(t)的一阶微分状态向量。对式(6)进行Laplace变换,得:

若系统在初始条件下处于正常天气状态,则有:

同时,将t时刻状态变迁矩阵A带入式(6)中,可以得到:

接着,对P(s)进行Laplace逆变换,得到元件i在t时刻处于不同状态的概率:

从而,可以得到在t时刻元件的可靠率λsi:

线路可靠率根据元件自身可靠率以及元件间的串并联关系求取。对于上n个元件组成的串联系统,其线路可靠率为

对于n个元件组成的并联系统,其可靠率为:

对于线路s,假设系统的故障情况有N种,则系统的故障率指标:

3 仿真结果及算例分析
考虑附图3所示系统,该系统即可作为由两条线路组成的并联系统,也可以作为考虑二次故障的系统仿真结构图。若考虑天气状态对可靠性指标的影响,则系统出现故障的情况可能有三种:
a.元件1故障发生在正常天气;
b.元件1故障发生在恶劣天气;
c.元件1故障发生在灾难天气。
假定两条线路元件可靠性参数相同,即λ=0.3次/年,λ′=50.0次/年,λ″=0.09次/年,r1=8h,r2=8h,r3=2h,并且多太天气条件下期望持续时间为N=150h,S=1h,D=0.2h。

图3 并联线路示意图Fig.3 Simple system with two lines in parallel
若不计p1和p2的影响,利用式(3)可算出线路的平均故障率λ=0.629次/年。表1给出了系统在不同天气状态下可靠性参数的计算结果。情况A只考虑一种天气状态,情况B为系统在考虑3种不同天气状态下的可靠性参数值。
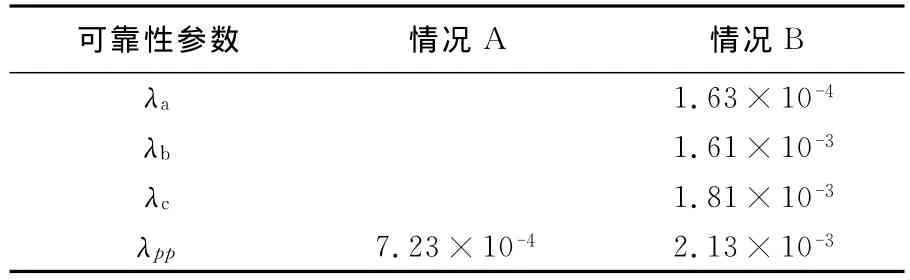
表1 系统在不同条件下的可靠性参数Tab.1 Reliability parameters of the system in various conditions
由表1可以看出情况A的λpp比情况B的λpp小的多,因为这种情况天气状态对系统故障率的影响,灾难性天气、恶劣天气中元件发生故障的概率比正常天气状态下元件故障的概率高的多。
若设元件故障发生在非正常天气的期望概率为P,则:

图4为故障率λ与期望概率P的关系曲线。

图4 可靠性指标与P值的关系曲线Fig.4 Curves of reliability index with parameter P
4 结语
本文在研究了天气状态对电力系统可靠性参数的影响情况下,建立了隐马尔科夫链模型,并进行了相应的可靠性参数计算。将天气状态引入电力系统可靠性评估中,使可靠性指标运算结果更具有实用性、现实性,因此考虑天气变化的影响能对可靠性评估、工程建造和电力系统运行维护产生积极的影响。
[1] Billiton R.Reliability Evaluation of Power Systems[M].London:Pitman Advanced Publishing Program,1984.
[2] Dichirico C,Singh C.Reliability analysis of transmission lines with common mode failures when repair times are arbitrarily distributed[J].IEEE Trans on Power Systems,1988,3(3):1012-1019.
[3] Billiton R,Wang P.Reliability-network-equivalent approach to distribution-system-reliability evaluation[J].IEE Proceedings-Generation,Transmission and Distribution,1998,145(2):149-153.
[4] Pisarn C,Theeramunkong T.An HMM-Based method for Thai spelling speech recognition[J].Computers and Mathematics with Applications,2007,54(1):76-95.
[5] IEEE Standard 346-1973,Terms for reporting and analyzing outages of electrical transmission and distribution facilities and interruptions to customer service[S].
[6] 马海云,张忠林(Ma Haiyun,Zhang Zhonglin).马尔可夫链模型在软件可靠性测试中的应用(Application of Markov chain model for software reliability testing)[J].中国测试技术(China Measurement Technology),2006,32(6):121-123.
[7] 胡英奇,刘建庸.马尔可夫决策过程引论[M].西安:西安电子科技大学出版社,2000.
[8] 龚光鲁,钱敏平.应用随机过程教程及其在算法与智能计算中的应用[M].北京:清华大学出版社,2003.
[9] 李晓辉,徐晶,李达,等(Li Xiaohui,Xu Jing,Li Da,et al).基于层次分析的配电网可靠性评估指标体系(Index system of reliability evaluation for distribution network based on analytic hierarchy process)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(3):69-74.
[10] 王成山,罗凤章,肖峻,等(Wang Chengshan,Luo Fengzhang,Xiao Jun,et al).基于主变互联关系的配电系统供电能力计算方法(An evaluation method for power supply capability of distribution system based on analyzing interconnections of main transformers)[J].中国电机工程学报(Proceedings of the CSEE),2009,29(13):86-91.
[11] 管霖,冯垚,刘莎,等(Guan Lin,Feng Yao,Liu Sha,et al).大规模配电网可靠性指标的近似估测算法(Approximate evaluation algorithm for reliability indices of cosmically distribution system)[J].中国电机工程学报(Proceedings of the CSEE),2006,26(10):92-98.
[12] 姚李孝,赵兵,伍利,等(Yao Lixiao,Zhao Bing,Wu Li,et al).基于混合算法的复杂配电系统可靠性评估(Hybrid method for the reliability evaluation of complex power distribution system)[J].电力系统及其 自 动 化 学 报 (Proceedings of the CSU-EPSA),2006,18(6):96-102.
