电网黑启动过程中的铁磁谐振分析
2012-07-02闫贻鹏林济铿
刘 涛,闫贻鹏,林济铿
(1.天津市电力公司技术中心,天津300384;
2.天津大学智能电网教育部重点实验室,天津300072)
在电网的黑启动过程中,可能发生铁磁谐振。其过程是在合线路与母线相连的断路器时,由于电感和对地电容的存在,会产生暂态冲击电流,对于母线处安装的电压互感器PT(potential transformer),冲击电流可能会使PT铁芯进入饱和区,从而与母线对地电容及线路分散电容间产生具有正反馈作用的充放电,而推高系统过电压和PT中的过电流。该现象的发生可能使得系统中弱绝缘设备发生对地闪络和PT的高压熔丝熔断,甚至烧毁PT[1~5]。因此,为了黑启动过程的设备安全及黑启动过程能够顺利完成,需密切关注该问题对于黑启动路径的影响。
数十年来,国内外的专家学者对铁磁谐振进行了大量深入研究,从各个不同角度解释了PT铁磁谐振的现象及其变化规律,给出了一些判据以及相应的分析方法,如物理模拟法[6,7]、图解法[8]、解析法[9,10]、微 分 方 程 数 值 解 法[11,12]、数 字 仿 真 分 析法[13,14]、小波分析法[15]等。
物理模拟方法利用物理模型来仿真实际的铁磁谐振现象,不改变原系统物理量的性质,只是物理量大小不同,因此它们之间有相同(或相似)的物理过程,但受设备的限制,其研究规模一般不大。图解法是利用铁芯线圈的U-I特性曲线及电路运行的伏安特性曲线在同一直角坐标系下进行分析,但其基础是建立在电路中各部分电流和电压都是工频或同一频率,对其他频率的谐振则没有考虑。解析法利用方程式代替电路的伏安特性和铁芯线圈的U-I特性,通过方程组联立求解,给出是否发生铁磁谐振的判据,但也只是工频铁磁谐振的判据。微分方程数值解法通过电路的微分方程与铁芯线圈的U-I特性方程,联立求解微分方程组,给出是否发生铁磁谐振的判据;该方法较为精确,考虑了全部频率,但求解过程相对复杂。小波分析法是利用一系列的滤波器对信号进行滤波,并对每一个尺度的小波分解,提取一个频段的信号分量,根据能量最大的频段判断谐振的类型;该方法由于需进行滤波和信号提取等操作,过程相对较为复杂。
应该说,上述方法均是讨论电路是否会发生铁磁谐振的判据或建模仿真,并没有对电路发生铁磁谐振的基本机理进行讨论。迄今并没有一个很统一的铁磁谐振的定义。本文首先讨论了铁磁谐振的物理本质是电容与非线性电感之间的充放电,并因非线性电感的进一步减小使得过电压及过电流相对于固定的电感电容充放电所导致的过电压及过电流更为严重。进而给出了基于铁芯线圈L-IL(IL为铁芯励磁电流有效值)特性方程的铁磁谐振仿真方法,并结合天津电网黑启动路径验证了铁磁谐振的本质问题,及相应预防措施。
1 铁磁谐振的物理本质
在黑启动过程中,闭合与母线相连的断路器,其电路可以等效如图1所示。其中R、L1为线路等效电阻和电感,C为母线的对地电容,L(IL)为PT中电感。为PT两端电压向量,即母线2电压向量,为线路两端电压向量,为电源电压向量,分别为PT中电流向量和母线对地电容中电流向量为线路中电流向量。
图1电路的工作点示意如图2所示,其横轴为PT中电流的有效值IL,纵轴为电压的有效值U。其中电源电压有效值E不随IL变化,在U-IL平面上为一条平行于IL轴的直线;从图1中可看出线路两端电压受电感电流与电容电流之和影响,所以线路两端电压向量为

图1 合闸时的等效电路Fig.1 Equivalent circuit for switch on
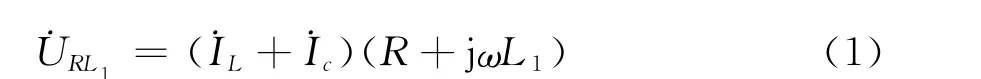
其中对地电容电流向量˙IC为

式中 ,˙Uc、˙UL分别为母线 对 地 电 容 和 PT 两端的电压向量,则式(1)可化成:
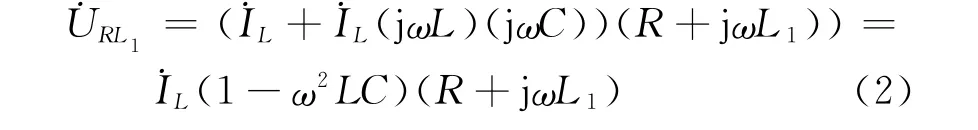
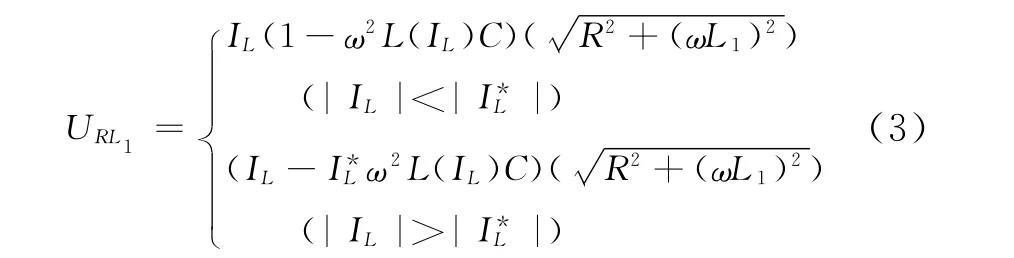
式(3)即为线路的伏安特性,可用图2中斜虚线表示;将电源电压与线路的伏安特性曲线合并,可得图2中所示的斜实线,该斜实线与PT的伏安特性曲线共有三个交点A、B、C,其中B、C点在第一象限,A点在第三象限。
当电路工作在A点或C点时,PT处于非线性区,此时会发生铁磁谐振现象,即对地电容与PT之间的正反馈充放电现象。其具体过程如下。
当PT运行在饱和区时,即图2中的A点或者C点,PT中的电感值L(IL)减小。PT与电容并联支路的阻抗为
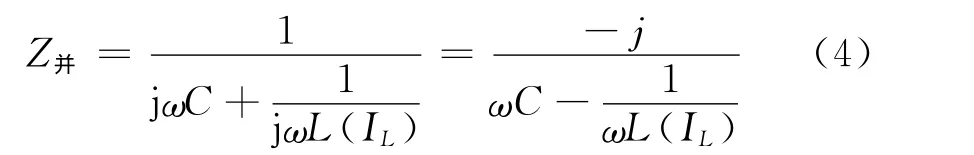

图2 铁磁谐振电路的工作点示意图Fig.2 Operation point diagram of ferroresonant circuit
这种非线性电感进入饱和,IL进一步增大,并与电容之间产生正反馈的充放电的过程即为铁磁谐振的物理本质。
若母线对地电容值较大,由于电容的放电作用,PT中的过电流和过电压值也较大,因此,黑启动过程中应使母线保持合理的对地电容。在实际电力系统中,线路的分散电容一般较小,合闸操作时,产生的过电流不足以引起铁芯线圈饱和;若为了提高功率因数,改善电能质量,而投入电容补偿装置,从而母线对地电容增大,合闸后产生的过电流就会增大,有可能使得铁芯线圈饱和,进入非线性区,从而发生铁磁谐振。因此,为了避免铁磁谐振的发生,在黑启动过程应把补偿电容切除掉;待黑启动过程完成后再逐步加入补偿电容,以避免铁磁谐振的发生。
2 铁芯线圈特性方程
通过实验测量可获得铁芯线圈的磁通φ与流过铁芯线圈电流IL之间的关系,即铁芯线圈的IL-φ特性曲线。为了获得PT电感值L和励磁电流IL之间的关系,即L-IL关系曲线,本文采用下述方法。
对于110kV线路PT,通过实验可测得铁芯线圈IL-φ关系为
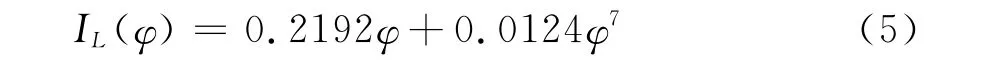

对于给定的一组φ与IL值,由式(5)和式(6),即可以绘制出非线性电感L-IL特性曲线,如图3所示。

图3 L-IL 特性曲线Fig.3 L-ILcharacteristic curve
根据图3所示的铁芯线圈的L-IL特性曲线,利用分段线性化,可得出分段函数L=L(IL),如式(7)。

可以看出,在IL≤0.07A时,非线性电感L处于线性阶段,其值为4.562H,当IL>0.07A时,非线性电感进入饱和区,其值随IL不断变化,从而可通过电感的励磁电流IL得到相应L。
3 天津电网黑启动关键路径的铁磁谐振分析
本文针对天津电网黑启动的关键路径,分析了550kV启动路径中安各庄站-安芦一线-芦台站部分、220kV启动路径滨海-滨疆一二-北疆电厂厂用电、内启动路径滨海电厂-葛沽母线三条路径。这3条路径作为天津电网黑启动中3个电压等级中最优路径,需对其进行铁磁谐振的分析。
3.1 内启动路径滨海电厂-葛沽母线
滨海内启动路径如图4所示,其线路数据如附录A中表A-1所示,由滨海电厂启动新军厂电厂。
滨葛线末端断路器合闸时,葛沽110kV母线的对地电容为新军葛线的分散电容的一半,约为0.106μF。其母线安装PT可利用式(7)所示函数处理。
利用PSCAD软件搭建黑启动关键路径及PT模型(用非线性电感模型代替),模拟线路末端断路器闭合时的电压电流情况。当线路末端断路器在0.305s时闭合,测得葛沽母线PT中电流的波形曲线分别如图5所示。
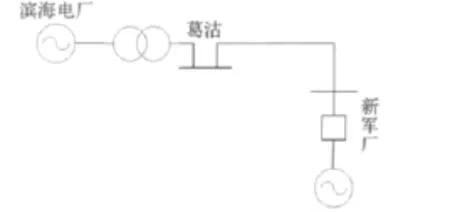
图4 滨海启动路径结构图Fig.4 Diagram of Binhai start path
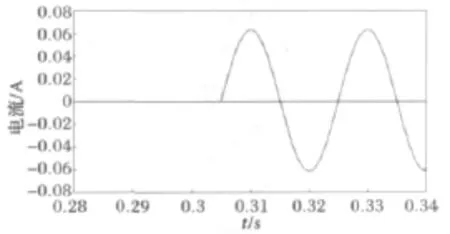
图5 葛沽母线PT中电流曲线Fig.5 Current curve in PT of Gegu bus
从图5可以看出,PT中电流仍处于未饱和阶段,即铁芯线圈仍处于线性阶段,未发生铁磁谐振。设在母线并联上补偿电容5μF,当0.305s断路器闭合时,测得PT中流过的电流如图6所示。

图6 有补偿电容时葛沽母线PT的电流波形Fig.6 Current curve in PT of Gegu bus including compensation capacitor
从图6中可以看出,加入补偿电容后,在断路器闭合时,由于电容放电作用,非线性电感中电流开始增大,进入饱和区,从而电感值减小,进一步增大电流和电压,并且非线性电感与电容之间不断充放电,发生了铁磁谐振现象。
3.2 550kV启动路径中安各庄站-安芦一线-芦台站部分
外启动中500kV最优启动路径如图7所示,其线路数据如附录A中表A-2所示,由安各庄向吴庄站和北郊站启动。
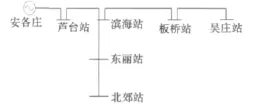
图7 外启动中500kV启动路径结构图Fig.7 Diagram of 500kV start path in external network start paths
安芦线末端的断路器合闸时,芦台站500kV母线的对地电容为滨芦线的分散电容的一半,为0.072μF。其母线安装PT的铁芯线圈IL-φ特性为IL=0.3626φ+0.03359φ9利用第3小节方法可得到500kVPT的L-IL特性关系式,如下式所示。
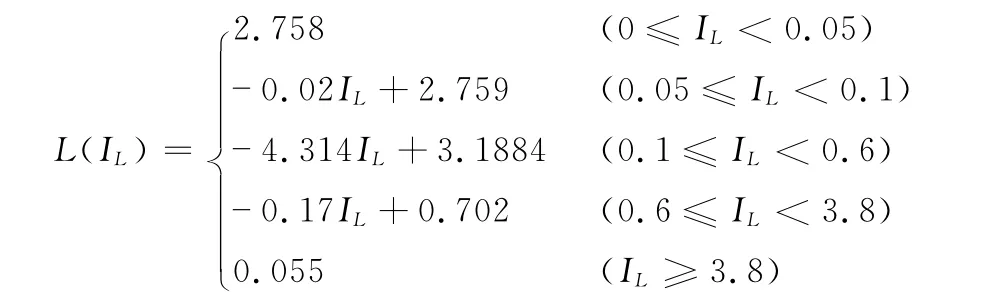
利用PSCAD软件搭建黑启动关键路径及PT模型(用非线性电感模型代替),模拟线路末端断路器闭合时的电压电流情况。当线路末端断路器在0.305s时闭合,测得PT中流入电流的波形曲线如图8所示。

图8 芦台站母线PT的电流曲线Fig.8 Current curve in PT of lutai bus
从图8可以看出,电流波形虽然产生了一定的波形畸变,但电流电压仍处于未饱和阶段,即铁芯线圈仍处于线性阶段,未发生铁磁谐振。设在母线并联上补偿电容7μF,在0.305s时断路器闭合,测得PT上流过电流如图9所示。
从图9中可以看出,加入补偿电容后,由于电容放电作用,非线性电感中电流增大,进入饱和区,使电感值减小,并且非线性电感与电容之间不断充放电,发生了铁磁谐振现象。
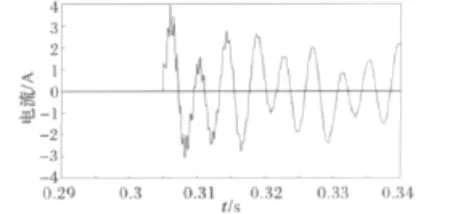
图9 有补偿电容时芦台站母线PT电流波形Fig.9 Current curve in PT of Lutai bus including compensation capacitor
3.3 220kV最优启动路径
外启动中220kV最优启动路径如图10所示,其线路数据如附录A中表A-3所示,由滨海500 kV主变启动北塘电厂。
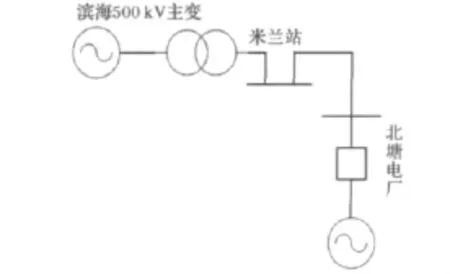
图10 外启动中220kV最优启动路径结构图Fig.10 Diagram of 220kV start path in external network start paths
滨米线末端断路器合闸时,北唐站220kV母线的对地电容为滨芦线的分散电容的一半,约为0.0285μF。其母线安装PT的铁芯线圈IL-φ特性为
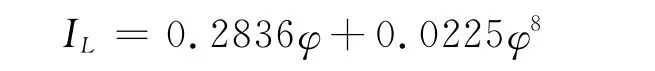
根据第3节方法将其分段线性化,可得220kV母线PT的L-IL关系式,如下:

利用PSCAD软件搭建黑启动关键路径及PT模型(用非线性电感模型代替),模拟线路末端断路器闭合时电压电流情况。当线路末端断路器在0.305s时闭合,测得PT中电流的波形曲线如图11所示。
从图11可以看出,虽然产生了一定的波形畸变,但电流电压仍处于未饱和阶段,即铁芯线圈仍处于线性阶段,未发生铁磁谐振。设在母线并联上补偿电容4μF,断路器闭合,测得PT中流过电流如图12所示。
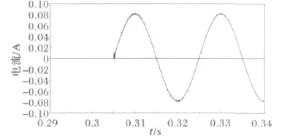
图11 北唐站母线PT电流曲线Fig.11 Current curve in PT of Beitang bus

图12 有补偿电容时北唐站母线PT的电流波形Fig.12 Current curve in PT of Beitang bus including compensation capacitor
从图12中可以看出,加入补偿电容后,在断路器闭合时,由于电容放电作用,非线性电感中电流开始增大,进入饱和区,从而电感值减小,进一步增大电流和电压,并且非线性电感与电容之间不断充放电,发生了铁磁谐振现象。因此,在黑启动过程应该把补偿电容切除,以避免铁磁谐振的发生。
4 结语
本文分析了母线电容对铁磁谐振的影响,得到了铁磁谐振的本质是电容及电感的充放电过程,及并联电容对非线性电流因电感的饱和而助增作用所导致的更为严重的过电流及过电压。
进而给出了在黑启动过程避免铁磁谐振发生的措施,即应切除并联电容器,待黑启动过程完成之后再投入相应的电容器。
天津电网最佳黑启动路径的铁磁谐振仿真分析结果验证了本文的上述结论。
附录A 天津电网三条最优启动路径的线路数据如表A-1至A-3所示。

表A-1 滨海启动路径输电线路参数Tab.A-1 Line parameters of Binhai start path
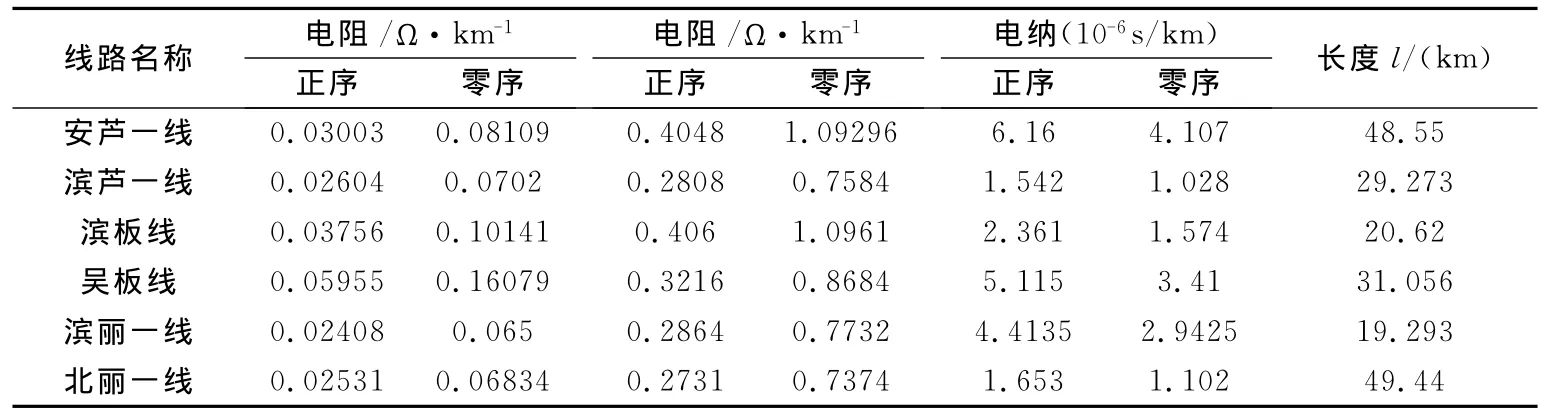
表A-2 500kV最优启动路径输电线路参数Tab.A-2 Line parameters of the optimal start path of 500kV

表A-3 220kV最优启动路径输电线路参数Tab.A-3 Line parameters of the optimal start path of 220kV
[1] Marti J R,Soudack A C.Ferro-resonance in power systems:fundamental solutions[J].IEE Proceedings-C,1991,138(4):321-329.
[2] Peterson H A.Transients in Power Systems[M].New York:John Wiley &Sons Inc,1951.
[3] Araujo A E A,Soudack A C,Marti J R.Ferro-resonance in power systems:chaotic behavior[J].IEE Proceedings-C,1993,140(3):237-240.
[4] Vukelja P I,Naumov R M,Vucinic M M,etal.Experimental investigations of overvoltages in neutral isolated networks[J].IEE Proceedings C,1993,140(5):343-350.
[5] 曹亚旭,邵鹏,张宏基,等(Cao Yaxu,Shao Peng,Zhang Hongji,etal).10kV母线PT高压保险熔断原因分析及解决措施探讨(PT 10kV high voltage busbar insurance fuse analysis and solving measures)[J].继电器(Relay),2007,35(S):405-408.
[6] 师立涛(Shi Litao).电力系统谐波谐振及防治措施的研究(Research on Harmonic Resonance and Prevention of Power System)[D].天津:天津大学电气与自动化工程学院(Tianjin:School of Electrical Engi-neering and Automation of Tianjin University),2010.
[7] 周丽霞,尹忠东,郑 立(Zhou Lixia,Yin Zhongdong,Zheng Li).配网PT铁磁谐振机理与抑制的试验研究(Research on principle of PT resonance in distribution power system and its suppression)[J].电工技术学报 (Transactions of China Electrotechnical Society),2007,22(5):153-158.
[8] 李云阁,施 围(Li Yunge,Shi Wei).应用解析法分析中性点接地系统中的工频铁磁谐振-谐振判据和消谐措施 (Study of fundamental ferroresonance on neutral-grounded systems by using analytical method-criterion and elimination)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(9):141-145.
[9] 李云阁,施围(Li Yunge,Shi Wei).应用解析法分析中性点接地系统中的工频铁磁谐振-非线性电感工频励磁特性的求取(Study of fundamental ferroresonance on neutral-grounded systems by using analytical method-solution to the power frequency excitation characteristic of nonlinear inductors)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(10):94-98.
[10] 汪伟,汲胜昌,曹涛,等(Wang Wei,Ji Shengchang,Cao Tao,et al).基波铁磁谐振理论分析及实验验证(Theoretical analysis and experimental verification of fundamental frequency ferroresonance)[J].电网技术(Power System Technology),2009,33(17):226-230.
[11] 周浩,余宇红,张利庭,等(Zhou Hao,Yu Yuhong,Zhang Liting,et al).10kV配电网铁磁谐振消谐措施的仿真比较研究(Comparative study on ferroresonance elimination measures in 10kV power distribution system by simulation method)[J].电 网 技 术(Power system technology),2005,29(22):24-34.
[12] 田璧元,俎云霄(Tian Biyuan,Zu Yunxiao).中性点绝缘电力系统中铁磁谐振的计算机仿真(Digital simulation of ferroresonance in neutral ungrounded power system)[J].华北电力学院学报(Journal of North China Institute of Electric Power),1990,(1):27-36.
[13] 石 启 新,谈 顺 涛 (Shi Qixin,Tan Shuntao).基 于MATLAB的电压互感器铁磁谐振数字仿真(Digital simulation analysis on ferroresonance of electromagnetic potential transformer based on MATLAB)[J].高电压技术(High Voltage Engineering),2004,30(8):25-27,49.
[14] 杨秋霞,宗伟,田璧元(Yang Qiuxia,Zong Wei,Tian Biyuan).基于小波分析的铁磁谐振检测(Detection of ferromagnetic resonance based on wavelet analysis)[J].电网技术(Power System Technology),2001,25(11):55-57,61.
