计及网络参数不确定的含风电场安全经济调度
2012-11-09童小娇
唐 民, 童小娇,2, 文 强
(1.长沙理工大学电气与信息工程学院, 长沙 410004;2.衡阳师范学院, 衡阳 421002; 3.衡阳电业局, 衡阳 421001)
计及网络参数不确定的含风电场安全经济调度
唐 民1, 童小娇1,2, 文 强3
(1.长沙理工大学电气与信息工程学院, 长沙 410004;2.衡阳师范学院, 衡阳 421002; 3.衡阳电业局, 衡阳 421001)
基于线性鲁棒优化方法提出了一种计及风电场出力及线路参数不确定性的电力系统安全经济调度模型,该模型计及了系统运行时风电场出力及线路参数的不确定性对线路安全的影响,利用线性鲁棒优化理论构建调度模型,并运用优化对偶理论对其进行简化。根据本文所构建的模型可得到一个不确定安全经济调度区域(USEDR),独立系统运行员(ISO) 基于安全性和经济性合理确定系统扰动指标在该区域进行调度。最后,以改进的IEEE-30节点系统为例,检验了所构建模型的合理性及可行性。
风电场; 不确定性; 经济调度; 鲁棒优化; 安全
近年来,随着我国能源结构的不断调整,风力发电逐渐显示出广阔的应用前景。随着科学技术的不断进步,大量新型风电场的容量可以与常规机组媲美[1~4]。由于风能的可再生性,利用它来发电可以为电力系统节省燃料成本[5],但是风能具有随机性,大型风电场并入电力系统中,使得电力系统运行的不确定性因素也随之增加[5~8]。因此,有关大型风电场并网后的研究工作也越来越受到重视,尤其是对大型风电场并网后的安全经济调度研究工作带来了巨大的挑战。
风电是不可控制的随机变量,它不能像常规电源那样进行经济调度[9,10],风电并网时会带来附加惩罚成本,如增加发电机组的旋转备用、安全成本等[10]。风电的随机性还将加大电力系统调频的不确定性,影响电能的质量[9,11]。电力系统本身就是一个庞杂的系统,运行时受大量不确定性因素的影响(如空气温度、湿度、系统运行时频率波动、负荷波动等),这些不确定性因素都会给电力网络参数甚至是系统安全造成影响,经典经济调度都是基于确定性因素进行分析,并没有考虑这些不确定性因素的影响。电力系统为了追求最大的经济利益,在进行经济调度时,尽可能充分利用现有的电网线路,使得部分线路运行接近临界状态,而风电场的并网对电网的安全运行带来越来越大的挑战[6]。因此,计及不确定因素的影响,构建大型含风电场电力系统的安全经济调度模型有待进一步研究。
文献[12,13]是在确定的安全约束域内寻求经济性目标的最优解,并没有考虑不确定性因素对电网安全水平所造成的影响。文献[4,14,15]假设风电场功率因数为确定量,通过给定的风速计算出风电机组的有功功率和无功功率,但实际风电场的风速是难以精确预测到的,而是在预测值的基础上存在不确定性。文献[16]根据风电机组的有功功率和无功功率近似二次函数的关系来计算无功功率。由于风电机组吸收无功功率的大小与机端电压输出的有功功率及滑差密切相关,因此,上述方法并不能准确反应风力发电的实际情况。文献[5]应用模糊理论建立了含风电场的电力系统动态经济调度模糊模型,并对传统粒子群算法进行改进用于求解提出的问题。虽然部分解决了风电场输入功率难以准确预测而对传统机组的经济调度带来的困难,但并没有解决线路参数的不确定性以及风电场输入功率不确定性所带来的安全越限问题。文献[17]考虑风电场出力的不确定性,利用随机优化方法构建了经济调度模型,该模型最终被转化为一个确定性的模型,并利用混合整数线性规划法求解。但该方法预测的风电场出力与风电场实际出力有一定的差距,且还需假设风电场出力的概率函数为正态分布。
为了克服上述方法的不足与缺陷,本文在经典经济调度模型的基础上进一步考虑风电场出力的不确定性以及网络参数的不确定性,构建更为贴切实际的模型,并通过该模型选择多种波动指标进行常规机组的经济调度,也有利于电力系统安全运行。在处理这种不确定性的问题时,线性鲁棒优化理论是处理这类问题较好的方法,它不需要假定模型分析时某种状态的概率分布,且能考虑最坏(Worst-case)情况下的运行状态。因此,本文利用鲁棒优化方法对电力系统中风电场出力的不确定性及网络参数的不确定性进行描述,模拟仿真表明该方法的有效性。
1 安全经济调度模型
1.1 数学模型
由于风力发电不需要消耗燃料,电力公司首先调度的应该是全部风电,所以目标函数中机组不包括风电机组,以常规机组耗量成本为最小作为优化目标,目标函数为
(1)
式中:F(Pg)为系统总发电费用;Ng为常规发电机的总数;Pgi为第i台发电机的输出有功功率;ai、bi和ci为成本函数的系数。
在电力系统安全经济调度中还有一些约束,如发电机运行约束、功率平衡约束、线路容量约束等。如下所示:
(1)发电机运行约束

(2)
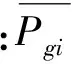
(2)功率平衡约束
(3)
式中:PL∑为系统总网损,可采用系统总负荷的百分值估算或B系数法计算;PD为系统总负荷;Pwj为第j个风电场输出的有功功率;Nw为系统中风电场总数。
(3)线路安全约束

(4)
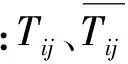
1.2 线路潮流计算
本文中电力系统中含有Ng+Nsl个发电机节点(Ng个PV节点和Nsl个平衡节点)和Nd个负荷节点(PQ节点),故电力系统共有N=Ng+Nsl+Nd个节点,系统中有L条支路。文献[18]给出了交流潮流模型,在节点i的有功和无功注入功率如下所示。
(5)
(6)
式中:Vi和θi(θij=θi-θj)分别指节点电压及其相角。Gij和Bij分别指线路i-j的电导和电钠。Pi和Qi分别指节点输入的有功和无功功率。
利用快速分解法(fast decoupled load flow)的思路,即认为有功功率受电压相角的影响,而无功功率主要受电压幅值的影响,忽略了电压幅值对有功功率的影响及电压相角对无功功率的影响。在此基础上假设sinθij≈θi-θj,cosθij≈1,Vi=1.0 p.u.(i=1,2,…,N),这样,电力网络模型就成为线性网络模型。本文假定电力网络的功率因数恒定不变,即cosφ=k为常数。这样,式(5)和(6)就可以用两个矩阵表示如下:
ΔP=HΔθ
(7)
ΔQ=-LΔVd
(8)
其中:ΔP=[ΔPg,ΔPd],ΔQ=[ΔPg,ΔPd]tanφ,ΔPg和ΔPd分别指发电机输入功率和负荷输入功率的增量矩阵,Δθ和ΔVd分别指节点相角的增量和负荷节点电压的增量。式(7)和式(8)又可以改写成如式(9)和式(10)的形式,即
Δθ=H-1ΔP
(9)
(10)
式(9)和式(10)中
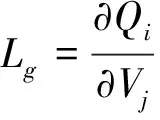
Bb,ij=-1/Xb,ij
j,m=1,2,…,Nd
其中:Hij和Lij分别指代的是矩阵H和L中的第i行第j列的值。而Lg和Ld为矩阵L的子矩阵。j∈a指连接第j个节点的集合,Xb,ij为连接节点i和节点j上的支路的电抗。
文献[18]给出了线路i-j的支路潮流方程:
(11)
Bb,ijcosθij)
(12)
把式(11)和式(12)类似的像处理式(5)和式(6)一样,并结合式(9)和式(10)便可以得到
(13)
(14)
其中:
以上诸式中,Dij和Eij分别指代的是矩阵D和E中的第i行第j列的值。而Dg和Dd、Hg和Hd、Eg和Ed分别为矩阵D、H、E相对应的子矩阵。
由于系统网络处理成线性网络了,于是可得到支路上的有功及无功潮流的方程为
Pb=SgPg+SdPd
(15)
Qb=Sv,gPg+Sv,dPd
(16)
其中:Sg、Sv,g和Sd、Sv,d分别指发电机有功功率的灵敏度矩阵和负荷有功功率的灵敏度矩阵。Pg=[Pg1,Pg2…PgNG]T和Pd=[Pd1,Pd2…PdNd]T分别指发电机出力和负荷功率矩阵。
2 线性鲁棒优化理论
2.1 线性鲁棒优化模型
20世纪70年代Soyster提出线性规划鲁棒优化模型[19],鲁棒优化是解决内部结构和外部环境不确定情况下的优化方法。鲁棒优化解决内部结构变动问题时,对于数学规划问题而言,一种是约束条件参数的不确定性,一种是目标函数参数的不确定性[20],本文的问题是约束条件参数的不确定性。
鲁棒优化已经从Soyster的线性优化鲁棒方法,发展到目前鲁棒优化理论的经典体系。Tal,Nemirovski,Ghaoui和Lebret等学者在建立鲁棒优化理论方面进行了重要工作,他们研究的是具有不同形式的数据不确定性的线性规划问题、二次规划问题和半定规划问题等。本文涉及到线性鲁棒优化问题[19,21,22]。
一般鲁棒优化定义如下:
(17)
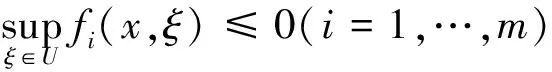
(18)
线性规划定义如下:
(19)
记A={a1,a2,…,am}T,b={b1,b2,…,bm}T其中ai为约束矩阵A的第i行,则式(19)可写为

(20)
假设a1∈U1,a2∈U2,…,am∈Um其中Ui(i=1,2,…,m)为不确定集合,目标函数中系数C的不确定性可以归纳为约束矩阵的不确定性。式(20)鲁棒对应:
minCTx
s.t.aix≤bi,∀ai∈Ui(i=1,…,m)
(21)
易知aix≤bi,∀ai∈Ui(i=1,…,m)等价于求解如下问题:
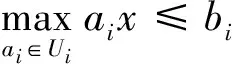
(22)
式(22)的复杂性决定鲁棒优化问题的复杂性。
2.2 集合U的确定与计算原则
鲁棒优化问题的关键是不确定集合U的确定以及在某给定U下复杂min-max模型的化简,实际计算的可操作性,本文考虑'盒式'不确定集合,即设参数U具有如下形式:
(23)
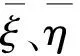
Soyster针对一般线性规划模型的约束矩阵列的不确定性,设计了一套鲁棒优化方法。首先,对于任意一个不确定的数据元素,设计基于数据元素的标称值的一个可能的有界对称区间,通过引入随机变量消除标称值,使得数据元素变成完全不确定的,然后,在原来的线性规划模型的基础上,对每个不确定数据元素引入决策变量,在标准形式的约束方程的左端添加不确定性数据的最大值与引入变量的乘积。这样,原问题的鲁棒对应仍然是线性规划问题,但消除了数据元素的不确定性[19]。这样,就可以用一般的方法来解决本文的问题。
3 不确定性因素对线路安全的影响
3.1 风电场出力的不确定性
本文假定在第j个节点上有大型风电场并网,即Pg,j=Pw+ξ,其中ξ是不确定的随机量,Pw是风电预测出力,是一个确定量。考虑式(3)的功率平衡约束,式(15)可以写成如下形式:
Pb(Pg,ξ)=Sg(Pg1,Pg2,…,Pgi,…,PgNG)T+
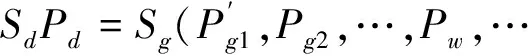
PgNG)T+SdPd+(Sg0j-Sg01)ξ
(24)
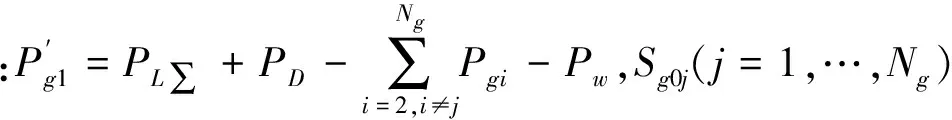
Pb(Pg,ξ)≤Tmax
(25)
根据鲁棒优化理论,上式等效于求解
(26)
上式综合式(24)即得:
(27)

Li(ξ,z,δ,γ)=-(Sgij-Sgi1)ξ-ziξ+
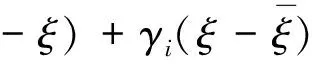
(28)
对上式求导后得
ΔξLi(ξ,z,δ,γ)=-(Sgij-Sgi1)-
zi-δi+γi=0
(29)
又
(30)
于是可整理,得
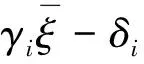
(Sgij-Sgi1)+zi+δi-γi=0
δi≥0,γi≥0
(31)
式(31)写成矩阵形式如下:
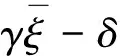
(Sg0j-Sg01)+z+δ-γ=0
δ≥0,γ≥0
(32)
式(32)即为只考虑风电场出力的不确定性的线路安全约束。
3.2 考虑网络参数不确定性的含风电场
本文3.1中仅仅只考虑了风电场出力的不确定性,本节将在本文3.1的基础上进一部考虑网络参数的不确定性,电力系统是一个庞大而又复杂的系统,由于环境温度、空气湿度、系统运行时频率的不稳定性及负荷波动等不确定性因素的影响,将会导致网络参数不确定性的变化,由本文1.2中知道,网络参数的不确定性最终改变的是线性网络的灵敏度,于是由式(15)得:
(S+ΔS)P′T
(33)

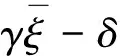
SP′T+κ+u-v=0,u≥0,v≥0
(Sg0j-Sg01)+z+δ-γ=0
δ≥0,γ≥0
(34)
式(34)表示在考虑风电场出力不确定性的同时还考虑网络参数不确定性的线路安全约束,即为式(4)的等价。
综上所述,本文所求解的模型是由式(1)的目标函数及式(2)和式(34)所确定的约束函数组成。
4 数值仿真
4.1 仿真系统
为验证本文所建模型和算法的有效性,本文对修改后的IEEE 30节点系统进行数值测试,网络的负荷、发电机的数据等见文献[23],二次成本函数见文献[23],单位为£/h。为了方便起见,有关发电机的数据重新列在表1中。
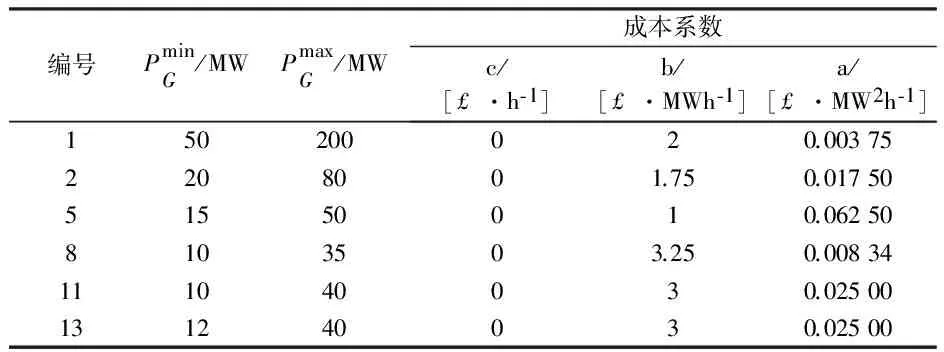
表1 发电机参数
4.2 最优解F(Pg)和PG的扰动情况
本文以系数波动参数ξ和η的取值如下:
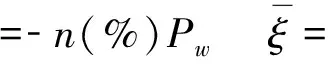
(35)
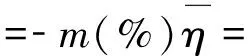
(36)
为使线路安全性得到突出,以突出不确定性对线路安全的影响,设置线路所能承受的最大潮流容量比正常运行时略高且风电预测出力Pw=5.7 MW。
图1显示出在不同的网络参数波动系数m下总发电费用随n的变化而波动,图2~7显示出在不同的网络参数波动系数m下各机组出力随着n的变化而波动。(注:以下各图中其中有大部分曲线相重叠而无法分辨出来,其实每个图都应是八条曲线。若曲线发生重叠则说明网络参数在该波动指标下对其机组出力影响不大。)
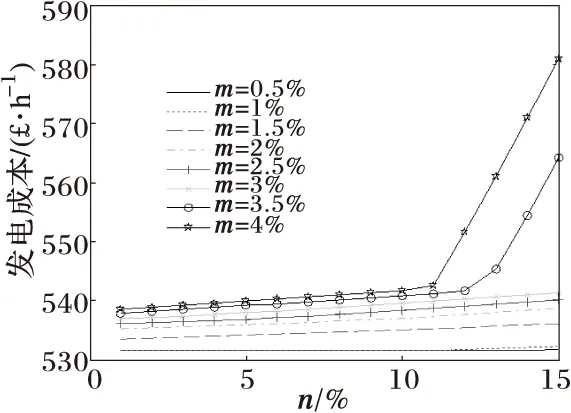
图1 随n和m的变化发电成本的变化
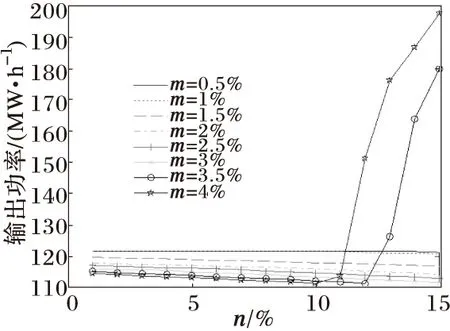
图2 随n和m的变化机组1的出力变化
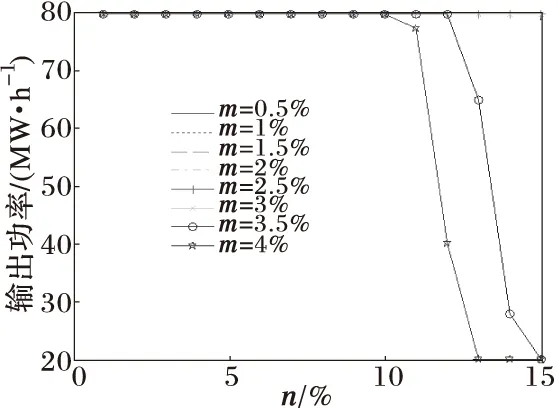
图3 随n和m的变化机组2的出力变化
上述每个图中的曲线代表的是当网络参数的波动量在m时各发电机的出力(或发电成本)随风电场出力的波动n的变化而形成的曲线(如图1中最上面的一条曲线就代表当网络参数的波动量在4%时,发电成本随风电场出力的波动n的变化而形成的一条曲线)。由图1中可以看出,当网络参数和风电输入功率共同波动幅度越大,发电成本就越多,图1中,当网络参数波动量分别在4%和3.5%,风电场出力波动随n增加分别至11%和12%以后,发电成本显著增加,而网络参数波动量在3%及其以下时,发电成本并未出现显著的增加。这是由于网络参数波动过大,为了保证线路安全,就必须对发电机重新进行较大的分配以保证系统安全运行,从图2至图7可以看出在相应的波动下发电机的出力的发生了较大的变化,这相当于为保证电网安全运行的再调度.若要使其发电成本不显著增加,通过增大线路容量即可。
由此可见,线路容量在设计时,可以通过本文所叙的方法,充分考虑不确定性因素的影响,设计的线路比网络正常运行时高一定量即可,使系统运行能够充分利用电力线路而又保证线路安全。其中图5显示的机组8并没有随波动有所改变,说明机组8按照恒定功率出力运行,风电场出力和电网线路参数的波动对系统运行没有影响。图3和图4也说明了机组2和机组5在风电场出力波动不大的时候机组出力恒定,同时网络参数的波动对其没有影响。图1还反映出若能有效的抑制波动,将会为电力系统运行节省成本。
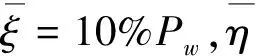
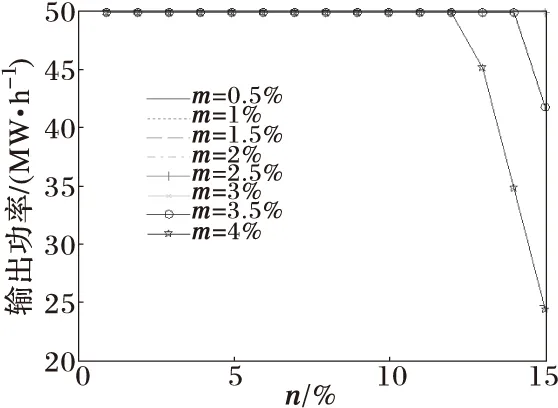
图4 随n和m的变化机组5的出力变化
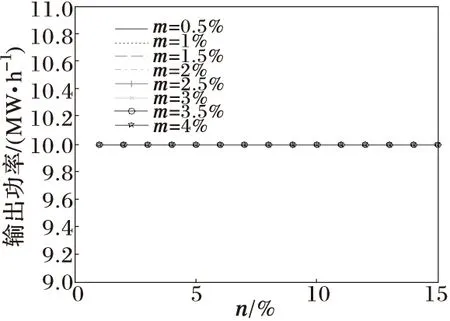
图5 随n和m的变化机组8的出力变化
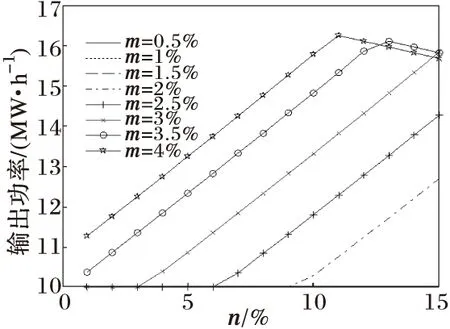
图6 随n和m的变化机组11的出力变化
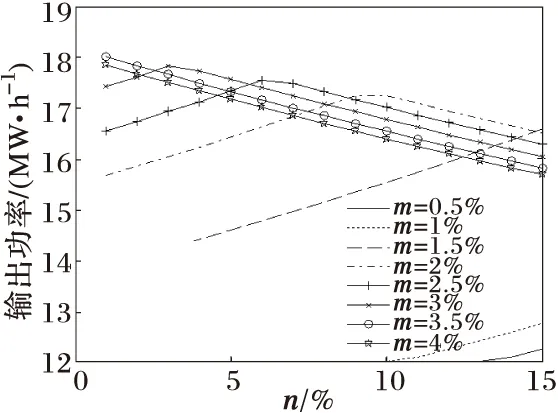
图7 随n和m的变化机组13出力的变化
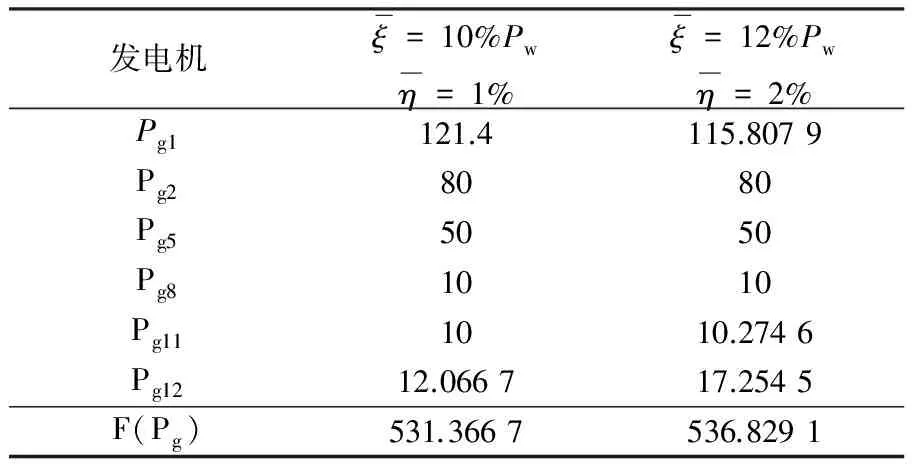
表2 不同扰动指标的调度值
本文所得的发电成本结论与文献[17]一致,当考虑风电场出力不确定性时都会使发电成本增加。本文所得的结果将更加趋于保守,较文献[17]来说,本文无须假定风电场出力的分布,而且可以根据实际情况灵活选择波动值进行调度。
5 结语
本文提出了一种考虑电力系统运行不确定性因素影响的情况下,应用鲁棒优化理论进行计算的经济调度模型,该模型最后得出了一个不确定安全调度区(USEDR),在该不确定安全经济调度区,通过合理选择不确定性指标便能得出该指标下的经济调度最优值,同时最大限度地保证了系统运行的安全性。根据在IEEE-30节点的仿真表明,该模型还能应用在安全成本代价最小的计算中,只要改变本文的目标函数以及约束函数中发电机功率用再调度发电机功率代替即可。
[1] 孙元章,吴俊,李国杰(Sun Yuanzhang,Wu Jun,Li Guojie ).风力发电对电力系统的影响(Influence research of wind power generation on power systems)[J].电网技术(Power System Technology),2007,31(20):55-62.
[2] 尹明,王成山,葛旭波(Yin Ming,Wang Chengshan,Ge Xubo).风电并网经济技术评价研究综述(Review of economic-technical assessment of wind power integration)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(5):102-108.
[3] 戴慧珠,王伟胜,迟永宁(Dai Huizhu,Wang Weisheng,Chi Yongning).风电场接入电力系统研究的新进展(Recent wind power integration study in China)[J].电网技术(Power System Technology),2007,31(20):16-23.
[4] 顾承红,艾芊(Gu Chenghong,Ai Qian).基于改进内点法的含风电场的系统最优潮流计算(Optimal power flow calculation based on the improved interior method for a system integrated with wind farms)[J].中国电力(Electric Power),2007,40(1):89-93.
[5] 陈海焱,陈金富,段献忠(Chen Haiyan,Chen Jinfu, Duan Xianzhong).含风电场电力系统经济调度的模糊建模及优化算法(Fuzzy modeling and optimization algorithm on dynamic economic dispatch in wind power integrated system)[J].电力系统自动化(Automation of Electric Power Systems),2006,30(2):22-26.
[6] 张丽英,叶廷路,辛耀中,等(Zhang Liying, Ye Tinglu, Xin Yaozhong,etal).大规模风电接入电网的相关问题及措施(Problems and measures of power grid accommodating large scale wind power )[J].中国电机工程报(Proceedings of the CSEE),2010,30(25):1-9.
[7] 袁铁江,晁勤,吐尔逊·伊不拉音,等(Yuan Tiejiang,Chao Qin,Tu Erxun Yibulayin,etal). 电力市场环境下含风电机组的环境经济调度模型及其仿真(An environmental/economic dispatch model for power grid containing wind power generation units and its simulation in electricity market environment)[J].电网技术(Power System Technology),2009, 33(6):67-71.
[8] Jianghui Wang, Shahidehpour M ,Zuyi Li. Security-constrained unit commitment with volatile wind power generation[J]. IEEE Trans on Power Systems,2008,23(3):1319-1327.
[9] 雷亚洲,王伟胜,印永华,等(Lei Yazhou,Wang Weisheng,Yin Yonghua,etal).一种静态安全约束下确定电力系统风电准入功率极限的优化方法(An optimization method for determining wind power penetration limit in power system under static security constraints)[J].中国电机工程学报(Proceedings of the CSEE),2001,21(6):25-28.
[10]丁明,吴义纯(Ding Ming,Wu Yichun).风力发电系统运行和规划问题研究综述(Summary on studies of operation and planning of wind Power generation systems)[J].电网技术(Power System Technology),2003,7(3):36-40.
[11]胡文锦, 武志刚, 张尧,等(Hu Wenjing,Wu Zhigang,Zhang Rao,etal).风电场电能质量分析与评估(Analysis and evaluation on the electric power quality of the wind farm)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(4):82-87.
[12]Xiao Fei,McCalley James D.Risk based multi-objective optimization for transmission loading relief strategies[C]∥Power Engineering Society General Meeting,Tampa,USA: 2007.
[13]Xiao Fei,McCalley James D.Risk-based security and economy trade off analysis for real-time operation [J].IEEE Trans on Power Systems,2007,22(4):2287-2288.
[14]Papadopoulos M, Malatestas P, Hatziagyriou N. Simulation and analysis of small and medium size power systems containing wind turbines[J].IEEE Trans on Power systems,1991,6(4):1453-1458.
[15]Saad-Saoud Z,Jenkins N.Models for predicting flicker induced by large wind turbines [J].IEEE Trans on Energy Conversion,1999,14(3):743-748.
[16]El-Sadek M Z,Dessouky M M,Mahmoud G A,etal.Load representation for steady-state voltage stability studies[J].Electric Power System Research,1997,43(3):187-195.
[17]Yan Yong,Wen Fushuan, Yang Shouhui,etal. Generation scheduling with fluctuating wind power[J].Automation of Electric Power Systems,2010, 34(6):79-88.
[18]张伯明,陈寿孙.高等电力网络分析[M].北京:清华大学出版社,2007.
[19]Soyster A L. Convex Programming with Set-Inclusive constraints and applications to inexact liner programming [J]. Operations Research, 1973, 21(5): 1154-1157.
[20]徐家旺, 黄小圆(Xu Jiawang,Huang Xiaoyuan). 鲁棒优化及其应用研究的进展(Advance in research on robust optimization and application)[C]∥2005中国控制与决策学术年会(Control and Decision 2005 Annual Conference of China),哈尔滨(Harbin),中国(China):2005.
[21]Ben-Tal A, Nemirovski A. Robust solutions to uncertain liner programs [J].Operations Research Letters,1999,25(1):1-13.
[22]Ben-Tal A, Nemirovski A. Robust solutions of liner programming problems contaminated with uncertain data[J].Mathematical Programming,2000,88(33):411 -424.
[23]Alsac O, Stott B. Optimal load flow with steady-state security[J].IEEE Trans on Power Apparatus and Systems, 1974,93(3):745-751.
唐 民(1986-),男,硕士研究生,研究方向为电力系统优化、运行与控制。Email:tomtang610@yahoo.com.cn
童小娇(1962-),女,教授,博士生导师,研究方向为最优化理论与计算方法、电力市场、电力系统分析等。Email:ongxj@csust.cn
文 强(1982-),男,硕士研究生,研究方向为电力系统规划与运行。Email:wenqiang822@nwsuaf.edu.cn
SecurityEconomicDispatchofPowerSystemIntegratedwithWindFarmsConsideringUncertaintyofNetworkParameters
TANG Min1, TONG Xiao-jiao1,2, WEN Qiang3
(1.College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410004, China;2.Hengyang Normal University, Hengyang 421002, China;3.Hengyang electric power supply bureau, Hengyang 421001,China)
Based on linear robust optimization approach, a model was proposed for the security economic dispatch of power system considering the outputs of wind farms and the uncertainty of line parameters. The impacts of wind power output and the uncertainty of line parameters on the operating safety of power line was investigated. The theory of linear robust optimization was utilized to build the scheduling model, and then the optimization duality theory was used to simplify the model. By using this model, an uncertain security economic dispatch region (USEDR) can be obtained. Based on the security and economy, the independent system operator (ISO) can reasonably determine the system disturbance indicators to carry out the schedule in this region. Finally, by taking the improved IEEE-30 nodes power system as an example, the rationality and feasibility of the model were demonstrated.
wind farms; uncertainty; economic dispatch; robust optimization; security
TM715
A
1003-8930(2012)02-0027-08
2011-04-01;
2011-05-03
国家自然科学基金资助项目(10926189,10871031);湖南省自然科学衡阳联合基金资助项目(10JJ8008);湖南省教育厅重点项目资助项目(10A015)
