支持向量机结合TLS-ESPRIT的间谐波参数估计

李 新， 陈文礼， 侯兴哲， 付志红， 苏向丰

(1.重庆大学输配电装备及系统安全与新技术国家重点实验室， 重庆 400044；2.重庆电力科学试验研究院， 重庆 401123)

支持向量机结合TLS-ESPRIT的间谐波参数估计

李 新1， 陈文礼1， 侯兴哲2， 付志红1， 苏向丰1

(1.重庆大学输配电装备及系统安全与新技术国家重点实验室， 重庆 400044；2.重庆电力科学试验研究院， 重庆 401123)

为精确估计间谐波信号参数，提出支持向量机(SVM)结合总体最小二乘旋转不变子空间(TLS-ESPRIT)算法的间谐波分析方法。首先对由采样数据形成的HANKEL矩阵进行奇异值分解(SVD)，运用总体最小二乘法(TLS)求解旋转关系方程，获得电网信号的频率参数；然后通过支持向量机算法估计出间谐波信号的幅值和相位参数。仿真结果表明，该方法能够精确估计间谐波信号的各项参数，不仅减小了单独使用SVM算法的计算量，而且在低信噪比条件下，具有良好的稳健性。

间谐波； 奇异值分解； 总体最小二乘旋转不变子空间； 支持向量机； 稳健性

间谐波是指电压和电流信号中存在的频率为工频非整数倍的信号分量。近年来随着电网中非线性负载与电力电子装置的大量使用，间谐波污染引起的电能质量下降不断加剧[1]。快速准确的谐波和间谐波检测是提高电能质量的前提。

傅里叶变换用于间谐波参数估计无法避免频谱泄露和栅栏效应，对同步采样和频率分辨率要求较高[2]。文献[3]利用加窗插值FFT修正算法克服了这一缺点，但对分析窗的宽度要求较高，无法满足实时性要求。小波变换[4]具有较好的局部化特性，但不同尺度的小波函数在频域上存在相互混叠，不能很好地检测出频率相近的谐波或者间谐波。基于神经网络的间谐波参数估计[5]需要大量样本数据，计算量较大，实时性较差。

旋转不变子空间ESPRIT(estimation of signal parameters via rotational invariance techniques)算法[6，7]是现代谱估计算法[7～11]中的典型算法，最早用于阵列信号处理，主要优点在于计算量小，避免了谱峰搜索。TLS-ESPRIT算法是ESPRIT的改进算法，近年来被用于电力系统谐波参数估计，在低信噪比的情况下具有较好的频率估计性能。

支持向量机[12，13]用于间谐波检测具有精度高、稳健性好的优点，但在频率未知且需要较高频率分辨率的情况下，计算量较大。

本文首先利用TLS-ESPRIT算法精确估计出信号的频率参数，再结合支持向量机方法估计信号的幅值与相位参数，在保证估计精度的同时，减小单独运用SVM算法的计算量。

1 TLS-ESPRIT频率估计原理

电压或电流采样信号可以表示为

(1)

式中：P为信号的频率成分数；αk、φk、ωk分别为第k个谐波或间谐波分量的幅值、初相角和频率；w(n)为第n个信号采样点中的噪声分量。

为了便于利用TLS-ESPRIT算法估计频率参数，首先通过欧拉变换将式(1)表示的实信号转换为复信号模型，即

(2)

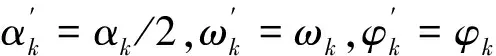
定义一个长度为L的由信号采样延迟组成的时间窗

X(n)=[x(n)，x(n+1)，…，x(n+L-1)]T

(3)

根据式(2)的描述模型式(3)可以表示为

X(n)=S(n)+W(n)=AIΦnα+W(n)

(4)

式中：S(n)=ALΦnα=[s(n)，…，s(n+L-1)]T；

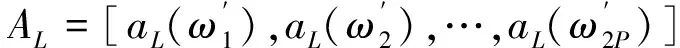
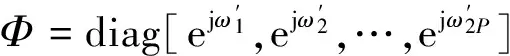
W(n)=[w(n)，w(n+1)，…，w(n+L-1)]T。

去掉S(n)的第一行和最后一行，得到两个相互交错的矢量S1和S2为

(5)

S1=AL-1Φnα=A1α

S2=AL-1Φn+1α=A2α

A2=A1Φ

信号的频率信息包含在旋转因子矩阵Φ中，TLS-ESPRIT算法就是利用信号子空间的旋转不变性，在总体均方误差最小的约束下估计出旋转因子矩阵 ，从而获得信号的频率参数。根据信号子空间估计方法的不同，该算法的实现形式多种多样，本文通过对采样数据矩阵进行SVD分解来获取信号子空间，避免信号相关矩阵的计算，实现信号频率的快速，精确估计，其具体实现步骤如下。

步骤1对信号采样，构造数据矩阵

(6)

式中：Lgt;2P，Mgt;2P，M+L-1=N。

步骤2对X进行奇异值分解

(7)

式中：L为左奇异矢量矩阵；U为右奇异矢量矩阵；Σ为降序排列的奇异值对角矩阵；Us为2P个最大奇异值对应的右奇异矢量矩阵，张成信号子空间，Un为L-2P个最小奇异值对应的右奇异矢量矩阵，张成噪声子空间。

步骤3去掉Us的第一行和最后一行，得到两个相互交错的子空间U1和U2，令U2=U1Ψ，考虑U1、U2同时存在误差，利用总体最小二乘思想[14]，对矩阵[U1，U2]进行奇异值分解得

(8)

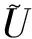
(9)

则有

(10)

步骤5对ΨTLS进行特征值分解，特征值λk即为旋转因子矩阵Φ的对角元素，由此估计出信号的频率参数

(11)

2 基于SVM的幅值和相位估计

为便于利用SVM算法估计幅值和相位参数，首先将式(1)表示的模型变形为

(12)

式中：Ck=αkcosφk；Dk=αksinφk。噪声分量w(n)为模型误差，记为en。

采用和文献[15]相同的方法，可以得到迭代变权最小二乘法格式为

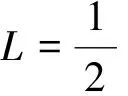
(13)

(14)

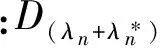
求得W后，信号的幅值和相位参数可由Ck和Dk求得，即

(15)

φk=arctan(Dk/Ck)

(16)

由TLS-ESPRIT算法估计出信号的频率参数，可以将矩阵Y的维数确定为最小，避免了在很大的频率范围内进行频率搜索，大大减小单独使用SVM算法的计算量。

3 仿真和实例分析

3.1 间谐波参数估计仿真分析

实际电网信号谐波和间谐波分量幅值较小[16]。为了验证本文所提间谐波参数估计算法的性能，模拟电网信号

x(t)=1.7cos(2πg45t+20°)+

100cos(2πg50.1t+30°)+

1.4cos(2πg115t+40°)+

2cos(2πg150t+60°)+

1.23cos(2πg175t+45°)+w

(17)

基波频率为50.1 Hz，各次谐波和间谐波幅值都控制在基波幅值的2%以内。采样频率为1 000 Hz，采样点数为200，约10个基波周期。 为SNR=20 dB的高斯白噪声。设c=0.5，ε=0.01(本文所有算例c和ε均采用此设置)。用本文提出的算法进行参数估计仿真，估计结果如表1所示。

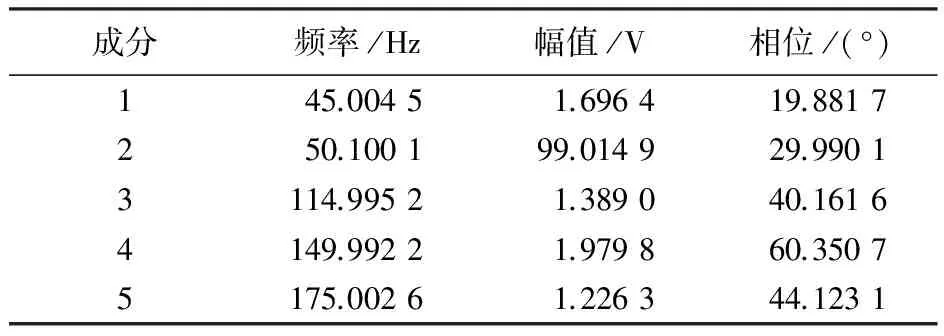
表1 仿真信号参数估计结果

从仿真估计结果可以看出，本文所提出的间谐波参数估计方法即使在低信噪比的情况下，也可以较为精确地估计出含有多次谐波和间谐波成分的电网信号参数。

频率估计的精度直接影响SVM幅值和相位估计的准确性。在上例中，如果间谐波分量115 Hz估计出现偏差，其余频率分量估计准确，则SVM估计出该间谐波所对应的幅值和相位如表2所示。仿真结果表明，TLS-ESPRIT算法的高精度频率估计保证了SVM幅值和相位估计的准确性。

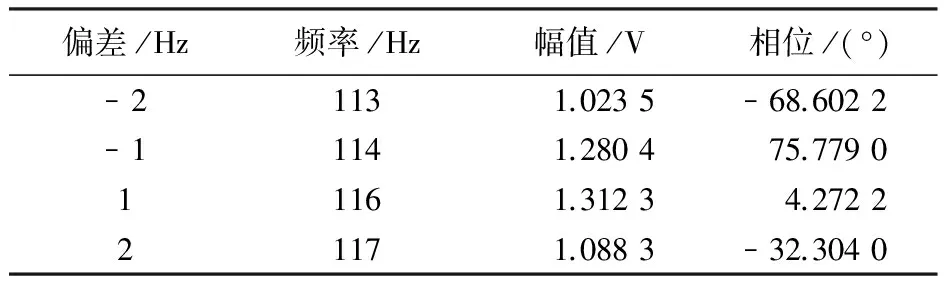
表2 频率估计对SVM的影响

3.2 实际数据分析

文献[17]提供了一台未安装补偿装置的电弧炉的电流波形数据，含有50 Hz、125 Hz、25 Hz频率分量和5%的随机噪声。采用本文方法对其进行参数估计，采样频率为1 000 Hz，采样点数为100，约5个基波周期。估计结果如表3所示，估计参数拟合波形与原始信号波形对比如图1所示。同时采用Burg算法对其进行分析，结果如图2所示，可以看出Burg算法不仅出现了谱线偏移，而且出现了120 Hz的虚假频率分量。

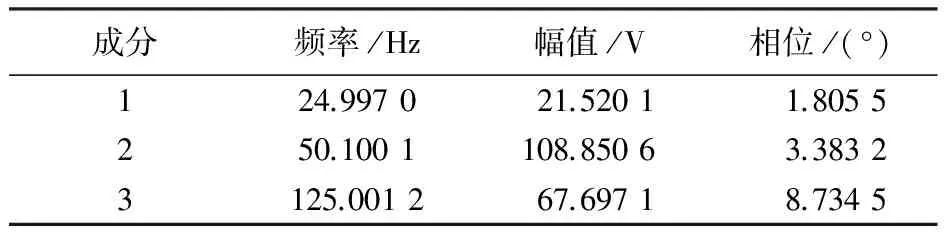
表3 频谱参数估计结果

图1 拟合波形和原始信号对比

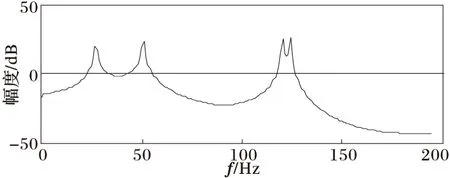
图2 Burg算法频谱估计结果

4 结语

TLS-ESPRIT算法可以在低信噪比的电网信号中精确估计出频率参数，对噪声不敏感,所需采样时间短，SVM算法可以消除异常值的影响，具有良好的稳健性，仅需要小样本数据。将两者结合用于谐波和间谐波参数估计具有良好的估计效果，抗噪性强，计算量小，实现较为简单。

[1] 林海雪(Lin Haixue).电力系统中的间谐波问题(Interharmonics in electrical power system)[J].供用电(Distribution amp; Utilization)，2001，18(3)：6-9.

[2] 郝江涛，刘念，幸晋渝，等(Hao Jiangtao, Liu Nian, Xing Jinyu,etal).电力系统间谐波分析(Study on interharmonic of power system)[J].电力自动化设备(Electric Power Automation Equipment)，2004，24(12)：36-39.

[3] 祁才君，王小海(Qi Caijun, Wang Xiaohai).基于插值FFT算法的间谐波参数估计(Interharmonics estimation based on interpolation FFT algorithm)[J].电工技术学报(Transactions of China Electrotechnical Society)，2003，18(1)：92-95.

[4] 薛蕙，杨仁刚(Xue Hui，Yang Rengang). 利用Morlet连续小波变换实现非整次谐波的检测(Morlet wavelet based detection of noninteger harmonics)[J].电网技术(Power System Technology)，2002，26(12)： 41-44.

[5] 王小华，何怡刚(Wang Xiaohua, He Yigang).一种新的基于神经网络的高精度电力系统谐波分析算法(A new neural network based power system harmonics analysis algorithm with high accuracy)[J].电网技术(Power System Technology)，2005，29(3)：72-75.

[6] 聂永辉，刘彦臣，张立艳(Nie Yonghui, Liu Yanchen, Zhang Liyan).TLS-ESPRIT技术在电力系统谐波检测的应用(Application of TLS-ESPRIT on harmonic measurement of power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010，22(2)：129-133.

[7] 张君俊,杨洪耕(Zhang Junjun, Yang Honggeng).间谐波参数估计的TLS-ESPRIT算法(TLS-ESPRIT for interharmonic estimation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2010，22(2)： 70-75.

[8] 王志群，朱守真，周双喜(Wang Zhiqun, Zhu Shouzhen, Zhou Shuangxi). 基于Pisarenko谐波分解的间谐波估算方法(Inter-harmonics estimation by Pisarenko harmonic decomposition method)[J].电网技术(Power System Technology)，2004， 28(15)：72-77,82.

[9] 丁屹峰，程浩忠，吕干云，等(Ding Yifeng, Cheng Haozhong, Lü Ganyun,etal).基于Prony算法的谐波和间谐波频谱估计(Spectrum estimation of harmonics and interharmonics based on Prony algorithm)[J].电工技术学报(Transactions of China Electrotechnical Society)，2005，20(10)：94-97.

[10]武艳华，黄纯，邢耀广，等(Wu Yanhua, Huang Chun, Xing Yaoguang,etal).基于AR模型的间谐波检测算法的研究(Interharmonics measuring algorithm based on AR model spectral estimation)[J].继电器(Relay)， 2006，34(2)：41-45,52.

[11]石敏，吴正国，尹为民(Shi Min, Wu Zhengguo, Yin Weimin).基于多信号分类法和普罗尼法的间谐波参数估计(Inter-harmonics parameter estimation based on multi-signal classification and Prony method )[J].电网技术(Power System Technology)，2005，29(15)：81-84.

[12]邓乃扬，田英杰. 支持向量机：理论、算法与拓展[M].北京：科学出版社，2009.

[13]占勇，丁屹峰，程浩忠，等(Zhan Yong, Ding Yifeng, Cheng Haozhong,etal).电力系统谐波分析的稳健支持向量机方法研究(A robust support vector algorithm for harmonics analysis of electric power system)[J].中国电机工程学报(Proceedings of the CSEE)，2004，24( 12)： 43-47.

[14](美)Dimitris G M，Vinay K I， Stephen M K.统计与自适应信号处理[M].周正，顾仲梅译. 北京: 电子工业出版社, 2003.

[15]刘开培，周莉，马秉伟(Liu Kaipei, Zhou Li, Ma Bingwei).基于支持向量机的间谐波检测及其在LabVIEW平台的实现(Interharmonic detection based on regressive type of support vector machine and its realization on platform of LabVIEW)[J].电网技术(Power System Technology)，2006，30(5)：76-80.

[16]程浩忠，艾芊， 张志刚，等. 电能质量[M].北京：清华大学出版社，2006.

[17]Leonowicz Zbigniew, Lobos Tadeusz, Rezmer Jacek. Advanced spectrum estimation methods for signal analysis in power electronics [J]. IEEE Trans on Industrial Electronics, 2003, 50(3):514-519.

李 新(1960-)，女，教授，博士生导师，研究方向为电力系统信号处理，电气设备故障的智能化诊断技术，电能质量等。Email:lltd@cqu.edu.cn

陈文礼(1986-)，男，硕士研究生，研究方向为电能质量及电能计量。Email:wenlicqu@126.com

侯兴哲(1966-)，男，高级工程师，研究方向为电力测试及电能计量管理。Email:hxz@cqet.com

付志红(1966-)，男，教授，博士生导师，研究方向为电力电子、电磁探测技术。Email:fuzhihong@cqu.edu.cn

InterharmonicsEstimationUsingSVMandTLS-ESPRIT

LI Xin1， CHEN Wen-li1， HOU Xing-zhe2， FU Zhi-hong1， SU Xiang-feng1

(1.State Key Laboratory of Power Transmission Equipment amp; System Security and New Technology, Chongqing University, Chongqing 400044, China；2.Chongqing Electric Power Test amp; Research Institute, Chongqing 401123, China)

To accurately estimate the interharmonics parameters, a method by using support vector machine (SVM) and total least square-estimation of signal parameters via rotational invariance techniques (TLS-ESPRIT) is proposed. First, the singular value decomposition (SVD) was used to HANKEL matrix constructed by sampling data, and the total least square (TLS) was used to solve the rotation equation for estimating frequency components of signals; Then the SVM was used to estimate the amplitude values and the phases of signals. The simulation results indicate that the method can effectively estimate all interharmonics parameters, which not only reduce the computation quantity with only using SVM, but also exhibit robustness characteristics in low SNR.

interharmonics； singular value decomposition； total least square-estimation of signal parameters via rotational invariance techniques； support vector machine(SVM)； robustness

TM935

A

1003-8930(2012)02-0067-05

2011-03-08；

2011-04-01

输配电装备及系统安全与新技术国家重点实验室自主研究项目(2007DA10512709209)；重庆大学“211工程”三期创新人才培养计划建设项目(S-09111)